1.树的概念(一对多)(要求会写遍历序列)
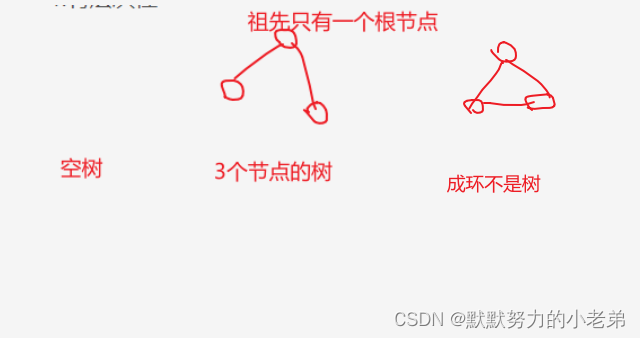
1)n>=个节点,n=0时为空树
2)仅有一个根节点
3)左右节点互不相交,子节点一对多
2.树的特点
1.子树之间没有关系
2.节点不属于多个子树(一个节点只能在一颗子树里面)
3.没有回路(就是成环)
4.有层次性
3.术语
1.节点的度:拥有子树的个数
树的度: 求最大值 max(树各节点的度)
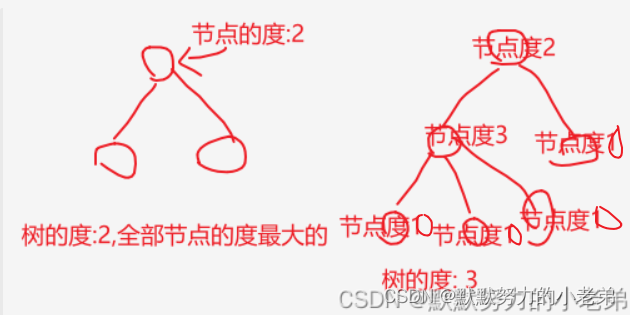
2.叶子节点(终端节点) 度=0
分支节点 (非终端节点) 度!=0

3.孩子 双亲(父节点) 兄弟 祖先(下面都是子孙)
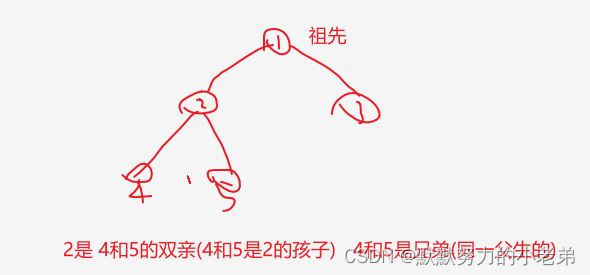
4.路径(从上到下)
1)路径长度=经过边数-1
2) 路是唯一的(父是唯一的)
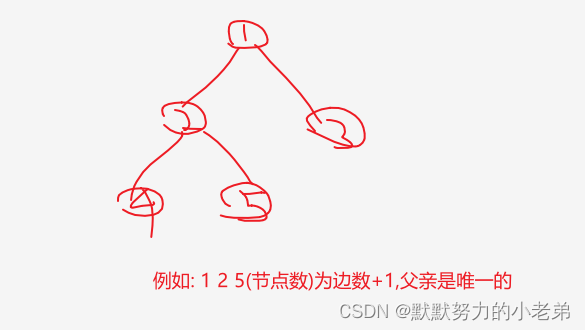
5.节点所在层数
1)深度/高度(上下的最大节点数)
2)宽度(一层的左右的最大节点数)
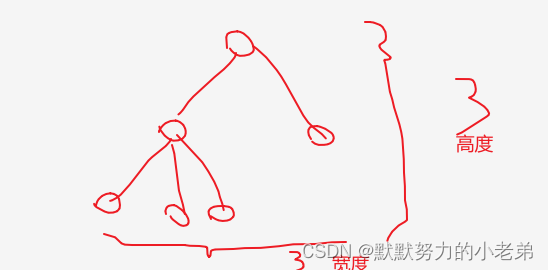
3.树的遍历(对全部元素访问一遍)(没有遗漏,没有重复的访问)(从根开始访问一某种次序)(根节点在哪个位置就叫做x序遍历)
1.前序遍历(递归)(先访问根节点,后访问左节点到右节点)
2.后序遍历(递归)(先访问左节点到右节点,再访问根节点)
3.层序遍历(一层一层访问)
例如:
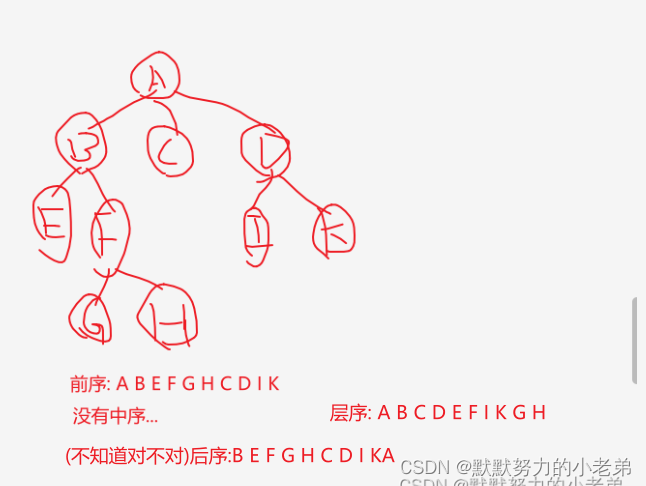
4.树的存储结构(数据元素+逻辑关系)
1.双亲表示法 (层序存储) 查双亲O(1) 查孩子O(n)查整个表,需要+firstChild优化+孩子数为O(1)
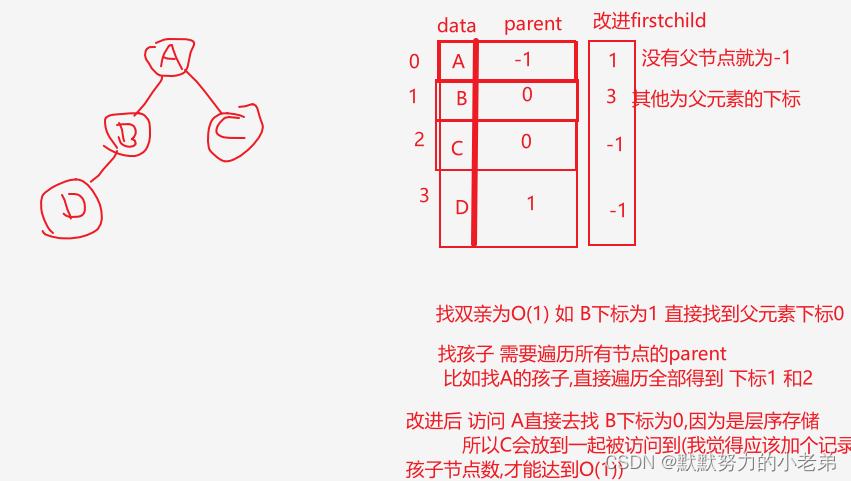
2.孩子表示法
1.方案1: 指针域个数=树的度(会浪费,大量的没有指向的指针) 2.方案2: 指针域个数=节点数的度(不浪费,但是节点结构不一样) 3.方案3: 数组+指针(实用) 查孩子O(1) 查双亲O(n) +parent数组优化到O(1)
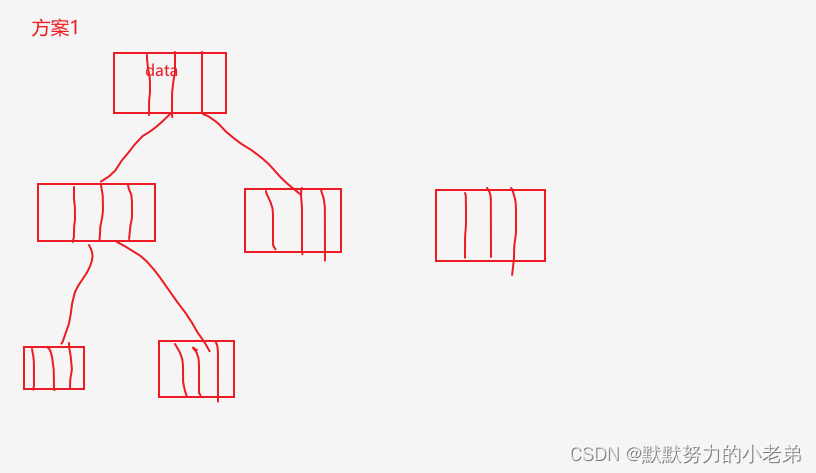
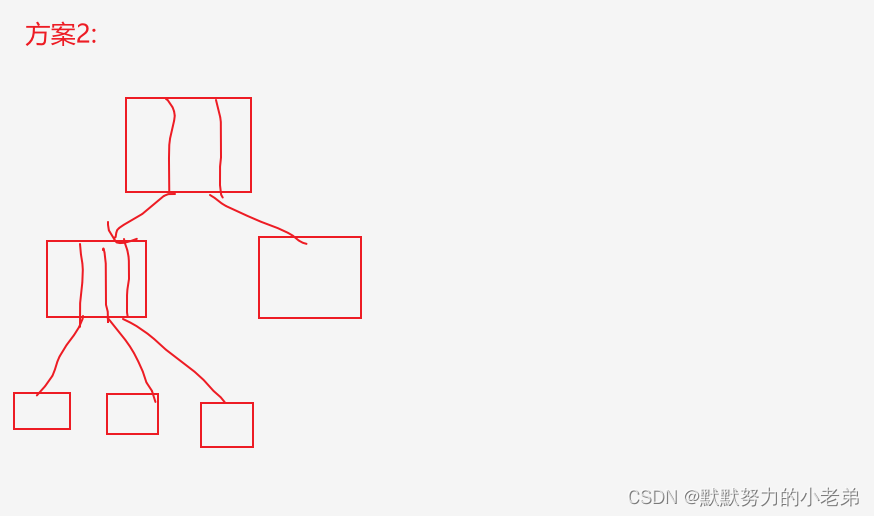
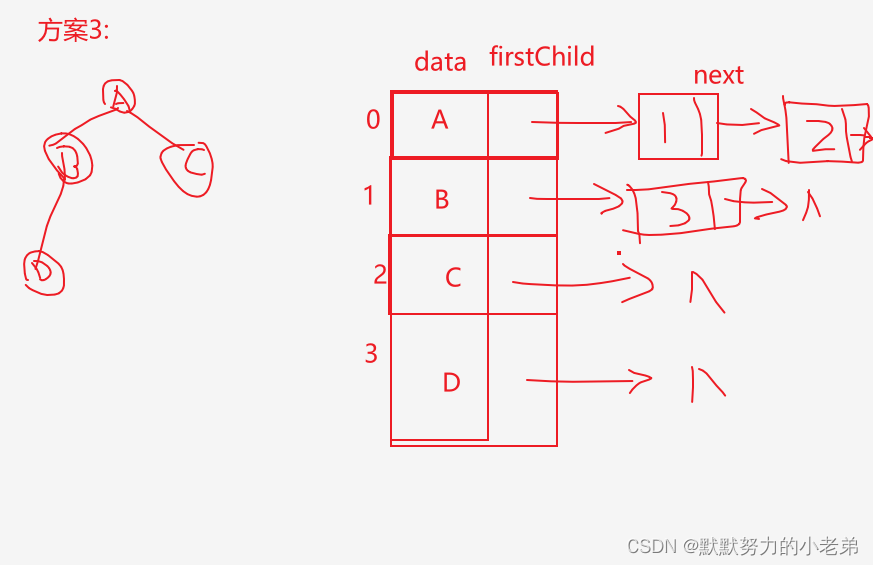
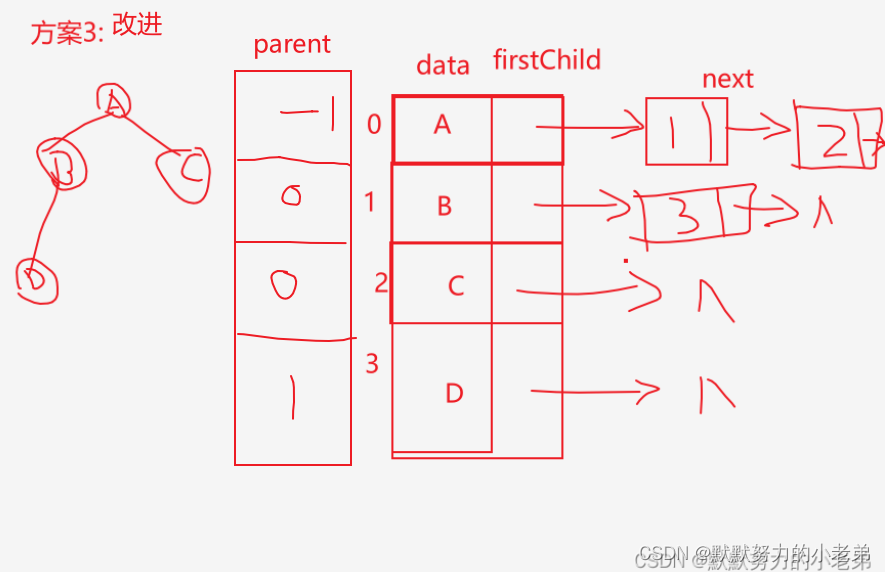
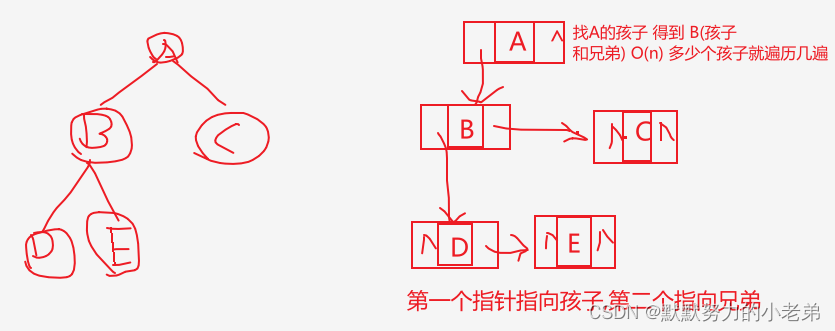
3.孩子兄弟表示法(可以找孩子和兄弟)(指针指向孩子和兄弟) 找兄弟O(1) 找孩子O(n)
5.二叉树(考遍历序列和画树)?
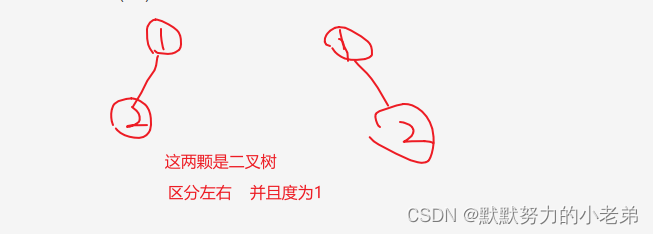
1.存在空二叉树,两颗互不相交的左右子树,区分左右子树
2.二叉树不是度为2的树(对)
3.度下于等于2(错) 可能不为2
4.斜树 左斜树:只有左边的节点;右斜树:只有右边的节点 高度==节点数(一层一个节点)

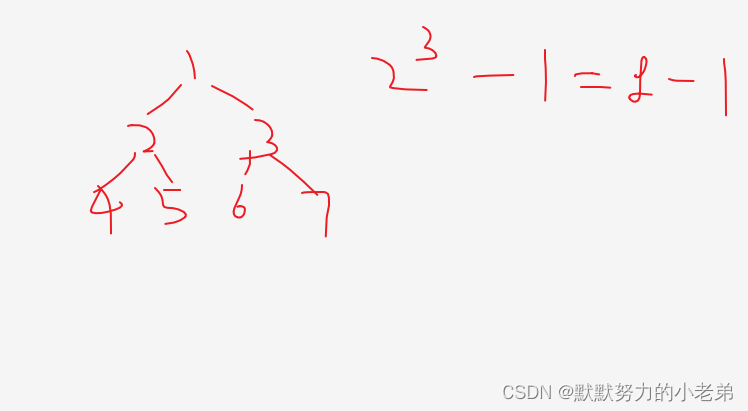
6.满二叉树
特点:
1.叶子在最后一层
2.只有度= 0或2
3.同深度二叉树,他的叶子最多
4.节点数 = 2^(i) -1 (i>=0) i是层树
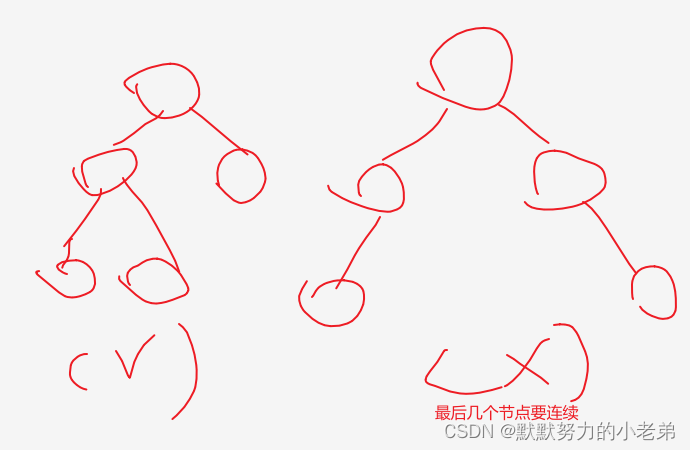
 7.完全二叉树(满二叉树去最后几个节点[必须是连续的n个节点])
7.完全二叉树(满二叉树去最后几个节点[必须是连续的n个节点])
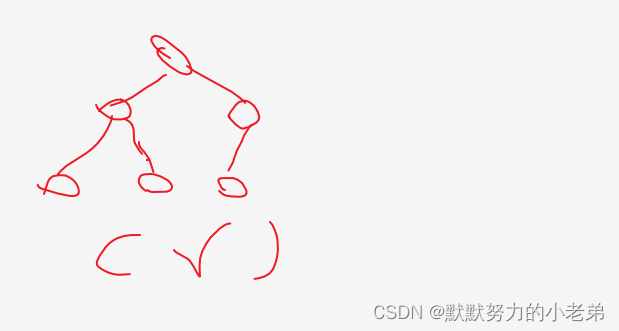
8.二叉树的性质
- 如果节点度=1 一定只有一个左孩子
- 度 n0=n2+1;(叶子节点数=度为2 +1)
证明: n=n0+n1+n2; (全部度相加=节点数)
n=n1+2n2+1;(边数+1=节点数)- 二叉树 第i层最多有 2^(i-1)个节点
- 深度=k 最多2^k -1 个节点 !!!
- n个节点的完全二叉树 深度=|Log2n|+1(||代表向下取整)
- 双亲序号 i/2 (i>1)
i的左孩子 2i (2i<=n)
右 2i+1 (2i+1,=n)
9.二叉树的遍历(限定先左后右)
- 层序遍历(之前说过了,就不重复了)
- 前,中,后序遍历
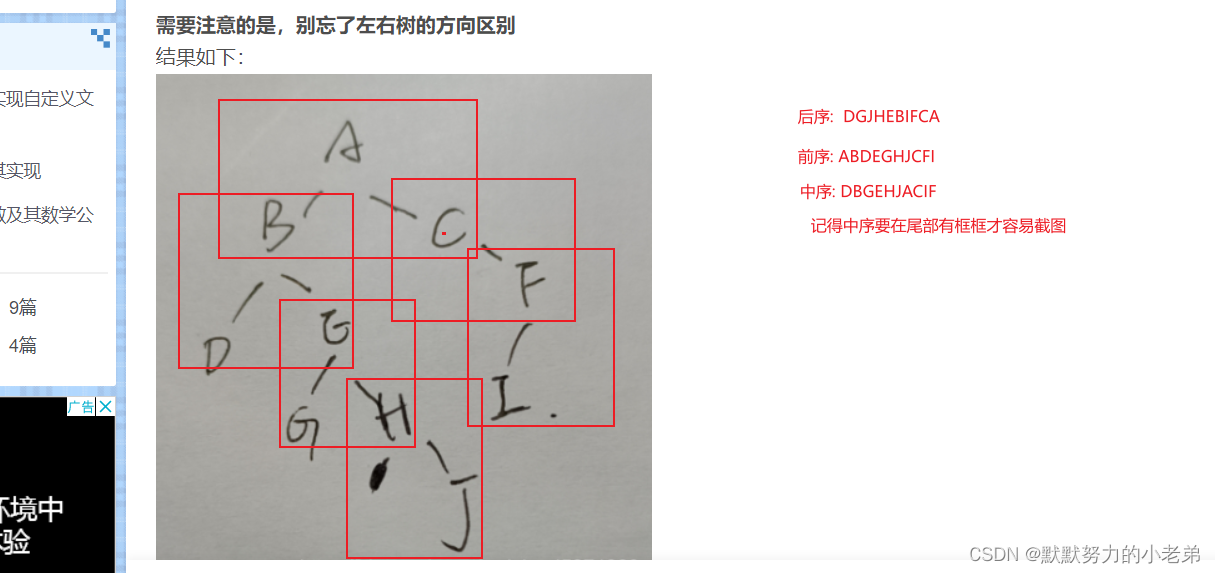
- 给一个前/中/后序列不能得到 二叉树,需要 中序+其他序 才可以 , 没有中序则不能得到二叉树
- 例子:

全部使用框框(从根开始)才容易解题.
10.二叉树c语言代码
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define MaxSize 100
/*将二叉链表的结点结构定义和各个函数定义放到这里*/
typedef char DataType; /*定义二叉树结点的数据类型,假设为char型*/
typedef struct BiNode { /*定义二叉链表的结点类型*/
DataType data;
struct BiNode *lchild, *rchild;
} BiNode;
void PreOrder(BiNode *root) { //前序遍历
if (root == NULL) return; /*递归调用的结束条件*/
else {
printf("%c ", root->data); /*访问根结点的数据域,为char型*/
PreOrder(root->lchild); /*前序递归遍历root的左子树*/
PreOrder(root->rchild); /*前序递归遍历root的右子树*/
}
}
void InOrder (BiNode *root) { //中序遍历
if (root == NULL) return; /*递归调用的结束条件*/
else {
InOrder(root->lchild); /*中序递归遍历root的左子树*/
printf("%c ", root->data); /*访问根结点的数据域,为char型*/
InOrder(root->rchild); /*中序递归遍历root的右子树*/
}
}
void PostOrder(BiNode *root) {//后序遍历
if (root == NULL) return; /*递归调用的结束条件*/
else {
PostOrder(root->lchild); /*后序递归遍历root的左子树*/
PostOrder(root->rchild); /*后序递归遍历root的右子树*/
printf("%c ",root->data); /*访问根结点的数据域,为char型*/
}
}
void LeverOrder(BiNode *root) {//层序遍历
int rear;
BiNode *q = NULL, *Q[MaxSize]; /*采用顺序队列*/
//等同于定义了一个二叉树结构的队列 BiNode *Q[MaxSize];
int front = rear = -1; /*初始化顺序队列*/
if (root == NULL) return; /*二叉树为空,算法结束*/
Q[++rear] = root; /*根指针入队*/
while (front != rear) { /*当队列非空时*/
q = Q[++front]; /*出队*/
printf("%c ", q->data); /*访问结点,为char型*/
if (q->lchild != NULL) Q[++rear] = q->lchild;
if (q->rchild != NULL) Q[++rear] = q->rchild;
}
}
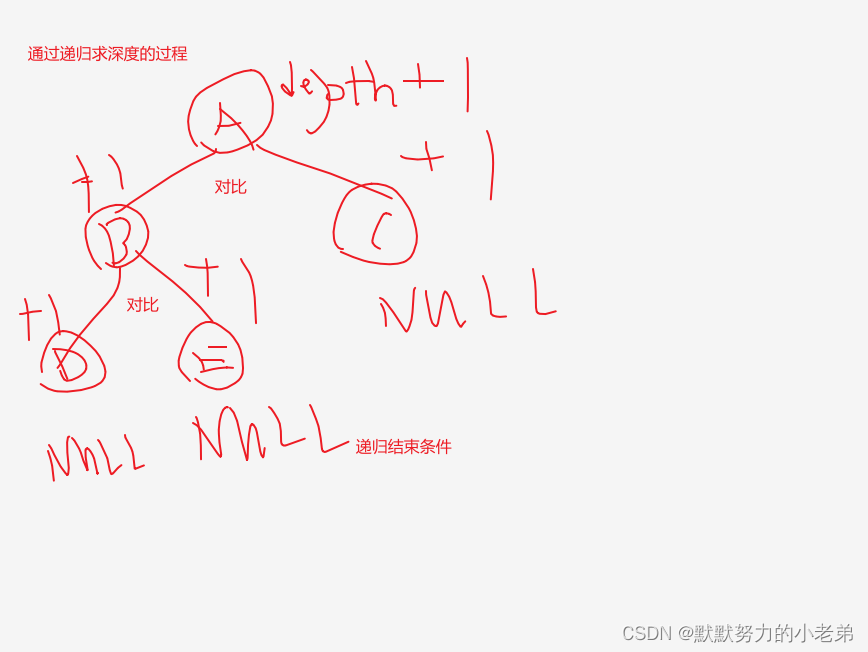
int CalDepth(BiNode *root, int depth) { //得到二叉树的深度
if (root == NULL) return depth; /*递归调用的结束条件*/
else {
int left_depth = CalDepth(root->lchild, depth + 1);
int right_depth = CalDepth(root->rchild, depth + 1);
return left_depth > right_depth ? left_depth : right_depth;
}
}
int CalNodeNumber(BiNode *root){ //递归求全部节点数
if(root == NULL) return 0;
int count = 1;
count += CalNodeNumber(root->lchild);
count += CalNodeNumber(root->rchild);
return count;
}
int CalLeafNumber(BiNode *root){//计算叶子节点数量
if(root == NULL) return 0;
int count = 0;
if(root->lchild == NULL && root->rchild == NULL) count = 1; //到空的时候才判断是叶子节点
count += CalLeafNumber(root->lchild);
count += CalLeafNumber(root->rchild);
return count;
}
BiNode * CreatBiTree(BiNode *root) {
char ch;
scanf("%c", &ch); /*输入结点的数据信息*/
if (ch == '#' || ch == '\n') root = NULL; /*递归结束,建立一棵空树*/
else {
root = (BiNode *)malloc(sizeof(BiNode)); /*生成新结点*/
root->data = ch; /*新结点的数据域为ch*/
printf("建立结点%c\n建立结点%c的左子树\n",ch,ch);
root->lchild = CreatBiTree(root->lchild); /*递归建立左子树*/
printf("结点%c左子树建立完毕,建立其右子树\n",ch);
root->rchild = CreatBiTree(root->rchild); /*递归建立右子树*/
printf("结点%c的右子树建立完毕\n",ch);
}
return root;
}
void DestroyBiTree(BiNode *root) {
if (root == NULL) return;
DestroyBiTree(root->lchild);
DestroyBiTree(root->rchild);
free(root);
}
int main( ) {
BiNode *root = NULL; /*定义二叉树的根指针变量*/
printf("开始建立二叉树,请输入建立序列\n");
root = CreatBiTree(root); /*建立一棵二叉树*/
printf("二叉树建立完毕\n");
int depth = CalDepth(root, 0);
printf("二叉树的深度是: %d\n", depth);
int count = CalNodeNumber(root);
printf("二叉树的结点数为:%d\n", count);
int leaf = CalLeafNumber(root);
printf("二叉树的叶子节点数为:%d\n", leaf);
printf("该二叉树的根结点是:%c\n", root->data);
printf("\n该二叉树的前序遍历序列是:");
PreOrder(root);
printf("\n该二叉树的中序遍历序列是:");
InOrder(root);
printf("\n该二叉树的后序遍历序列是:");
PostOrder(root);
printf("\n该二叉树的层序遍历序列是:");
LeverOrder(root);
DestroyBiTree(root);
return 0;
}
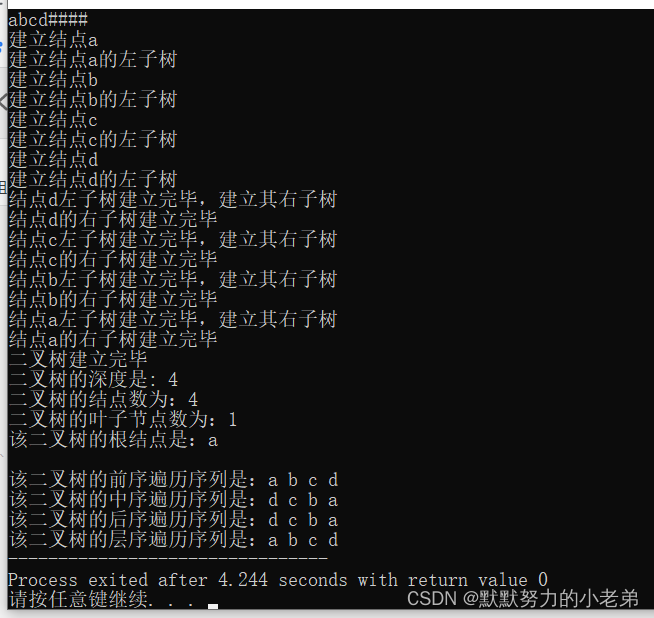
运行截图