题目描述

一个字符串的前缀是从第一个字符开始的连续若干个字符，例如 abaab 共有 $5$ 个前缀，分别是 a，ab，aba，abaa，abaab。

我们希望知道一个 $N$ 位字符串 $S$ 的前缀是否具有循环节。

换言之，对于每一个从头开始的长度为 $i$（$i>1$）的前缀，是否由重复出现的子串 $A$ 组成，即 $AAA\dots A$ （$A$ 重复出现 $K$ 次,$K>1$）。

如果存在，请找出最短的循环节对应的 $K$ 值（也就是这个前缀串的所有可能重复节中，最大的 $K$ 值）。

输入格式

输入包括多组测试数据，每组测试数据包括两行。

第一行输入字符串 $S$ 的长度 $N$。

第二行输入字符串 $S$。

输入数据以只包括一个 $0$ 的行作为结尾。

输出格式

对于每组测试数据，第一行输出 Test case # 和测试数据的编号。

接下来的每一行，输出具有循环节的前缀的长度 $i$ 和其对应 $K$，中间用一个空格隔开。

前缀长度需要升序排列。

在每组测试数据的最后输出一个空行。

数据范围

$2\le N\le 1000000$

输入样例：

3
aaa
4
abcd
12
aabaabaabaab
0

输出样例：

Test case #1
2 2
3 3

Test case #2

Test case #3
2 2
6 2
9 3
12 4

---

题意重述

编写一个程序，对于每一个前缀子串 $s_i$，找出它的最短循环节的重复次数。$s_i$ 的最短循环节是指连续组合能恰好构成 $s_i$ 的最短的子串。例如，对于字符串 “aabaabaa”，“aab” 不是其最短循环节，因为它无法恰好构成原串。

注意，在以下叙述中，下标从1开始。

算法

通过KMP算法可以求得next数组，对于每一个前缀子串 $s_i$，其最短循环节的长度就是 $i-\text{next}[s_i]$。
为什么呢？

首先看图，上下两条线表示同一个字符串，重合的部分表示KMP匹配(前后缀相等的最大长度)。
上面的1就是下面的1(完全相同的部分)，而下面的1等于上面的2(前后缀匹配)，上面的2等于下面的2，而下面的2等于上面的3…
所以上面的1，2，3，4，5和下面的1，2，3，4，5完全相同。

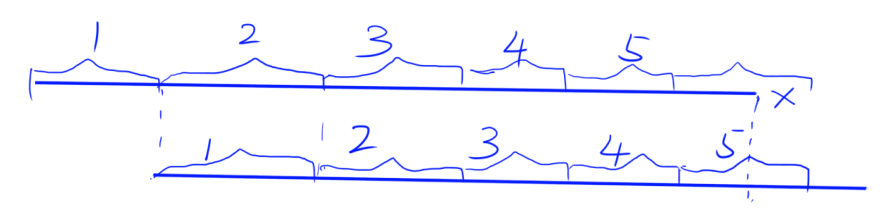
在不严格要求“恰好”构成时，每一小段都可以视作原串的循环节。然后，我们可以证明，这样的小段就是原串的最短循环节。
那么，如何证明呢？

反证: 假设该小段字符串T不是最短循环节，则原串中必然存在T’作为最短循环节。那么对于T’,可以按照上图的方式，将上下两串划分为一个个由T’组成的部分。

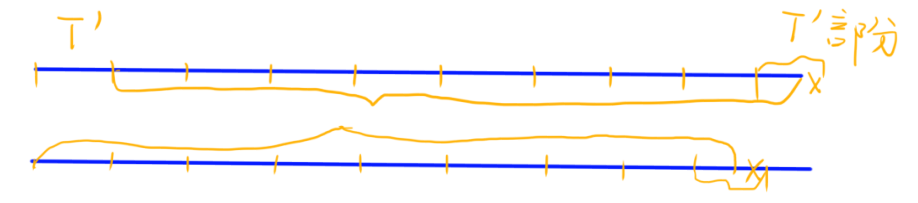
此时矛盾出现:如果可以用更小的T’划分，则根据图示，原串的KMP匹配长度就是 $n-\text{len}(T^{\prime })$。这个长度 $n-\text{len}(T^{\prime })$ 超过了 $n-\text{len}(T)$，而 $n-\text{len}(T)$ 是原串的最大前后缀匹配长度。所以假设是错误的，也就是说，T确实是最短循环节。

当不严格要求“恰好”构成时，$n-\text{len}(T)=n-\text{next}[n]$ 就是最短循环节的长度。对于每一个前缀子串 $s_i$，其最短循环节的长度就是 $i-\text{next}[i]$。那么，当我们严格要求恰好构成时，又会是怎样呢？

我们可以证明一个引理，一个字符串的任何循环节（除最短循环节外）都是最短循环节的倍数。也就是说，不存在其他可能的模式使得原串能够恰好由其循环构成。因此，如果原串长度能被 $len(T)$ 整除，则存在最短循环节且为 $s[1\sim len(T)]$，如果不能被整除，则不存在（按题目的要求，不能“恰好”构成就是为不存在）。

引理证明:

反证: 假设原串存在一个子串T’,它不是最短循环节，也不是最短循环节的循环构成(倍数)，但是可以循环构成原串。(有点绕)

这就意味着 $len(T^{\prime })>len(T)$，且 $len(T^{\prime })$ 不是 $len(T)$ 的倍数。根据循环节的定义，T 和 T’ 都可以构成原串。即原串可以写为 $TT...TA$（T出现 m 次）或 $T^{\prime }{T}^{\prime }...T^{\prime }B$（T’出现 n 次）。这里的 A 和 B 可能是空串，或者长度不足一个 T 或 T’ 的部分。满足 $m\times len(T)=n\times len(T^{\prime })$。

于是我们可以找到一个更小的循环节，其长度为d，因为
$$s_j=s_{j+len(T)}=s_{j+2len(T)}=\cdots =s_{j+xlen(T)}=s_{j+xlen(T)-len(T^{\prime })}=s_{j+xlen(T)-2len(T^{\prime })}=\cdots =s_{j+xlen(T)-ylen(T^{\prime })}=s_{j+d}$$

此处的 $j$ 可以从几乎任意位置开始，只要字符串的长度足够长以支持所描述的周期 (如果不支持，那么表示从j开始的后续部分无法使用T’进行重复构成，这样的情况则不需要讨论。)。

但这与T是最短循环节的假设产生矛盾，假设不成立。故不存在一种循环节使得它既不是最短循环节，也不是最短循环节的倍数。

看明白了，请给我点赞，谢谢(*^▽^*)。

时间复杂度 $\mathcal{O}(n)$

KMP+线性扫描，$\mathcal{O}(n)$。

C++ 代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e6 + 10;
char s[N]; int ne[N];

int main(){
    int T = 1;
    int n;
    while(scanf("%d", &n), n){
        printf("Test case #%d\n", T ++);
        scanf("%s", s + 1);
        
        for(int i = 2, j = 0; i <= n; ++ i){
            while(j && s[i] != s[j + 1]) j = ne[j];
            if(s[i] == s[j + 1]) j ++;
            ne[i] = j;
        }
        
        for(int i = 1; i <= n; ++ i){
            int t = i - ne[i];
            if(i > t && i % t == 0){  // i>t保证循环节至少出现2次
                printf("%d %d\n", i, i / t);
            }
        }
        puts("");
    }
}