一、中介效应说明
中介效应主要研究自变量对因变量影响的过程中,自变量是否通过中介变量再对因变量产生影响,那什么情况表明中介效应存在呢?如果自变量对因变量影响过程中,中介变量在模型中有着桥梁般的作用,那说明中介效应存在。比如在电商数据中,经济发展水平通过影响居民收入从而影响电子商务。模型如下:

二、中介效应常见类型
中介效应常见有两种类型,一种是平行中介一种是链式中介,平行中介:一般是指多个中介变量在自变量对因变量的影响中起着同等重要的作用,中介变量之间互不影响,比如经济发展水平通过影响居民收入从而影响电子商务,经济发展水平还可以通过影响消费能力进而影响电子商务,则模型一般如下:

链式中介:一般指几个中介变量在自变量对因变量的影响中起着一样的中介作用,到那时中介变量之间相互影响,一般模型如下:

三、数据类型及操作
一般数据有两种类型一个是定类变量一个是定量变量,通常中介作用的中介变量和自变量均为定量变量,如果自变量为定类变量怎么办?可以将自变量进行哑变量处理,处理后需要在分析时少放入一项作为参考项。进行中介效应分析,可以使用SPSSAU中的中介作用进行分析,或者使用分层回归进行研究。
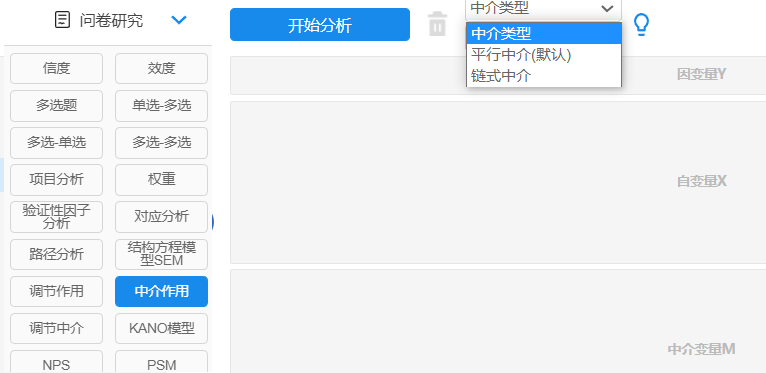
中介作用:
分层回归分析:

四、分析中常见步骤
1、数据处理
此步骤通常是对自变量、因变量、中介变量做标准化处理,有时也使用中心化处理。标准化处理和中心化处理的主要目的是为了减少多重共线性。此步骤可以在SPSSAU中数据处理模块的生成变量进行处理,有时研究者的变量是由多个题项组成,而中介作用并不是对题项进行研究而是对变量进行研究,所以需要先进行计算对应题项的平均得分,并以平均得分代表对应的变量。比如幸福感变量由3个题项表述,则应该计算3个题项的平均分进行表示该变量。
2、分析第一个模型
第一个模型针对自变量对因变量的回归关系进行分析。比如例子中的经济发展水平对电子商务的影响,一般称为总效应,其模型公式一般为:Y=cX+e1(其中c代表自变量对因变量的回归系数,e1代表残差);

3、分析第二个模型
第二个模型是在第一个模型基础上加入中介变量,也就是自变量和中介变量对因变量分层回归。其模型公式一般为:Y=c’X+bM+e2(c’代表此模型中X对Y的回归系数一般称为直接效应,b代表M对Y的回归系数,e2代表此模型的残差);

4、分析第三个模型
第三个模型为自变量对中介变量的回归分析,其一般式为M=aX+e3(a代表X对M的回归系数,e3代表残差);

5、进行中介效应分析
(1)最后进行中介效应分析,首先查看第一个模型的系数c如果不显著,则说明自变量对因变量没有影响,如果显著说明自变量对因变量有影响,进一步分析。
(2)然后进行查看模型2的系数b和模型3的系数a,如果a和b均显著,则查看模型3的系数c’, c’显著则为部分中介,c’不显著则为完全中介。
(3)如果a和b至少一个不显著,则进行sobel检验,sobel检验显著则为部分中介,如果sobel检验不显著则没有中介作用。(sobel检验请参考:http://quantpsy.org/sobel/sobel.htm)
此种方法简单易懂,、容易理解和解释,因而受到广泛的应用,但有学者认为其检验效能较低,有时候本身有中介作用但却显示没有中介作用。因为有学者将检验流程进行优化:
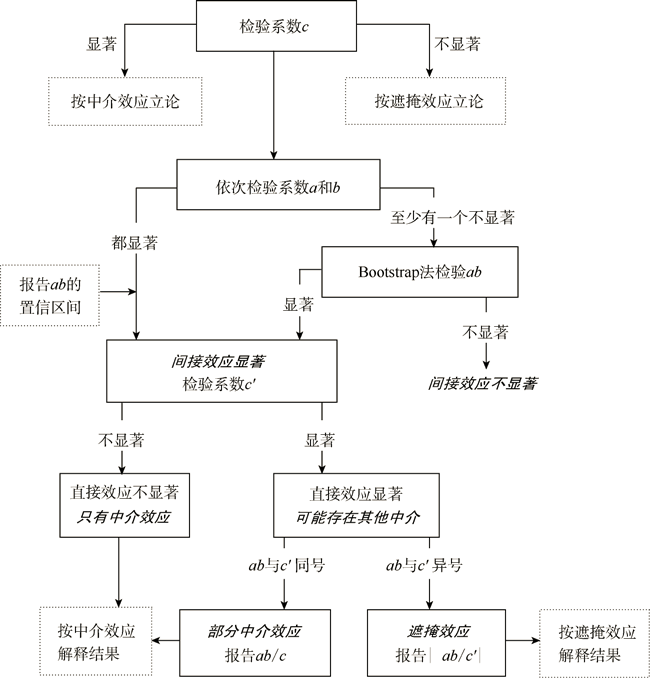
图表解说:
上图中回归系数a和回归系数b的乘积项(a*b)称为间接效应,如果其呈现出显著性,那么就说明具有中介作用,反之不具有显著性,则说明不具有中介作用。检验a*b的显著性用于判断是否具有中介作用,这种做法即称为乘积系数检验法。而具体Bootstrap抽样法检验是指a*b这个回归系数的95%置信区间是否包括数字0;如果说95%置信区间不包括数字0,则说明具有中介作用;如果说95%置信区间包括数字0,即说明没有中介作用。所以具体说明如下:
第一:c表示X对Y时的回归系数(模型中没有中介变量M时),即总效应;
第二:a表示X对M时的回归系数,b表示M对Y时的回归系数,a*b为a与b的乘积即中介效应;
第三:95% BootCI表示Bootstrap抽样计算得到的95%置信区间,如果区间不包括0则说明显著;
第四:c’表示X对Y时的回归系数(模型中有中介变量M时),即直接效应;
第五:如果a和b显著,且c’不显著,则为完全中介;
第六:如果a和b显著,且c’显著,且a*b与c’同号,则为部分中介作用;
第七:如果a和b显著,且c’显著,且a*b与c’异号,则为遮掩作用;
第八:如果a和b至少一个不显著,且a*b的95% BootCI包括数字0(不显著),则中介作用不显著;
第九:如果a和b至少一个不显著,且a*b的95% BootCI不包括数字0(显著),且c’不显著,则为完全中介;
第十:如果a和b至少一个不显著,且a*b的95% BootCI不包括数字0(显著),且c’显著,且a*b与c’同号,则为部分中介作用;
第十一:如果a和b至少一个不显著,且a*b的95% BootCI不包括数字0(显著),且c’显著,且a*b与c’异号,则为遮掩作用;
五、中介效应分析
接下来举例进行分析中介效应,以进行优化过得流程为参考。案例背景:某公司想要研究个人发展、工作特性、工作回报是否通过团队合作对创新绩效产生影响。其中个人发展、工作特性、工作回报为自变量,团队合作为中介变量,创新绩效为因变量。操作如下:

结果如下:
首先查看中介作用的三个模型以及系数,如下表:
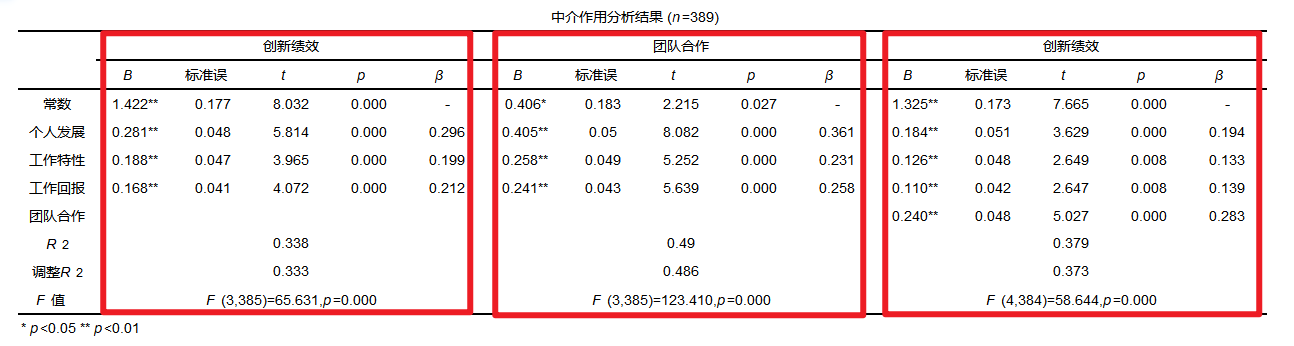
从上表可知:中介效应分析共涉及3个模型,分别如下:
创新绩效=1.422+0.281*个人发展+0.188*工作特性+0.168*工作回报
团队合作=0.406+0.405*个人发展+0.258*工作特性+0.241*工作回报
创新绩效=1.325+0.184*个人发展+0.126*工作特性+0.110*工作回报+0.240*团队合作
接下来查看中介效应的结果,如下表:

- 个人发展→团队合作→创新绩效
上表得知总效应c显著,并且系数a和系数b均显著,且与c’同号(都大于0)则为部分中介。 - 工作特性→团队合作→创新绩效
上表得知总效应c显著,并且系数a和系数b均显著,且与c’同号(都大于0)则为部分中介。 - 工作回报→团队合作→创新绩效
上表得知总效应c显著,并且系数a和系数b均显著,且与c’同号(都大于0)则为部分中介。
得到的中介效应量如下:
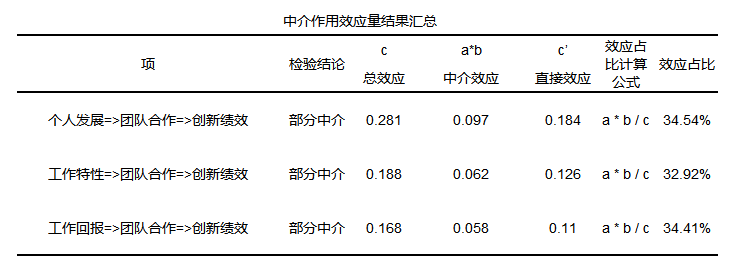
效应量计算说明如果是完全中介,则效应占比为100%,如果是部分中介,则效应占比计算公式为:a*b/c,如果是遮掩效应,则效应量为中介效应与直接效应的比值,计算公式为:| a*b/c |。
六、疑难解惑
1.95%区间包括0,为什么显示有中介作用?
中介作用分析有着非常严格的检验流程,绝大多数情况下,95%抽样区间不包括数字0就意味着具有中介作用,但并不完全是这样,最终中介作用的检验需要参考检验流程进行。
2. 面板数据是否可以进行中介作用?
从数学理论上,面板数据可以直接进行中介作用分析,中介作用分析并不区分是否面板数据,直接分析即可。
3.间接效应和中介效应的区别是什么?
通常情况下二者意义完全一致,但细微区别在于比如X->M1->M2->Y这种链式中介时,一般用间接效应描述会更易理解。