1.二叉树

先、中、后序遍历
先序（中、左、右）：1，2，4，5，3，6，7
中序（左、中、右）：4，2，5，1，6，3，7
后序（左、右、中）：4，5，2，6，7，3，1

void f(Node head)
{
   if(head==null)
      {return;}
   f(head.left);
   f(head.right);

}
//先序遍历(中、左、右）
void preOrderRecur(Node head)
{
    if(head==null){
       return;
 }
      cout<<head.value<<endl;
      preOrderRecur(head.left);
      preOrderRecur(head.right);
}
//中序遍历(左、中、右）
void InOrderRecur(Node head)
{
    if(head==null){
       return;
 }     
      InOrderRecur(head.left);
      cout<<head.value<<endl;
      InOrderRecur(head.right);
}
//后序遍历(左、右、中）
void PosOrderRecur(Node head)
{
    if(head==null){
       return;
 }
     
      PosOrderRecur(head.left);
      PosOrderRecur(head.right);
      cout<<head.value<<endl;
}

1，2，4，4，4，2，5，5，5，2，1，3，6，6，6，3，7，7，7，3，1
先序：打印第一次遇到
中序：打印第二次遇到
后序：打印第三次遇到

void inorderunrecur(node head)
{
    if(head!=null)
    stack<node> stack= new stack<node>():
    node cur=head;
    while(!stack.isEmpty()||cur!=null)
    {
      if(cur!=null)
      {
           stack.push(cur); //1.进栈
           cur=cur.left; 
     }
    else
    {
       cur= stack.pop();//2.栈中弹出
       cur= cur.right;  //3.右子树弹出
    }
}

打印二叉树
二叉树的宽度优先遍历

void process(Node head)
{
    if(head==null)
    {
      return;
    }
     Queue<Node> queue= new LinkedList<>();//创建双向链表
     queue.add(head);
     while(!queue.isEmpty())   //如果队列不为空
     {
       Node cur=queue.poll();   //弹出就打印
       count<<cur.value<<endl;
       if(cur.left!=null)       //有左孩子
       {
          queue.add(cur.left);
       }
       if(cur.right!=null)      //有右孩子
       {
          queue.add(cur.right);
       }
     }

}

void main()
{
 
   process(head);
}

怎么求一个二叉树的最大宽度

//1.构造树

          1
   2            3
4    5        6   7
       8    9       10

void main(String[] args) {
		Node head = new Node(1);
		head.left = new Node(2);
        head.right = new Node(3);
		head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        head.right.right = new Node(7);
		head.left.right.right = new Node(8);
        head.right.left.left = new Node(9);
        head.right.riht.right = new Node(10);

	    process(head);
	}

添加节点的层数：

void process(Node head)
{
    if(head==null)
    {
      return;
    }
     

     HashMap<Node,Int> levelMap = new HashMap<>; //层数表   


     Queue<Node> queue= new LinkedList<>();     //创建双向链表

     levelMap.put(head,1);
     queue.add(head);

     int clevel=1; //当前层数
     int cnodes=0; //每层的个数
     int max=0;    //最大值


     while(!queue.isEmpty())    
     {
       Node cur=queue.poll();          //弹出就打印
       
       int level=levelMap.get(cur)
       if(level==clevel)
       {
             cnodes++;
       }
       else
       {
          if(cnodes>max)
          {
              max=cnodes;
          }
          clevel++;
          cnodes=1;
      }
    

       count<<cur.value<<level<<endl;
       if(cur.left!=null)              //有左孩子
       {
          levelMap.put(cur.left,level+1);
          queue.add(cur.left);
       }
       if(cur.right!=null)             //有右孩子
       {
          levelMap.put(cur.right,level+1);
          queue.add(cur.right);
       }
     }
    cout<<clevel<<cnodes<<endl;
    max= Math.max(max,cnodes);
    return max;

}

二叉树的递归套路（经典）

2.搜索二叉树：

左树节点小，右树都大。中序遍历：左中右，依次递增，那么就是搜索二叉树。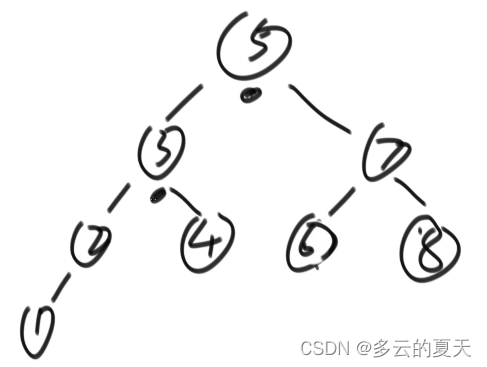

满足条件：
1.左子树整体是搜索二叉树。
2.右子树整体是搜索二叉树。
3.左树上的最大值小于head。
4.右树上的最小值大于head。

class Node
{
   public:
     int value;
     Node left;
     Node right;
    Node(int data)
   { 
     int value=data;
   }
}
//左小，右大
class Info{
   public:
   bool isBST;//是否是搜索二叉树
   int min;  //最小值
   int max;  //最大值
}

以x为head 返回3个信息

Info process(Node x)
{
   if(x==null)
{
}

//1.遍历左右两颗树
Info  leftData= process(x.left);
Info  rightData=process(y.left);

//2.更新左树和右树的最大最小值
int min=x.value;
int max=x.value;
if(leftData!=null){
    min=Math.min(min,leftData.min);
    max=Math.max(max,leftData.max);
}
if(rightData!=null){
    min=Math.min(min,rightData.min);
    max=Math.max(max,rightData.max);
  }


//3.左右两边是否是搜索二叉树呢
bool isBST =false;
//左树是搜索二叉树 左树最大值小于我
//右树是搜索二叉树 右树最小值大于我
if((leftData!=null ?(leftData.isBST && leftData.max<x.value):true)
   &&(rightData!=null ?(rightData.isBST && rightData.min>x.value):true))
{
   isBST =true;
}
}


bool isBSTTest(Node x)
{
  Info info=process(head);
  return info.isBST;
}

3.满二叉树：

判断条件：n=2^h-1

class Node
{
   public:
     int value;
     Node left;
     Node right;
    Node(int data)
    { 
      int value=data;
    }
};
//个数和高度
class Info{
   public:
   int nodes;   //个数
   int height;  //高度
   Info(int n,int h)
   {
       nodes=n;
       height=h;
   }

};

以x为head 返回3个信息
Info process(Node x)
{
   if(x==null)
   {
     return new Info(0,0);
   }
   //遍历左右两颗树
    Info  leftData= process(x.left);
    Info  rightData=process(y.left);
    int nodes;
    int height;
    int nodes=leftInfo.nodes+rightInfo.nodes+1;
    int height=Math.max(leftInfo.height,rightInfo.height)+1;
    return new Info(nodes,height);
};


bool isFull(Node head)
{
  Info info=process(head);
  int N =info.nodes;
  int h=info.height;
 //N=2^H-1
 return  N==(1<<H)-1;
}

4.平衡二叉树

左树跟右树的高度差不超过1

class Node
{
   public:
     int value;
     Node left;
     Node right;
    Node(int data)
    { 
      int value=data;
    }
};
//个数和高度
class Info{
   public:
   bool isBalanced;
   int height;  
   Info(bool is,int h)
   {
       isBalanced=is
       height=h;
   }

};

以x为head 返回3个信息
Info process(Node x)
{
   if(x==null)//空树
   {x
     return new Info(true,0);
   }
   //遍历左右两颗树
    Info  leftInfo= process(x.left);
    Info  rightInfo=process(x.right);
    bool isBalanced;
    int height;
    height=Math.max(leftInfo.height,rightInfo.height)+1;     

    //左树平
    //右树平
    //高度差值绝对值<2
    bool isBalanced=leftInfo.isBalanced && rightInfo.isBalanced &&
                    Math.abs(leftInfo.height-rightInfo.height)<2;
    return new Info(isBalanced,height);
};


bool isBalanced(Node head)
{
  Info info=process(head);
  return info.isBalanced;
}