欢迎关注我的CSDN:https://spike.blog.csdn.net/
本文地址:https://blog.csdn.net/caroline_wendy/article/details/130945234
Decaying Epsilon Greedy 算法是一种强化学习中的探索策略,可以平衡开发和探索之间的矛盾。基本思想是,以一个递减的概率 epsilon 随机选择一个动作,以 1-epsilon 的概率选择当前最优的动作。随着学习的进行,epsilon 逐渐减小,从而增加利用已知信息的机会,减少随机探索的次数。这种算法可以保证每个动作都有一定的概率被访问到,同时也可以收敛到最优策略。
1. 强化学习
强化学习(Reinforcement Learning):强化学习是机器通过与环境交互来实现目标的一种计算方法。
关注于:序列决策制定(Sequential Decision Making)
强化学习使用智能体或代理(Agent)表示做决策的机器,Agent包括3个要素,即感知(State)、决策(Action)、奖励(Return)。
类似于随机过程:
下一刻的状态
∼
P
(
⋅
∣
当前状态,智能体动作
)
下一刻的状态 \sim P(·|当前状态,智能体动作)
下一刻的状态∼P(⋅∣当前状态,智能体动作)
在交过过程中,每一轮获得的奖励信号可以进行累加,形成智能体的整体回报(Return),而回报的期望,就是价值(Value)。
强化学习的数据分布,即占用度量(Occupancy Measure)。
有监督学习,数据分布不变,优化模型:
最优模型
=
a
r
g
m
i
n
模型
E
(
特征、标签
)
∼
数据分布
[
损失函数
(
标签,模型
(
特征
)
)
]
最优模型 = \underset{模型}{arg \ min} \ E_{(特征、标签)\sim数据分布}[损失函数(标签,模型(特征))]
最优模型=模型arg min E(特征、标签)∼数据分布[损失函数(标签,模型(特征))]
强化学习,数据分布变化,优化策略:
最优策略
=
a
r
g
m
a
x
策略
E
(
状态、动作
)
∼
策略的占用度量
[
奖励函数
(
状态、动作
)
]
最优策略 = \underset{策略}{arg \ max} \ E_{(状态、动作) \sim 策略的占用度量}[奖励函数(状态、动作)]
最优策略=策略arg max E(状态、动作)∼策略的占用度量[奖励函数(状态、动作)]
2. 多臂老虎机问题
多臂老虎机(Multi-Armed Bandit)问题,只有动作和奖励,没有状态,主要关注于探索(Exploration)和利用(Exploitation),即探索拉杆的获奖概率,根据经验选择获奖最多的拉杆(根据期望),设计策略,平衡探索和利用的次数,使得累积奖励最大化。
懊悔值(Regret)类似于损失值,最大化累积奖励,等价于最小化累积懊悔。
期望更新公式,
r
k
r_{k}
rk 是第 k 次的奖励值,增量更新的时间复杂度O(1):
Q
k
=
Q
k
−
1
+
1
k
[
r
k
−
Q
k
−
1
]
Q_{k} = Q_{k-1} + \frac{1}{k}[r_{k} - Q_{k-1}]
Qk=Qk−1+k1[rk−Qk−1]
3. Decaying Epsilon Greedy 算法
ϵ
-
G
r
e
e
d
y
\epsilon \ \text{-} \ Greedy
ϵ - Greedy 算法,在完全贪婪算法的基础上,增加噪声
ϵ
\epsilon
ϵ,每次以概率
1
−
ϵ
1-\epsilon
1−ϵ 选择以往经验中期望奖励估值最大的拉杆(利用),以概率
ϵ
\epsilon
ϵ 随机选择一根拉杆(探索),公式如下:
a
i
=
{
a
r
g
m
a
x
a
∈
A
Q
(
a
)
,采样概率
1
−
ϵ
从
A
中随机选择,采样概率
ϵ
a_{i} = \begin{cases} arg \ \underset{a \in A}{max} \ Q(a),采样概率 \ 1-\epsilon \\ 从A中随机选择,采样概率 \ \epsilon \\ \end{cases}
ai={arg a∈Amax Q(a),采样概率 1−ϵ从A中随机选择,采样概率 ϵ
ϵ
-
G
r
e
e
d
y
\epsilon \ \text{-} \ Greedy
ϵ - Greedy 算法,累积懊悔是线性增长的。优化的
D
e
c
a
y
i
n
g
ϵ
-
G
r
e
e
d
y
Decaying \ \epsilon \ \text{-} \ Greedy
Decaying ϵ - Greedy 算法,
ϵ
\epsilon
ϵ 值随时间
t
t
t 衰减,反比例衰减,即
ϵ
=
1
t
\epsilon = \frac{1}{t}
ϵ=t1 累计懊悔是次线性(sublinear)增长的,优于
ϵ
-
G
r
e
e
d
y
\epsilon \ \text{-} \ Greedy
ϵ - Greedy 算法。
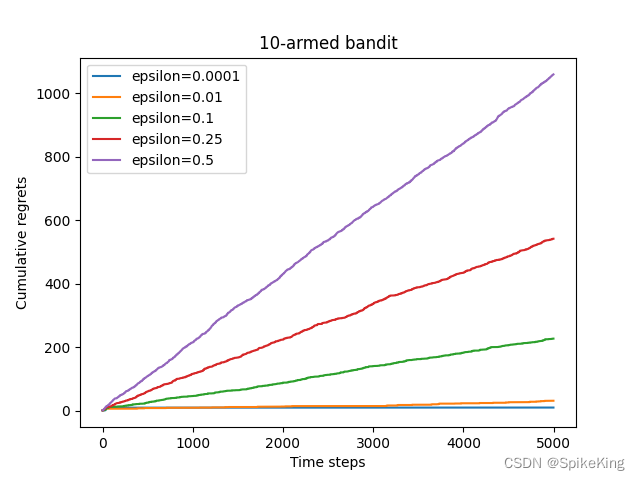
ϵ - G r e e d y \epsilon \ \text{-} \ Greedy ϵ - Greedy 算法:
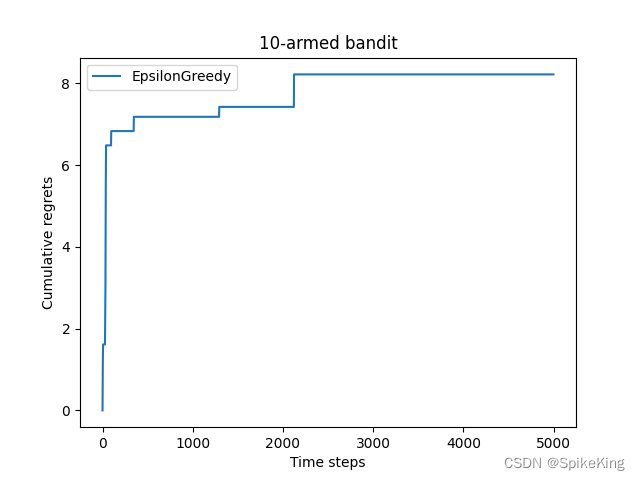
D e c a y ϵ - G r e e d y Decay \ \epsilon \ \text{-} \ Greedy Decay ϵ - Greedy 算法:
源码如下:
class BernoulliBandit(object):
"""
经典的 Bernoulli 多臂老虎机
"""
def __init__(self, K, seed=42):
np.random.seed(seed)
self.probs = np.random.uniform(size=K)
self.best_idx = np.argmax(self.probs)
self.best_prob = self.probs[self.best_idx]
self.K = K
print(f"随机生成一个 {K} 臂的伯努利老虎机")
print(f"老虎机获奖概率: {[round(i, 4) for i in self.probs]}")
print(f"获奖概率最大的拉杆是 {self.best_idx} 号,相应的获奖概率是 {round(self.best_prob, 4)}")
def step(self, k):
if np.random.rand() < self.probs[k]:
return 1
else:
return 0
class Solver(object):
"""
MAB 求解的基类
"""
def __init__(self, bandit):
self.bandit = bandit
self.counts = np.zeros(self.bandit.K) # 记录动作选择数量
self.regret = 0. # 累计懊悔值
self.actions = [] # 记录每一步的动作
self.regrets = [] # 记录每一步的懊悔
def update_regret(self, k):
"""
更新懊悔值
"""
self.regret += self.bandit.best_prob - self.bandit.probs[k] # 概率懊悔值
self.regrets.append(self.regret) # 记录概率懊悔值
def run_one_step(self):
"""
返回拉动哪一根拉杆
1. 根据策略选择动作
2. 根据动作获得奖励
3. 更新期望奖励估值
"""
raise NotImplementedError
def run(self, num_steps): # 执行
for _ in range(num_steps):
k = self.run_one_step() # 动作是k
self.counts[k] += 1 # 更新选择次数
self.actions.append(k)
self.update_regret(k) # 更新懊悔值
class EpsilonGreedy(Solver):
"""
Epsilon Greedy 算法
"""
def __init__(self, bandit, epsilon=0.01, init_prob=1.0):
super(EpsilonGreedy, self).__init__(bandit)
self.epsilon = epsilon
# 初始化全部拉杆的期望,后续逐渐更新
self.estimates = np.array([init_prob] * self.bandit.K)
def run_one_step(self):
if np.random.random() < self.epsilon:
k = np.random.randint(0, self.bandit.K) # 随机选择一个拉杆
else:
k = np.argmax(self.estimates) # 选择最大期望的拉杆
r = self.bandit.step(k)
# 更新期望,先run,再更新count,所以count+1,更新期望
self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
return k
class DecayingEpsilonGreedy(Solver):
"""
随着时间衰减的 Epsilon-Greedy 算法
"""
def __init__(self, bandit, init_prob=1.0):
super(DecayingEpsilonGreedy, self).__init__(bandit)
self.estimates = np.array([init_prob] * self.bandit.K)
self.total_count = 0
def run_one_step(self):
self.total_count += 1
epsilon = 1 / self.total_count
if np.random.random() < epsilon:
k = np.random.randint(0, self.bandit.K)
else:
k = np.argmax(self.estimates)
r = self.bandit.step(k)
self.estimates[k] += 1 / (self.counts[k] + 1) * (r - self.estimates[k])
return k