文章目录
- 第二章——算法分析
- 2.1 算法评价的量化理论
- 2.1.1 函数渐进增长
- 四种渐进增长定义
- 运算法则
- 两个函数相对增长率判断
- 2.1.2 算法分析的计算机模型
- 2.1.3 要分析的目标
- 最坏情况
- 2.1.4 一般法则
- for循环
- 嵌套for循环
- 顺序语句
- 分支语句
- 二分
- 函数调用
- 2.2 计算方法
- 2.2.1 循环主体中的变量参与循环条件的判断
- 模拟法优化递归
- 斐波那契数列
- 阶乘计算
- 运算时间中的对数
- 折半查找
- 欧几里得算法——求最大公约数
- 快速幂
- 2.2.2 循环主体中的变量与循环条件无关
- 暴力法分析
- 分治法
- 策略
- *推导*
- 2.2.3 常见算法时间复杂度
- 2.3 最大子序列和问题求解
- 2.3.1 遍历所有子串,对子串的子序列依次求和
- 2.3.2 记录中间累加量
- 2.3.3 分治法
- 2.3.4 最简
- 2.4 空间复杂度
- 原地工作
- 2.5 习题
- 2.5.7 随机数序列生成算法
- 2.5.9 多项式计算
- 2.5.13 判断一个正整数是否为素数
算法是为求解一个问题需要遵循的、被清楚指定的简单指令的集合
第二章——算法分析
- 如何估计一个程序的运行时间
- 如何降低程序运行时间
- 一些经典案例
2.1 算法评价的量化理论
估计算法所需的资源消耗分析一般来说是理论问题——需要一套数学基础提供理论支撑
将核心操作的次数与输入规模关联
2.1.1 函数渐进增长
算法分析是衡量对象:某个算法的时间复杂度随输入规模增大的变化率
需要约定一个通用基准,才能通过对比,直观的判断变化率的大小
- 上界
- 下界
- 等价
四种渐进增长定义
函数渐进增长是要在函数间建立一种相对的级别——相对增长率
给定两个函数 f ( N ) f(N) f(N) 和 g ( N ) g(N) g(N) ,如果存在一个整数 N 0 N_0 N0 使得对于所有 N > N 0 N >N_0 N>N0 , f ( N ) f(N) f(N) 总是比 g ( N ) g(N) g(N) 大,那么称 f ( N ) f(N) f(N) 的渐进增长快于 g ( N ) g(N) g(N)
-
上界:如果存在正常数 c c c 和 N 0 N_0 N0 使得 当 N ≥ N 0 N\ge N_0 N≥N0 时, T ( N ) ≤ c f ( N ) T(N)\le cf(N) T(N)≤cf(N) ,则记为 T ( N ) = O ( f ( N ) ) T(N)=O(f(N)) T(N)=O(f(N))

- T ( N ) T(N) T(N) 的增长率小于等于( ≤ \le ≤) f ( N ) f(N) f(N) —— f ( N ) f(N) f(N) 是 T ( N ) T(N) T(N) 的一个上界
-
如果存在正常数 c c c 和 N 0 N_0 N0 使得当 N ≥ N 0 N\ge N_0 N≥N0 时, T ( N ) ≥ c g ( N ) T(N)\ge cg(N) T(N)≥cg(N) ,则记为 T ( N ) = Ω ( g ( N ) ) T(N)=\Omega(g(N)) T(N)=Ω(g(N))

- T ( N ) T(N) T(N) 的增长率大于等于( ≥ \ge ≥) g ( N ) g(N) g(N) 的增长率—— g ( N ) g(N) g(N) 是 T ( N ) T(N) T(N) 的一个下界
-
如果存在正常数 c 1 c_1 c1 、 c 2 c_2 c2 、 N 0 N_0 N0 、 N 1 N_1 N1 ,使得当 N ≥ N 0 N\ge N_0 N≥N0 时,有 T ( N ) ≥ c 0 h ( N 0 ) T(N)\ge c_0h(N_0) T(N)≥c0h(N0) 且当 N ≥ N 1 N\ge N_1 N≥N1 时,有 T ( N ) ≥ c 1 h ( N 1 ) T(N)\ge c_1h(N_1) T(N)≥c1h(N1) ,则记为 T ( N ) = Θ ( h ( N ) ) T(N)=\Theta(h(N)) T(N)=Θ(h(N))
- T ( N ) = Θ ( h ( N ) ) T(N)=\Theta(h(N)) T(N)=Θ(h(N)) 当且仅当 T ( N ) = O ( h ( N ) ) T(N)=O(h(N)) T(N)=O(h(N)) 且 T ( N ) = Ω ( h ( N ) ) T(N)=\Omega(h(N)) T(N)=Ω(h(N))
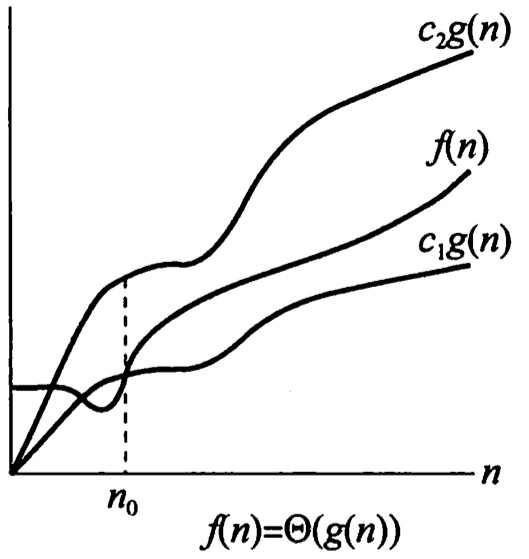
- T ( N ) T(N) T(N) 的增长率等于( = = =) h ( N ) h(N) h(N) 的增长率
-
如果 T ( n ) = O ( p ( N ) ) T(n)=O(p(N)) T(n)=O(p(N)) 且 T ( N ) ≠ Θ ( N ) T(N)\neq \Theta(N) T(N)=Θ(N) ,则 T ( N ) = o ( p ( N ) ) T(N)=o(p(N)) T(N)=o(p(N))
- T ( N ) T(N) T(N) 的增长率大于 (>) p ( N ) p(N) p(N) 的增长率
运算法则
-
如果 T 1 ( N ) = O ( f ( N ) ) T_1(N)=O(f(N)) T1(N)=O(f(N)) 且 T 2 ( N ) = Ω ( g ( N ) ) T_2(N)=\Omega(g(N)) T2(N)=Ω(g(N)) ,则
- 并列结构: T 1 ( N ) + T 2 ( N ) = m a x ( O ( f ( N ) ) , O ( g ( N ) ) ) T_1(N)+T_2(N)=max(O(f(N)),O(g(N))) T1(N)+T2(N)=max(O(f(N)),O(g(N)))
- 嵌套结构: T 1 ( N ) ∗ T 2 ( N ) = O ( f ( N ) ∗ g ( N ) ) T_1(N)*T_2(N)=O(f(N)*g(N)) T1(N)∗T2(N)=O(f(N)∗g(N))
-
如果 T ( N ) T(N) T(N) 是一个 k k k 次多项式,则 T ( N ) = Θ ( N k ) T(N)=\Theta(N^k) T(N)=Θ(Nk)
-
对任意常数 k k k , l o g k ( N ) = O ( N ) log^k(N)=O(N) logk(N)=O(N) ——对数增长很缓慢
-
几种典型的增长率排序

- O ( 1 ) < O ( l o g n ) < O ( n ) < O ( n l o g n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 n ) < O ( n ! ) < O ( n n ) O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n) O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
-
在渐进增长函数中省略所有的常数,系数
修改后的次数中,只保留高阶项
两个函数相对增长率判断
洛必达
通过 lim n → ∞ f ( N ) g ( N ) \lim_{n\rightarrow\infty}\limits \frac{f(N)}{g(N)} n→∞limg(N)f(N) 确定两个函数 f ( N ) f(N) f(N) 和 g ( N ) g(N) g(N) 的相对增长率
- 0 0 0 : f ( N ) = o ( g ( N ) ) f(N)=o(g(N)) f(N)=o(g(N))
- c ≠ 0 c\neq 0 c=0 : f ( N ) = Θ ( N ) f(N)=\Theta(N) f(N)=Θ(N)
- ∞ \infty ∞ : g ( N ) = o ( f ( N ) ) g(N)=o(f(N)) g(N)=o(f(N))
2.1.2 算法分析的计算机模型
有一个简单的指令系统:加法、乘法、比较和赋值
模型机做任何一个简单的工作,都花费一个时间单元
模型机有无限内存
2.1.3 要分析的目标
算法分析的最重要的资源一般来说是运行时间
事前分析:
- 算法采用的策略和方案
- 编译产生代码质量
- 问题的输入规模
- 机器执行指令的速度
编译器和计算机执行速度超过了理论分析范畴,所以在算法分析中,重点考虑 算法采用的策略 以及 输入规模
输入的大小是主要的考虑方面, T a v g ( N ) T_{avg}(N) Tavg(N) 和 T w o r s t ( N ) T_{worst}(N) Tworst(N) 分别表示算法花费的平均运行时间和最坏情况下运行时间
而算法的平均情况的界计算起来通常很困难,所以一般情况算法分析的是 最坏情况下的运行时间
所以实际上计算的是 大O运行时间 ,该分析结果为程序在一定的时间范围内能够终止运行提供了保障。程序可能提前结束,但绝不可能拖后
∑ i = 1 N i 3 \sum_{i=1}\limits^{N}i^3 i=1∑Ni3
# 累加
int main(){
int sum = 0;//执行一次
int n = 100;//执行一次
for(int i = 0; i < n;++i){
//赋值1次,比较语句执行n+1次,自增执行n+1次
sum += i*i*i;
//加法执行n次,乘法执行2n次,赋值n次
}
printf("sum=%d",sum);//执行一次
}
# 执行 6n+4 次
# 大O记法 O(n)
最坏情况
直接查找
int search(int num){
int arr[] = [11,10,8,9,7,22,23,0];
for(int i = 0;i < arr.length;++i){
if(num == arr[i])
return i;
}
return -1;
}
最好情况:
- 查找的第一个数字就是期望数字—— O ( 1 ) O(1) O(1)
最坏情况:
- 查找的最后一个数字,才是期望数字—— O ( n ) O(n) O(n)
平均情况:
- 任何数字查找的平均代价为 —— O ( n ) O(n) O(n)
2.1.4 一般法则
for循环
for(int i=0;i < N;++i){}
T ( N ) = O ( T ( { } ) × N ) T(N)=O(T(\{\})\times N) T(N)=O(T({})×N)
嵌套for循环
for(int i=0;i < N1;++i){
for(int j=0;j < N2;++j){
...
}
}
T ( N ) = O ( T ( { } ) × N 1 × N 2 × . . . ) T(N)=O(T(\{\})\times N1\times N2\times...) T(N)=O(T({})×N1×N2×...)
顺序语句
将各个语句的运行时间求和——最大值就是整体的运行时间
for(int i = 0;i < N;++i){
A[i] = 0;
}
for(int i = 0;i < N;++i){
for(int j = 0;j < N;++j){
A[i] += A[j]+i+j;
}
}
T ( N ) = m a x { O ( N ) , O ( N 2 ) } = O ( N 2 ) T(N)=max\{O(N),O(N^2)\}=O(N^2) T(N)=max{O(N),O(N2)}=O(N2)
分支语句
if(condition) S1;
else S2;
T ( N ) = O ( T { c o n d i t i o n } + m a x { T ( S 1 ) , T ( S 2 ) } ) T(N)=O(T\{condition\}+max\{T(S1),T(S2)\}) T(N)=O(T{condition}+max{T(S1),T(S2)})
二分
对数阶,由于输入规模n的增大,不管底数多少,增长率都相同,所以忽略底数
int i=1,n=100;
while(i < n){
i = i*2;
}
循环次数: x = l o g 2 n x = log_2n x=log2n
- 时间复杂度: O ( l o g n ) O(logn) O(logn)
函数调用
先分析被调用的函数,再分析回调函数
void main(){
int n = 100;
for(int i = 0;i < n;++i){
show(i); // O(n)
}
}
void show(int i){
printf("%d",i);
}
void main(){
int n = 100;
for(int i = 0;i < n;++i){
show(i); //O(n^2)
}
}
void show(int i){
for(int j = 0;j < i;++j){
printf("%d",i);
}
}
2.2 计算方法
2.2.1 循环主体中的变量参与循环条件的判断
找出主体语句中与 T ( n ) T(n) T(n) 成正比的循环变量,将之代入条件运算
int i = 1;
while(i <= n){
i = i*2;
}
- 执行次数 t t t ,有 2 t ≤ n 2^t \leq n 2t≤n ,得 T ( n ) = O ( l o g 2 n ) T(n) = O(log_2n) T(n)=O(log2n)
int y = 5;
while((y+1)*(y+1)<=n){
y = y+1;
}
- 当 ( y + 1 ) 2 = ⌊ n ⌋ (y+1)^2=\lfloor\sqrt{n}\rfloor (y+1)2=⌊n⌋ 时,得到执行次数 t = ⌊ n ⌋ − 6 t = \lfloor\sqrt{n}\rfloor-6 t=⌊n⌋−6 ,即 T(n) = O( n \sqrt{n} n)
模拟法优化递归
斐波那契数列与阶乘的计算
- 输入
N
N
N 作为计算的终止条件
- f u n ( N ) fun(N) fun(N) 的计算依赖于 f u n ( N − 1 ) . . . f u n ( N − k ) fun(N-1)...fun(N-k) fun(N−1)...fun(N−k)
- 不适用分治
斐波那契数列
{ F ( 0 ) = 0 , F ( 1 ) = 1 F ( N ) = F ( N − 1 ) + F ( N − 2 ) , N ≥ 2 \begin{aligned} \left\{ \begin{aligned} &F(0)=0,F(1)=1\\ &F(N)=F(N-1)+F(N-2),N\ge 2 \end{aligned} \right. \end{aligned} {F(0)=0,F(1)=1F(N)=F(N−1)+F(N−2),N≥2
long int Fib(int N){
if(N <= 1)
return N;
else
return Fib(N-1)+Fib(N-2);
}
- 如果 N = 0 N=0 N=0 或 N = 1 N=1 N=1 ,运行时间是常数值—— O ( 1 ) O(1) O(1)
- 如果
N
≥
2
N\ge 2
N≥2 ,则
T
(
N
)
=
T
(
N
−
1
)
+
T
(
N
−
2
)
+
2
T(N)=T(N-1)+T(N-2)+2
T(N)=T(N−1)+T(N−2)+2
F i b ( N ) = F i b ( N − 1 ) + F i b ( N − 2 ) Fib(N)=Fib(N-1)+Fib(N-2) Fib(N)=Fib(N−1)+Fib(N−2) ,由归纳法可知 T ( N ) ≥ F i b ( N ) T(N)\ge Fib(N) T(N)≥Fib(N)
由归纳法可以证明: F i b ( N ) < ( 5 3 ) N Fib(N)<(\frac{5}{3})^N Fib(N)<(35)N ,同样可得 ( 3 2 ) N ≤ F i b ( N ) , ( N > 4 ) (\frac{3}{2})^N\le Fib(N),(N>4) (23)N≤Fib(N),(N>4)
可见, ( 3 2 ) N ≤ F i b ( N ) ≤ T ( N ) (\frac{3}{2})^N\le Fib(N)\le T(N) (23)N≤Fib(N)≤T(N)
故通过递归程序计算斐波那契数列,时间复杂度为 O ( 2 N ) O(2^N) O(2N)
之所以是指数时间,是因为存在大量重复计算——计算任何事物不要超过一次
优化斐波那契数列求解
//记忆搜索
long int memo[MAX_N+1];
long int Fib1(int N){
if(N <= 1)
return N;
//此时有未计算和已经计算好并存储到数据中的两种情况
if(memo[N] != 0)//等于0的情况在Fib数列中只有第一项
return memo[N]
else{
return memo[N]=Fib1(N-1)+Fib(N-2);
}
}
对于规模较小的输入可以得到输出,单对于大规模的输入,仍相当于指数阶
long int Fib2(long int N){
if(N <= 1)
return N;
long int first = 0,second = 1;
for(int i = 2;i <= N;==i){
third = first + second;
first = second;
second = third;
}
return third;
}
- 时间复杂度为 O ( N ) O(N) O(N)
阶乘计算
n ! = 1 × 2 × 3 × ⋯ n!=1\times 2\times 3\times\cdots n!=1×2×3×⋯
//计算阶乘 ,递归定义
long long fac0(int n){
//计算到25
if(n <= 1)
return 1;
return n*fac0(n-1);
}
优化算法相当于模拟乘法的手算过程,用数组元素代表数位。将计算结果按位依次存储到数组中,然后逆序输出
例如:求 5 ! 5! 5!
i = 2
a[1]=1
tmp=a[1]*2+0=2;
a[1]=2;
===================
i=3
a[1]=2
tmp=a[1]*3+0=6;
a[1]=6;
===================
i=4
a[1]=6
tmp=a[1]*4+0=24;
a[1]=24%10=4;
carry=24/10=2;
length++;
a[2]=0
tmp=a[2]*4+2=2;
a[2]=2;
===================
i=5
a[1]=4
a[2]=2
tmp=a[1]*5=20;
a[1]=20%10=0;
carry=20/10=2;
length = 2;
tmp=a[2]*5+carry=12;
a[2]=12%10=2;
carry=20/10=1;
length = 3;
tmp=a[3]*5+carry=1;
a[2]=1;
=====================
print(a[3],a[2],a[1]);120
void print_fac(int n){
if(n <= 1)
cout << "1" << endl;
else{
int a[500000] = {0,1};//a[0]用不上,将其他初始化为1
int carry,length = 1,tmp;
//carry:若有进位,则存储;若无,0
//length:若有进位,则继续计算;若无默认计算一次
//tmp:存储当前位的计算结果
for(int i = 2;i <= n;++i){
carry = 0;
for(int j = 1;j <= length;++j){
tmp = a[j] * i + carry;
a[j] = tmp % 10;
carry = tmp / 10;
if(j == length && carry)
length++;
}
}
for(int i = length;i >= 1;--i)
cout << a[i];
}
}
int main(){
int n;
cin >> n;
print_fac(n);
return 0;
}
- 时间复杂度为 O ( N ) O(N) O(N)
通过运行结果,可以看到按定义(即递归),最多只能算到25
而改进之后的算法,可以看到算到70000都没有崩,对于一般的竞赛来说已经足够了

运算时间中的对数
- 如果一个算法用常数时间 ( O ( 1 ) ) \left(O(1)\right) (O(1)) 将问题的规模削减为原来的一部分(一般为一半),那么该算法就是 O ( l o g N ) O(logN) O(logN)
- 如果用常数时间把问题规模削减为一个常数,那么这种算法就是 O ( N ) O(N) O(N)
折半查找
更定一个目标元素
X和 有序 整数序列 A 0 A_0 A0 、 A 1 A_1 A1、…、 A N − 1 A_{N-1} AN−1 ,求得使 A i = X A_i=X Ai=X 的下标 i i i ;如果X不存在与序列,则返回 i = − 1 i=-1 i=−1
int BinarySearch(const ElementType A[],ElementType X,int N){
int Low,Mid,High;
Low = 0,High = N-1;
while(Low <= High){
Mid = (Low+High)/2;
if(A[Mid] < X){
Low = Mid + 1;
}else{
if(A[Mid] > X){
High = Mid-1;
else
return Mid; //Found
}
}
return NotFound; //NotFound is defined as -1
}
在 while 循环体中,时间复杂度为
O
(
1
)
O(1)
O(1) ——
T
(
N
)
=
O
(
1
)
T(N)=O(1)
T(N)=O(1)
循环次数最多为 ⌈ l o g ( N − 1 ) ⌉ + 2 \lceil log(N-1)\rceil+2 ⌈log(N−1)⌉+2
- 若 h i g h − l o w = 128 high-low=128 high−low=128 ,迭代过程中, h i g h − l o w high-low high−low 最大值是 64,32,16,8,4,2,1,0,-1
故二分查找时间复杂度为 T ( N ) = O ( T ( { } ) × ( ⌈ l o g ( N − 1 ) ⌉ + 2 ) ) = O ( l o g N ) T(N)=O(T(\{\})\times (\lceil log(N-1)\rceil+2))=O(logN) T(N)=O(T({})×(⌈log(N−1)⌉+2))=O(logN)
适用于静态数据的查找——不允许数据的插入和删除
欧几里得算法——求最大公约数
定理:如果 M ≥ N ≥ 1 M\ge N\ge 1 M≥N≥1 ,则 KaTeX parse error: Undefined control sequence: \mbox at position 3: M \̲m̲b̲o̲x̲{ mod N} < \fra…
- 如果 N ≤ M 2 N\le\frac{M}{2} N≤2M ,则由于余数小于 N N N ,有 KaTeX parse error: Undefined control sequence: \mbox at position 38: …}\Rightarrow M \̲m̲b̲o̲x̲{ mod N} < \fra…
- 如果 N > M 2 N>\frac{M}{2} N>2M ,则 M % N = M − N < M 2 M\%N=M-N<\frac{M}{2} M%N=M−N<2M
unsigned int Gcd(unsigned int M,unsigned int N){
if(N>M)
swap(M,N);
unSigned int Rem;
while(N > 0){
Rem = M % N;
M = N;
N = Rem;
}
return M;
}
在循环体中,时间复杂度为 T ( { } ) = O ( 1 ) T(\{\})=O(1) T({})=O(1)
接下来重点是计算迭代次数
可以根据定理,粗略的认为:每次迭代可以在常数时间内使 M M M 减少一半,故迭代次数为 O ( l o g N ) O(logN) O(logN)
令
R
e
m
0
=
M
,
R
e
m
1
=
N
Rem_0=M,Rem_1=N
Rem0=M,Rem1=N
R
e
m
2
=
R
e
m
0
%
R
e
m
1
R
e
m
3
=
R
e
m
1
%
R
e
m
2
⋯
R
e
m
n
+
1
=
R
e
m
n
−
1
%
R
e
m
n
}
⇒
R
e
m
k
+
1
+
R
e
m
k
+
2
≤
R
e
m
k
\begin{equation} \left. \begin{aligned} Rem_2=Rem_0\% Rem_1\\ Rem_3=Rem_1\% Rem_2\\ \cdots\\ Rem_{n+1}=Rem_{n-1}\% Rem_{n} \end{aligned} \right\}\Rightarrow Rem_{k+1}+Rem_{k+2}\le Rem_k \end{equation}
Rem2=Rem0%Rem1Rem3=Rem1%Rem2⋯Remn+1=Remn−1%Remn⎭
⎬
⎫⇒Remk+1+Remk+2≤Remk
迭代
n
n
n 次后,
R
e
m
n
+
1
=
0
Rem_{n+1}=0
Remn+1=0 ,
R
e
m
n
≥
0
Rem_{n}\ge 0
Remn≥0 即为最大公约数
观察斐波那契数列
{
F
b
0
=
0
F
b
1
=
1
F
b
k
=
F
b
k
−
1
+
F
b
k
−
2
\begin{aligned} \left\{ \begin{aligned} &Fb_0=0\\ &Fb_1=1\\ &Fb_{k}=Fb_{k-1}+Fb_{k-2} \end{aligned} \right. \end{aligned}
⎩
⎨
⎧Fb0=0Fb1=1Fbk=Fbk−1+Fbk−2
可知:
F
b
0
=
0
≤
R
e
m
n
F
b
1
=
1
≤
R
e
m
n
−
1
\begin{aligned} &Fb_0=0\le Rem_n\\ &Fb_1=1\le Rem_{n-1}\\ \end{aligned}
Fb0=0≤RemnFb1=1≤Remn−1
不妨假设:
F
b
k
≤
R
e
m
n
−
k
Fb_{k}\le Rem_{n-k}
Fbk≤Remn−k ,由归纳法
n
=
0
和
n
=
1
成立
假设
F
b
k
≤
F
b
n
−
k
F
b
k
+
1
=
F
b
k
+
F
b
k
−
1
≤
R
e
m
n
−
k
+
R
e
m
n
−
k
+
1
≤
R
e
m
n
−
k
−
1
k
=
k
+
1
时,有
F
b
k
+
1
≤
R
e
m
n
−
k
−
1
成立
∴
F
b
k
≤
R
e
m
n
−
k
\begin{aligned} &n=0和n=1成立\\ &假设Fb_{k}\le Fb_{n-k}\\ &Fb_{k+1}=Fb_{k}+Fb_{k-1}\le Rem_{n-k}+Rem_{n-k+1}\le Rem_{n-k-1}\\ &k=k+1时,有 Fb_{k+1}\le Rem_{n-k-1}成立\\ &\therefore Fb_{k}\le Rem_{n-k} \end{aligned}
n=0和n=1成立假设Fbk≤Fbn−kFbk+1=Fbk+Fbk−1≤Remn−k+Remn−k+1≤Remn−k−1k=k+1时,有Fbk+1≤Remn−k−1成立∴Fbk≤Remn−k
由于
R
e
m
1
=
N
≥
F
b
n
−
1
=
1
5
[
(
1
+
5
2
)
n
−
1
−
(
1
−
5
2
)
n
−
1
]
⇒
n
=
O
(
l
o
g
N
)
Rem_1=N\ge Fb_{n-1}=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n-1}-\left(\frac{1-\sqrt{5}}{2}\right)^{n-1}\right]\Rightarrow n=O(logN)
Rem1=N≥Fbn−1=51[(21+5)n−1−(21−5)n−1]⇒n=O(logN)
- 故其时间复杂度为 T ( N ) = O ( T { } × l o g ( N ) ) = O ( l o g N ) T(N)=O(T\{\}\times log(N))=O(logN) T(N)=O(T{}×log(N))=O(logN)
快速幂
计算 x n x^n xn
long int Pow(long int x,unsigned int n){
long int res = 1;
for(int i = 0;i < n;++i){
res *= x;
}
return res;
}
long int Pow(long int x,unsigned int n){
if(n == 1)
return x;
return x*Pow(x,n-1);
}
- 时间复杂度为 O ( N ) O(N) O(N)
long int Pow(long int X,unsigned int N){
if(N == 0)
return 1;
if(N == 1)
return X;
if(isEven(N))
return Pow(X*X,N/2);
else
return Pow(X*X,N/2) * X;
}
- 若 N N N 是偶数,则 X N = X N 2 ⋅ X N 2 X^N=X^{\frac{N}{2}}\cdot X^{\frac{N}{2}} XN=X2N⋅X2N
- 若 N N N 是奇数,则 X N = X ⋅ X N − 1 2 ⋅ X N − 1 2 X^N=X\cdot X^{\frac{N-1}{2}}\cdot X^{\frac{N-1}{2}} XN=X⋅X2N−1⋅X2N−1
将问题对半分,每个子问题最多需要两次乘法
T { } = 2 T\{\}=2 T{}=2 ,函数调用次数为 l o g N logN logN,故时间复杂度 T { N } = O ( T { } × l o g N ) = O ( 2 l o g N ) = O ( l o g N ) T\{N\}=O(T\{\}\times logN)=O(2logN)=O(logN) T{N}=O(T{}×logN)=O(2logN)=O(logN)
快速幂非递归形式
原理:
-
计算 X X X 不大于 N N N 的二次幂序列 X , X 2 , X 4 , ⋯ , X 2 ⌊ l o g N ⌋ X,X^2,X^4,\cdots,X^{2^{\lfloor logN\rfloor}} X,X2,X4,⋯,X2⌊logN⌋
时间复杂度为 O ( l o g N ) O(logN) O(logN)
-
将 X X X 用二进制表示,将
1位对应的二次幂相乘就是 X X X 的 N N N 次幂通过取余求1的个数,最多计算 ⌊ l o g N ⌋ + 1 {\lfloor logN\rfloor}+1 ⌊logN⌋+1 次
通过 popcount,时间复杂度会更少
两个计算步骤是并列的,所以时间复杂度为 O ( l o g N ) O(logN) O(logN)
例:计算 X 62 X^{62} X62
-
计算并保存序列: X , X 2 , X 4 , X 8 , X 16 , X 32 X,X^2,X^4,X^8,X^{16},X^{32} X,X2,X4,X8,X16,X32
计算 ⌊ l o g 62 ⌋ = 5 \lfloor log62\rfloor=5 ⌊log62⌋=5 次
-
62 62 62 的二进制表示为
11 1110通过 ⌊ l o g 62 ⌋ = 5 \lfloor log62\rfloor=5 ⌊log62⌋=5 次计算得到1的个数
同时计算 X 62 = X 32 ⋅ X 16 ⋅ X 8 ⋅ X 4 ⋅ X 2 X^{62}=X^{32}\cdot X^{16}\cdot X^{8}\cdot X^{4}\cdot X^{2} X62=X32⋅X16⋅X8⋅X4⋅X2
进行5次乘法
int pow(int X,int n){
//X 底数
//n 幂次
int res = 1;
while (n != 0) {
if ((n & 1) == 1) {//如果满足条件,则相乘
res = res * X;
}
//无论如何,X都要不断倍增,n都要不断右移
X *= X;
n = n >> 1;
}
return res;
}
int pow(int X,int n){
//X 底数
//n 幂次
int res = 1;
int tmp = X;
while (n != 0) {
if ((n & 1) == 1) {//如果满足条件,则相乘
res = res * tmp;
}
tmp = tmp * tmp;
n = n >> 1;
}
return res;
}
快速幂时间复杂度为一个上界,实际执行次数不一定等于上界
例:分析计算 X 62 X^{62} X62 需要的乘法次数
按照快速幂的思想:
2
l
o
g
(
62
)
=
10
2log(62)=10
2log(62)=10
X
62
=
X
31
⋅
X
31
x
31
=
X
⋅
X
15
⋅
X
15
x
15
=
X
⋅
X
7
⋅
X
7
x
7
=
X
⋅
X
3
⋅
X
3
x
3
=
X
⋅
X
1
⋅
X
1
\begin{aligned} X^{62}=X^{31}\cdot X^{31}\\ x^{31}=X\cdot X^{15}\cdot X^{15}\\ x^{15}=X\cdot X^{7}\cdot X^{7}\\ x^{7}=X\cdot X^{3}\cdot X^{3}\\ x^{3}=X\cdot X^{1}\cdot X^{1} \end{aligned}
X62=X31⋅X31x31=X⋅X15⋅X15x15=X⋅X7⋅X7x7=X⋅X3⋅X3x3=X⋅X1⋅X1
需要9次乘法
也可以通过
X
2
=
X
⋅
X
X
4
=
X
2
⋅
X
2
X
8
=
X
4
⋅
X
4
X
10
=
X
8
⋅
X
2
X
20
=
X
10
⋅
X
10
X
40
=
X
20
⋅
X
20
X
60
=
X
40
⋅
X
20
X
62
=
X
60
⋅
X
2
X^2=X\cdot X\\ X^4=X^2\cdot X^2\\ X^8=X^4\cdot X^4\\ X^{10}=X^{8}\cdot X^2\\ X^{20}=X^{10}\cdot X^{10}\\ X^{40}=X^{20}\cdot X^{20}\\ X^{60}=X^{40}\cdot X^{20}\\ X^{62}=X^{60}\cdot X^{2}
X2=X⋅XX4=X2⋅X2X8=X4⋅X4X10=X8⋅X2X20=X10⋅X10X40=X20⋅X20X60=X40⋅X20X62=X60⋅X2
可见通过8次乘法也是能计算出
X
62
X^{62}
X62
2.2.2 循环主体中的变量与循环条件无关
采用 归纳法 或 累计循环次数
多层循环从内到外分析,忽略单步语句、条件判断语句,只关注主体语句的执行次数
暴力法分析
Sum = 0;
for(int i = 0;i < N;++i)
Sum++;
i → N i\rightarrow N i→N
- 时间复杂度为 O ( N ) O(N) O(N)
Sum = 0;
for(int i = 0;i < N;++i)
for(int j = 0;j < N;++j)
Sum++;
i → N j → N \begin{aligned} i\rightarrow N\\ j\rightarrow N \end{aligned} i→Nj→N
- 时间复杂度为 O ( N 2 ) O(N^2) O(N2)
Sum = 0;
for(int i = 0;i < N;++i)
for(int j = 0;j < N*N;++j)
Sum++;
i → N j → N 2 \begin{aligned} i\rightarrow N\\ j\rightarrow N^2 \end{aligned} i→Nj→N2
- 时间复杂度为 O ( N 3 ) O(N^3) O(N3)
Sum = 0;
for(int i = 0;i < N;++i)
for(int j = 0;j < i;++j)
Sum++;
i → N j → i → N \begin{aligned} i\rightarrow N\\ j\rightarrow i\rightarrow N \end{aligned} i→Nj→i→N
- 时间复杂度为 O ( N 2 ) O(N^2) O(N2)
Sum = 0;
for(int i = 0;i < N;++i)
for(int j = 0;j < i*i;++j)
for(int k = 0;k < j;++k)
Sum++;
i → N j → i ∗ i → N ∗ N k → j → N ∗ N \begin{aligned} i\rightarrow N\\ j\rightarrow i*i\rightarrow N*N\\ k\rightarrow j\rightarrow N*N \end{aligned} i→Nj→i∗i→N∗Nk→j→N∗N
- 时间复杂度为 O ( N 5 ) O(N^5) O(N5)
Sum = 0;
for(int i = 0;i < N;++i)
for(int j = 0;j < i*i;++j)
if(j % i==0)
for(int k = 0;k < j;++k)
Sum++;
i → N j → i ∗ i → N ∗ N k → j ( j % i = = 0 ) → i → N \begin{aligned} i\rightarrow N\\ j\rightarrow i*i\rightarrow N*N\\ k\rightarrow j(j\%i==0) \rightarrow i\rightarrow N \end{aligned} i→Nj→i∗i→N∗Nk→j(j%i==0)→i→N
- 时间复杂度为 O ( N 4 ) O(N^4) O(N4)
分治法
策略
- ”分“:将大问题大致分为两大致相等的 幂次阶 子问题,用递归求解
- “治”:将两个子问题的解合并到一起并可能再做些少量的附加工作(幂次阶),得到整个问题的解
主方法 :大小为
N
N
N 的原问题分成若干个大小为
N
b
\frac{N}{b}
bN 的子问题,其中
a
a
a 个子问题需要求解,而
c
N
k
cN^k
cNk 是合并各个子问题需要的工作量。此时问题可表示为:
T
(
N
)
=
{
a
0
N
=
1
a
T
(
N
b
)
+
c
N
k
N
>
1
T(N)=\begin{cases} a_0 & N=1\\ aT(\frac{N}{b}) + cN^k & N>1 \end{cases}
T(N)={a0aT(bN)+cNkN=1N>1
则其时间复杂度可相应的表示为:
T
(
N
)
=
{
O
(
N
l
o
g
b
a
)
a
>
b
k
O
(
N
k
l
o
g
b
N
)
a
=
b
k
O
(
N
k
)
a
<
b
k
T(N)=\begin{cases} O(N^{log_ba}) &a>b^k \\ O(N^klog_bN) &a=b^k \\ O(N^k) &a<b^k \end{cases}
T(N)=⎩
⎨
⎧O(Nlogba)O(NklogbN)O(Nk)a>bka=bka<bk
推导
已知
{ T ( 1 ) = 1 T ( N ) = 2 T ( N 2 ) + O ( N ) \begin{cases} T(1) = 1 \\ T(N) = 2T(\frac{N}{2}) + O(N) \end{cases} {T(1)=1T(N)=2T(2N)+O(N)
1. 等号右边连续代入递归关系
T
(
N
)
=
2
T
(
N
2
)
+
N
=
2
[
2
T
(
N
4
)
+
N
2
]
+
N
=
2
{
2
[
2
T
(
N
8
)
+
N
4
]
+
N
2
}
+
N
=
.
.
.
=
2
k
T
(
N
2
k
)
+
k
N
\begin{align} T(N) & = 2T(\frac{N}{2})+N \notag \\ &= 2[2T(\frac{N}{4})+\frac{N}{2}]+N \notag \\ & =2\{2[2T(\frac{N}{8})+\frac{N}{4}]+\frac{N}{2}\}+N \notag \\ & = ... \notag \\ & = 2^kT(\frac{N}{2^k}) + kN \notag \end{align}
T(N)=2T(2N)+N=2[2T(4N)+2N]+N=2{2[2T(8N)+4N]+2N}+N=...=2kT(2kN)+kN
由 k = l o g N k = logN k=logN 得
T ( n ) = N T ( 1 ) + N l o g N = N l o g ( N ) + N T(n) = NT(1)+NlogN = Nlog(N) + N T(n)=NT(1)+NlogN=Nlog(N)+N
2. 叠缩求和
用 N 去除递归关系中的两边,不断替换
T ( N ) N = T ( N 2 ) N 2 + 1 T ( N 2 ) N 2 = T ( N 4 ) N 4 + 1 T ( N 4 ) N 4 = T ( N 8 ) N 8 + 1 ⋮ ⋮ T ( 2 ) 2 = T ( 1 ) 1 + 1 \begin{align} \frac{T(N)}{N} &= \frac{T(\frac{N}{2})}{\frac{N}{2}} + 1 \notag \\ \notag \\ \frac{T(\frac{N}{2})}{\frac{N}{2}} &= \frac{T(\frac{N}{4})}{\frac{N}{4}} + 1 \notag \\ \notag \\ \frac{T(\frac{N}{4})}{\frac{N}{4}} &= \frac{T(\frac{N}{8})}{\frac{N}{8}} + 1 \notag \\ \notag \\ \vdots \notag \\ \vdots \notag \\ \notag \\ \frac{T(2)}{2} &= \frac{T(1)}{1} + 1\notag \\ \notag \\ \end{align} NT(N)2NT(2N)4NT(4N)⋮⋮2T(2)=2NT(2N)+1=4NT(4N)+1=8NT(8N)+1=1T(1)+1
将等号左边的所有相相加等于右边所有项的和,结果为
T ( N ) N = T ( 1 ) 1 + l o g N = N l o g ( N ) + N \begin{align} \frac{T(N)}{N} &= \frac{T(1)}{1} + logN \notag \\ \notag \\ &=Nlog(N) + N \notag \end{align} NT(N)=1T(1)+logN=Nlog(N)+N
3. 主方法
两个规模为 N 2 \frac{N}{2} 2N 的子问题,用 N 1 N^1 N1 的代价合并子问题
k = 1 , a = 2 , b = 2 k=1,a=2,b=2 k=1,a=2,b=2 , 2 = 2 1 , a = b k 2=2^1,a=b^k 2=21,a=bk
故由主定理, T ( N ) = O ( N l o g N ) T(N)=O(NlogN) T(N)=O(NlogN)
2.2.3 常见算法时间复杂度
| 描述 | 增长的数量级 | 说明 | 举例 |
|---|---|---|---|
| 常数级 | 1 | 普通语句 | 将两个数相加 |
| 对数级 | l o g N logN logN | 二分策略 | 二分查找 |
| 线性级 | N N N | 单层循环 | 找出最大元素 |
| 线性对数级 | N l o g N NlogN NlogN | 分治思想 | 归并排序 |
| 平方级 | N 2 N^2 N2 | 双层循环 | 检查所有元素对 |
| 立方级 | N 3 N^3 N3 | 三层循环 | 检查所有三元组 |
| 指数级 | 2 N 2^N 2N | 穷举查找 | 检查所有子集 |
2.3 最大子序列和问题求解
2.3.1 遍历所有子串,对子串的子序列依次求和
int MaxSubSequenceSum(const int A[],int N){
int ThisSum,MaxSum,i,j,k;
MaxSum = 0;
for(i = 0;i < N;++i){
for(j = 0;j <= i;++j){//遍历所有子串
ThisSum = 0;
for(k = 0;k <= j;++k)//当前子串的所有子序列求和
ThisSum += A[k];
if(ThisSum > MaxSum)
MaxSum = ThisSum;
}
}
return MaxSum;
}
i → N j → i → N k → j → N \begin{aligned} i\rightarrow N\\ j\rightarrow i\rightarrow N\\ k\rightarrow j\rightarrow N \end{aligned} i→Nj→i→Nk→j→N
- 时间复杂度为 O ( N 3 ) O(N^3) O(N3)
∑ i = 0 N − 1 ∑ j = 0 i ∑ k = 0 j 1 ∑ k = 0 j 1 = j + 1 ∑ j = 0 i j + 1 = ( i + 2 ) ( i + 1 ) 2 ∑ i = 0 N − 1 ( i + 2 ) ( i + 1 ) 2 = ∑ i = 1 N ( i + 1 ) i 2 = 1 2 ( ∑ i = 1 N i 2 + ∑ i = 1 N i ) = N 3 + 3 N 2 + 2 N 6 \begin{align} \sum_{i = 0}^{N-1}{\sum_{j = 0}^{i}{\sum_{k = 0}^{j}{1}}} \notag \\ \sum_{k = 0}^{j}{1} &= j+1 \notag \\ \sum_{j = 0}^{i}{ j+1} &= \frac{(i+2)(i+1)}{2} \notag \\ \\ \sum_{i = 0}^{N-1}{ \frac{(i+2)(i+1)}{2}} & = \sum_{i = 1}^{N}{ \frac{(i+1)i}{2}} \notag \\ \notag \\ &= \frac{1}{2}\left(\sum_{i=1}^{N}i^2+ \sum_{i=1}^{N}i\right)\\ \\ &= \frac{N^3+3N^2+2N}{6} \notag \end{align} i=0∑N−1j=0∑ik=0∑j1k=0∑j1j=0∑ij+1i=0∑N−12(i+2)(i+1)=j+1=2(i+2)(i+1)=i=1∑N2(i+1)i=21(i=1∑Ni2+i=1∑Ni)=6N3+3N2+2N
- 时间复杂度为 O ( N 3 ) O(N^3) O(N3)
2.3.2 记录中间累加量
∑ k = i j A k = A j + ∑ k = i j − 1 A k \sum_{k = i}^{j}{A_k} = A_j+\sum_{k = i}^{j-1}{A_k} k=i∑jAk=Aj+k=i∑j−1Ak
int MaxSubSequenceSum(const int A[],int N){
int ThisSum,MaxSum,i,j,k;
MaxSum = 0;
for(i = 0;i < N;++i){
ThisSum = 0;
for(j = 0;j <= i;++j){//遍历所有子串
ThisSum += A[k];
if(ThisSum > MaxSum){
MaxSum = ThisSum;
}
}
return MaxSum;
}
- 时间复杂度为 O ( N 2 ) O(N^2) O(N2)
2.3.3 分治法
将序列分成大致相等的两部分。
最大子序列和可能在三处出现:
数据的左半部分;
- 递归求解
数据的右半部分; - 递归求解
中间部分 - 分别求出前、后部分的最大和,相加中间部分最大和
int MaxSubSum(const int A[],int Left,int Right){
int MaxLeftSum,MaxRightSum;
int MaxLeftBorderSum,MaxRightBorderSum;
int LeftBorderSum,RightBorderSum;
int Center,i;
if(Left == Right){//只有一个元素
if(A[Left] > 0)//该元素非负即为最大和
return A[Left];
else{
return 0;
}
}
Center = (Left+Right) / 2;
MaxLeftSum = MaxSubSum(A,Left,Center);
MaxRightSum = MaxSubSum(A,Center,Right);
MaxLeftBorderSum = 0,LeftBorderSum = 0;
for(i = Center;i >= Left;i--){
LeftBorderSum += A[i];
if(LeftBorderSum > MaxLeftBorderSum)
MaxLeftBorderSum = LeftBorderSum;
}
MaxRightBorderSum = 0,RightBorderSum = 0;
for(i = Center;i >= Left;i--){
RightBorderSum += A[i];
if(RightBorderSum > MaxRightBorderSum)
MaxRightBorderSum = RightBorderSum;
}
return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum+MaxRightBorderSum);
}
int MaxSubSequenceSum(Const A[],int N){
return MaxSubSum(A,0,N-1);
}
{ T ( 1 ) = 1 T ( N ) = 2 T ( N / 2 ) + O ( N ) \begin{cases} T(1) = 1 \\ T(N) = 2T(N/2) + O(N) \end{cases} {T(1)=1T(N)=2T(N/2)+O(N)
- 时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)
分治法 时间复杂度一般都是若干个代价为 l o g N logN logN 的子问题与一个处理函数的代价和
2.3.4 最简
int MaxSubSequenceSum(const int A[],int N){
int ThisSum,MaxSum,j;
ThisSum = MaxSum = 0;
for(j = 0;j < N;++j){
ThisSum += A[k];
if(ThisSum > MaxSum){
MaxSum = ThisSum;
}else if(ThisSum < 0){
ThisSum = 0;
}
}
return MaxSum;
}
- 时间复杂度为 O ( N ) O(N) O(N)
2.4 空间复杂度
算法所需的辅助空间数量级
- 运行过程中变量占用的空间 辅助数组
- 递归工作栈 递归深度
原地工作
算法所需的辅助空间为常量
2.5 习题
2.1


2.2


T ( N ) = O ( N ) T(N)=O(N) T(N)=O(N) , O ( N ) O(N) O(N) 是上界,但不是上确界,即 T ( N ) = a N + b = O ( N 2 ) = O ( N 3 ) T(N)=aN+b=O(N^2)=O(N^3) T(N)=aN+b=O(N2)=O(N3)
即 lim n → ∞ f ( N ) T 1 ( N ) = ∞ \lim_{n\rightarrow \infty}\limits \frac{f(N)}{T_1(N)}=\infty n→∞limT1(N)f(N)=∞ ,且 lim n → ∞ f ( N ) T 2 ( N ) = ∞ \lim_{n\rightarrow \infty}\limits \frac{f(N)}{T_2(N)}=\infty n→∞limT2(N)f(N)=∞ ,无法判断 T 1 ( N ) T_1(N) T1(N) 与 T 2 ( N ) T_2(N) T2(N) 的关系
2.3

定理: l o g k N log^kN logkN 的增长率远小于 N ϵ N^\epsilon Nϵ 的增长率, l o g k N = o ( N ) log^kN=o(N) logkN=o(N)
实际上是比较
l
o
g
N
logN
logN 与
N
ϵ
l
o
g
N
N^{\frac{\epsilon}{\sqrt{logN}}}
NlogNϵ
l
o
g
l
o
g
N
与
ϵ
l
o
g
N
l
o
g
N
=
ϵ
l
o
g
N
的比较,令
L
=
l
o
g
N
l
o
g
L
2
=
2
l
o
g
L
与
ϵ
L
,
可见
L
的增长率大于
l
o
g
L
的增长率
即
N
l
o
g
N
的增长率小于
N
1
+
ϵ
l
o
g
N
\begin{aligned} &loglogN与\frac{\epsilon}{\sqrt{logN}}logN=\epsilon\sqrt{logN}的比较,令L=\sqrt{logN}\\ &logL^2=2logL与\epsilon L,可见 L的增长率大于logL的增长率\\ &即 NlogN的增长率小于 N^{1+\frac{\epsilon}{\sqrt{logN}}} \end{aligned}
loglogN与logNϵlogN=ϵlogN的比较,令L=logNlogL2=2logL与ϵL,可见L的增长率大于logL的增长率即NlogN的增长率小于N1+logNϵ
2.5
可以理解为 f ( N ) f(N) f(N) 的增长率不大于 g ( N ) g(N) g(N) 的增长率, g ( N ) g(N) g(N) 的增长率也不大于 f ( N ) f(N) f(N) 的增长率
即 f ( N ) f(N) f(N) 的增长率与 g ( N ) g(N) g(N) 的增长率相等即可 f ( N ) = Θ ( g ( N ) ) f(N)=\Theta(g(N)) f(N)=Θ(g(N))
2.6 在前面已经应用举例
2.5.7 随机数序列生成算法

alg1
void randSeq(int A[],int N){
int i = 0;
while(i < N){
int ran = randInt(0,N);
for(k = 0;k < i;k++){
if(A[k] == ran)
break;
}
if(k == i){
A[i] = ran;
i++;
}
}
}
生成第
i
i
i 个不重复随机数的概率为
N
−
i
N
\frac{N-i}{N}
NN−i ,所以理论上经过
N
N
−
i
\frac{N}{N-i}
N−iN 次生成得到不重复随机数的概率为
1
1
1 ,对于每个随机数需要经过
i
i
i 次验证,所以总耗时
∑
i
=
0
N
−
1
N
N
−
i
i
<
∑
i
=
0
N
−
1
N
2
N
−
i
=
N
2
∑
i
=
0
N
−
1
1
N
−
i
=
N
2
∑
j
=
1
N
1
j
<
N
2
l
o
g
ϵ
N
=
O
(
N
2
l
o
g
N
)
\begin{aligned} \sum_{i=0}^{N-1}\frac{N}{N-i}i<\sum_{i=0}^{N-1}\frac{N^2}{N-i}=N^2\sum_{i=0}^{N-1}\frac{1}{N-i}=N^2\sum_{j=1}^{N}\frac{1}{j}<N^2log_\epsilon N=O(N^2logN) \end{aligned}
i=0∑N−1N−iNi<i=0∑N−1N−iN2=N2i=0∑N−1N−i1=N2j=1∑Nj1<N2logϵN=O(N2logN)
alg2
void ranSeq(int A[],int N){
int used[MAX_INT] = {0};
int i = 0;
while(i < N){
ran = ranInt(0,N);
if(used[ran] == 0){
A[i] = ran;
used[ran] = 1;
i++;
}
}
}
省去了对每个随机生成的数进行
i
i
i 次验证,总的时间复杂度为
∑
i
=
0
N
−
1
N
N
−
i
<
∑
i
=
0
N
−
1
N
N
−
i
=
N
∑
i
=
0
N
−
1
1
N
−
i
=
N
∑
j
=
1
N
1
j
<
N
l
o
g
ϵ
N
=
O
(
N
l
o
g
N
)
\begin{aligned} \sum_{i=0}^{N-1}\frac{N}{N-i}<\sum_{i=0}^{N-1}\frac{N}{N-i}=N\sum_{i=0}^{N-1}\frac{1}{N-i}=N\sum_{j=1}^{N}\frac{1}{j}<Nlog_\epsilon N=O(NlogN) \end{aligned}
i=0∑N−1N−iN<i=0∑N−1N−iN=Ni=0∑N−1N−i1=Nj=1∑Nj1<NlogϵN=O(NlogN)
alg3
void ranSeq(int A[],int N){
for(int i = 0;i < N;++i)
A[i] = i+1;
for(int i = 0;i < N;++i)
swap(&A[i],&A[randInt(0,i)]);
}
时间复杂度是线性的 O ( N ) O(N) O(N)
2.5.9 多项式计算
计算多项式
F
(
x
)
=
∑
i
=
0
N
A
i
X
i
F(x)=\sum_{i=0}^{N}\limits A_iX^i
F(x)=i=0∑NAiXi 需要多长时间
简单方法取幂:
void poly(int A[],int X,int N){
int res = A[0];
for(int i = 1;i <= N;++i){
res += A[i]*pow(X,i);//时间复杂度为O(N)
}
return res;
}
快速幂
void poly(int A[],int X,int N){
int res = A[0];
for(int i = 1;i <= N;++i){
res += A[i]*pow(X,i);//快速幂,时间复杂度为O(logN)
}
return res;
}
- 时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)
秦九韶算法(Horner算法)
void poly(int A[],int X,int N){
int res = 0;
for(int i = N;i >= 0;--i){
res = A[i] + X*res;
}
return res;
}
- 时间复杂度为 O ( N ) O(N) O(N)
oid poly(int A[],int X,int N){
int res = A[0];
for(int i = 1;i <= N;++i){
res += A[i]*X;
}
return res;
}
- 时间复杂度为 O ( N ) O(N) O(N)
2.5.11 在有序数组中查找是否存在整数——二分查找
时间复杂度 O ( l o g N ) O(logN) O(logN)
2.5.13 判断一个正整数是否为素数
素数定义:在大于1的自然数中,除了1和他本身之外不再有其他因数的自然数
- 可见偶数一定不是素数——可被2整除
alg1
直接判断,对一个自然数 k 来说,需要判断 k-2 次,时间复杂度为
O
(
n
)
O(n)
O(n)
bool IsPrime(int n){
if(n == 1)
return false;
for(int i = 2;i < n-1;++i){
if(n % i == 0)
return false;
}
return true;
}
alg2
除了1之外,任何合数最小的因子就是2,相应的最大因子就是 ⌈ n 2 ⌉ \lceil \frac{n}{2}\rceil ⌈2n⌉ ,所以只需要从2开始遍历到 ⌈ n 2 ⌉ \lceil \frac{n}{2}\rceil ⌈2n⌉ 就可以了
bool IsPrime(int n){
if(n == 1)
return false;
for(int i = 2;i < n/2+1;++i){
if(n % i == 0)
return false;
}
return true;
}
- 循环判断条件必须包含
n
2
\frac{n}{2}
2n :如
n
=
4
n=4
n=4 时,必须通过
%
2
\%2
%2 判断为素数,若
<
2
<2
<2 则会出现错误的结果
- 可以是
i <= n/2或i < n/2 + 1
- 可以是
时间复杂度仍然为 O ( n ) O(n) O(n)
alg3
根据素数定义,如果一个数不是素数,即合数一定是两个数的乘积
假设 n = i ∗ j n=i*j n=i∗j ,则一定有一个 ≤ n \le \sqrt{n} ≤n ,另一个 n \sqrt{n} n ,因此只看较小那个数存不存在就可以判断n是否为素数
bool IsPrime(int n){
if(n == 1)
return false;
for(int i = 2;i < n/2+1;++i){
if(n % i == 0)
return false;
}
return true;
}
时间复杂度降为 O ( N ) O(\sqrt{N}) O(N)
- 当然,可以针对 alg1,alg2,alg3 做进一步改进,
i++改为i+=2,因为我们知道偶数一定不是素数
习题13是根据这种做法设问的
(b) O ( N ) O(\sqrt{N}) O(N)
© 令B表示N的二进制中的位数,则B的值为多少
N
=
2
B
−
1
x
B
−
1
+
2
B
−
2
x
B
−
2
+
⋯
+
2
0
x
0
,
x
i
=
0
,
1
表示是否取该位
\begin{aligned} N=2^{B-1}x_{B-1}+2^{B-2}x_{B-2}+\cdots+2^0x_0,x_i=0,1表示是否取该位 \end{aligned}
N=2B−1xB−1+2B−2xB−2+⋯+20x0,xi=0,1表示是否取该位
故
N
=
O
(
2
B
)
N=O(2^B)
N=O(2B) ,
B
=
O
(
l
o
g
N
)
B=O(logN)
B=O(logN)
(d)用B表示时间复杂度
O ( N 1 2 ) = O ( 2 B 1 2 ) = O ( 2 B 2 ) O(N^{\frac{1}{2}})=O(2^{B\frac{1}{2}})=O(2^{\frac{B}{2}}) O(N21)=O(2B21)=O(22B)
(e)比较确定20位二进制的数是否为素数与40位的运行时间
令 T T T 表示确定20位二进制的数是否为素数的运行时间,有 T = O ( 2 20 2 ) T=O(2^\frac{20}{2}) T=O(2220) ,有判断40位二进制数是否为二进制数的时间为 T 2 T^2 T2
alg4
查表
表构造原理:如果一个数不能整除比它小的任何素数,那么这个数就是素数
等价于证明:“不能被素数整除则一定不能被合数整除”逆否“能被合数整除则一定能被素数整除”
-
合数要么是偶数,要么是奇合数
- 对于奇合数,只能被 > 2 >2 >2 的素数整除(若有偶因数,则成为偶数)
- 对于偶数,一定能分解为 2 × p 1 × ⋯ × p k 2\times p_1\times\cdots \times p_k 2×p1×⋯×pk ,p的取值为 2 , 3 , 5 , 7 , 11 , 13 , . . 2,3,5,7,11,13,.. 2,3,5,7,11,13,.. 等一系列素数
可见,如果一个数是合数,则一定能被素数整除,故不能被比他小的任何素数整除,一定是素数
//n:输入的要查找的数
//count:当前已知的小于等于sqrt{n}的素数个数
//Prime:存放素数的数组
bool IsPrime(int n, int count, int* Prime) {
int i = 0;
for (i = 0;i < count;i++) {
//只需要判断到sqrt{n},上述定理适用
if (n % Prime[i] == 0)
return false;
}
return true;
}
alg4——普通筛法(埃拉托斯特尼筛Eratosthenes法)构造素数数组
只关注下标为 2 ∼ n 2\sim n 2∼n 的数组元素,如果该元素为1,则说明数组元素对应的下标为素数——桶思维
假设所有元素都是素数,初始化为1,遍历范围为 2 ∼ n 2\sim \sqrt{n} 2∼n ,将已知素数的整数倍下标赋值为0,
-
要得到自然数n以内的全部素数,必须把不大于n的所有素数的倍数剔除,剩下的就是素数

//isprime:判断素数的数组 上限N
//Prime[]元素为素数,count为Prime大小
void Eratprime(int* isprime, int n,int *Prime,int &count) {
int i = 0;
int j = 0;
if(isprime != NULL){//确保isPrime不是空指针
//初始化isprime
for (i = 2; i <= (int)sqrt(n); i++)
isprime[i] = 1;
}
for (i = 2;i <= (int)sqrt(n); i++) {
for (j = 2; i * j <= n; j++) {//素数的n倍(n >= 2)不是素数
isprime[i * j] = 0;
}
}
count = 0;
for(i = 0;i <= (int)sqrt(n);++i){
if(isprime[i] == 1){
Prime[count] = i;
count++;
}
}
}
int main(){
int n;
cin >> n;
int *Prime = (int *)malloc((sqrt(n)+1)*sizeof(int));
int *isprime = (int *)malloc(n*sizeof(int));
int count = 0;
Eratprime(isprime,n,Prime,count);
for(int p = 0;p < count;++p)
cout << *(Prime+p) << endl;
cout << boolalpha << IsPrime(n,count,Prime);
return 0;
}
- 埃拉斯托拉斯筛法,确定小于n的所有素数,时间复杂度为
O
(
N
l
o
g
l
o
g
N
)
O(NloglogN)
O(NloglogN)
- 而判断n是否为素数,我们实际上之关心小于 N \sqrt{N} N 的所有素数,所以可优化为 O ( N ) O(N) O(N)
alg5——找n以内的所有素数线性筛法——欧拉筛法
在提出非素数时,有些合数会重复,如:
-
2是素数,剔除”2 的倍数“,他们是:4,
6, 8,10,12, 14, 16 -
3是素数,剔除”3 的倍数”,他们时,
6,9,12,156,12是重复的。
合数一定有一个最小的质因子,所以在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的
void Eulerprime(int* isprime, int n,int *Prime,int &count) {
//从2遍历到范围上限N
for(i = 2; i <= N; i++) {
if(isPrime[i])//如果下标(下标对应着1 ~ 范围上限N)对应的isPrime值没有被置为false,说明这个数是素数,将下标放入素数数组
Prime[count++] = i;
//循环控制表达式的意义:j小于等于素数数组的个数 或 素数数组中的每一个素数与 i 的积小于范围上限N
for(j = 0; j < count && Prime[j] * i <= N; j++){
isPrime[i * Prime[j]] = false;//每一个素数的 i 倍(i >= 2)都不是素数,置为false
//这个是欧拉筛法的核心,它可以减少非素数置false的重复率
//通过这个最小质因子就可以判断什么时候不用继续筛下去了。
if(i % Prime[j] == 0)
break;
//比如 i=6,prime[j]=2(这时候 prime已经有了2,3,5),
//i%prime[j]==0,所以就可以跳出循环。
}
}
}
- 欧拉筛获取n以内的所有素数,时间复杂度为
O
(
N
)
O(N)
O(N)
- 若只关心n是否为素数,可以只获取 N \sqrt{N} N 内的素数,时间复杂度减少为 O ( N ) O(\sqrt{N}) O(N)
alg6——六素数法
任何一个自然数都可以被写成
x
=
6
k
=
6
×
k
x
=
6
k
+
1
x
=
6
k
+
2
=
2
×
(
3
k
+
1
)
x
=
6
k
+
3
=
3
×
(
2
k
+
1
)
x
=
6
k
+
4
=
2
×
(
3
k
+
2
)
x
=
6
k
+
5
\begin{aligned} &x=6k=6\times k\\ &x=6k+1\\ &x=6k+2=2\times (3k+1)\\ &x=6k+3=3\times(2k+1)\\ &x=6k+4=2\times (3k+2)\\ &x=6k+5\\ \end{aligned}
x=6k=6×kx=6k+1x=6k+2=2×(3k+1)x=6k+3=3×(2k+1)x=6k+4=2×(3k+2)x=6k+5
中的一个。
可见,在6的倍数附近,可能会出现两个素数 6 k − 1 6k-1 6k−1 和 6 k + 1 6k+1 6k+1 。故判断一个数是否为素数,取余即可
例外:
2,3,5,7,11,13 ,17,19,23,29,31,37,41,43,47,53,59,61
- 可见,有两种例外,25,35对5取余为0,39对3取余为0,49对7取余为0
所以对素数判断的改进思路为:
-
在 alg1 的基础上,将步长改为6
-
还是根据没有素因数则为素数的定理,只不过不需要构造素数表
判断小于 n \sqrt{n} n 范围内,能否被相邻两个可能的素数是否能整除n即可
bool IsPrime(int n){
if(n <= 1)
return false;
if(n == 2 || n == 3)
return true;
if(n % 2 == 0 || n % 3 == 0)
return false;
for(int i = 5; i < (int)sqrt(n)+1; i += 6 ){
if( n % i == 0 || n % (i+2) == 0 ){
return false;
}
}
return true;
}
2.15 证明8次乘法可算出
X
62
X^{62}
X62
X
2
=
X
⋅
X
X
4
=
X
2
⋅
X
2
X
8
=
X
4
⋅
X
4
X
10
=
X
8
⋅
X
2
X
20
=
X
10
⋅
X
10
X
40
=
X
20
⋅
X
20
X
60
=
X
40
⋅
X
20
X
62
=
X
60
⋅
X
2
X^2=X\cdot X\\ X^4=X^2\cdot X^2\\ X^8=X^4\cdot X^4\\ X^{10}=X^{8}\cdot X^2\\ X^{20}=X^{10}\cdot X^{10}\\ X^{40}=X^{20}\cdot X^{20}\\ X^{60}=X^{40}\cdot X^{20}\\ X^{62}=X^{60}\cdot X^{2}
X2=X⋅XX4=X2⋅X2X8=X4⋅X4X10=X8⋅X2X20=X10⋅X10X40=X20⋅X20X60=X40⋅X20X62=X60⋅X2
2.16 非递归形式求快速幂
2.17 快速幂的乘法精确次数
见快速幂部分
2.18


d感觉是不能