文章目录
- (简单)232. 用栈实现队列
- (简单)225. 用队列实现栈
- (简单)20. 有效的括号
- (简单)1047. 删除字符串中的所有相邻重复项
- (中等)150. 逆波兰表达式求值
- (困难)239. 滑动窗口最大值
- (中等)347. 前K个高频元素
(简单)232. 用栈实现队列
用两个栈模拟队列
import java.util.Stack;
class MyQueue {
private Stack<Integer> s1;
private Stack<Integer> s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
public void push(int x) {
while (!s2.isEmpty()) {
s1.push(s2.pop());
}
s1.push(x);
}
public int pop() {
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
return s2.pop();
}
public int peek() {
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
return s2.peek();
}
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/
另一种写法
import java.util.Stack;
class MyQueue {
private Stack<Integer> inStack;
private Stack<Integer> outStack;
public MyQueue() {
inStack = new Stack<>();
outStack = new Stack<>();
}
public void push(int x) {
inStack.push(x);
}
public int pop() {
if (outStack.isEmpty()) {
in2out();
}
return outStack.pop();
}
public int peek() {
if (outStack.isEmpty()) {
in2out();
}
return outStack.peek();
}
public boolean empty() {
return inStack.isEmpty() && outStack.isEmpty();
}
private void in2out() {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/
来自代码随想录:代码开发上的习惯问题,在工业级别代码开发中,最忌讳的就是实现一个类似的函数,直接把代码粘贴过来改一改就完事了。
这样的项目代码会越来越乱,一定要懂得复用,功能相近的函数要抽象出来,不要大量的复制粘贴,很容易出问题。
工作中如果发现某一个功能自己要经常用,同事们可能也会用到,自己就花时间把这个功能抽象成一个好用的函数或者工具类,不仅方便自己,也方便他人。
(简单)225. 用队列实现栈
我的思路,没有按照题目要求使用两个队列实现栈,只使用了一个队列(双端队列)
import java.util.Deque;
import java.util.LinkedList;
class MyStack {
private Deque<Integer> deque;
public MyStack() {
deque = new LinkedList<>();
}
public void push(int x) {
deque.addLast(x);
}
public int pop() {
return deque.pollLast();
}
public int top() {
return deque.peekLast();
}
public boolean empty() {
return deque.isEmpty();
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列来实现栈的操作,其中queue1用于存储栈内的元素,queue2作为入栈操作的辅助队列。
入栈操作时,首先将元素入队到queue2,然后将queue1的全部元素依次出队并入队到queue2,此时queue2的前端的元素即为新入栈的元素,再将queue1和queue2互换,则queue1的元素即为栈内的元素,queue1的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保queue1的前端元素为栈顶元素,因此出栈操作和获取栈顶操作都可以简单实现。出栈操作只需要移除queue1的前端元素并返回即可,获取栈顶元素操作只需要获得queue1的前端元素并返回即可。
由于queue1用于存储栈内的元素,判断栈是否为空时,只需要判断queue1是否为空即可。
import java.util.LinkedList;
import java.util.Queue;
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
public void push(int x) {
queue2.add(x);
while (!queue1.isEmpty()) {
queue2.add(queue1.poll());
}
Queue<Integer> tmp = queue1;
queue1 = queue2;
queue2 = tmp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty();
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
复杂度分析:
- 时间复杂度:入栈操作O(n),其余操作都是O(1),因为n是栈内的元素个数
- 入栈操作需要将queue1中的n个元素出队,并入队n+1个元素到queue2,共有2n+1次操作(首先是最新那一个元素入队queue2,n个元素从queue1出队,然后n个元素再入队queue2),因此入栈操作的时间复杂度是O(n)
- 出栈操作对应将queue1的前端元素出队,时间复杂度是O(1)
- 获得栈顶元素操作对应获取queue1的前端元素,时间复杂度是O(1)
- 判断栈是否为空操作只需要判断queue1是否为空,时间复杂度O(1)
- 空间复杂度:O(n),其中n是栈内元素的个数。需要使用两个队列存储栈内的元素。
只使用一个队列来模拟栈
使用一个队列时,为了满足栈的特性,即最后入栈的元素最先出栈,同样需要满足队列前端的元素是最后入栈的元素。
入栈操作:首先获得入栈前的元素个数n,然后将元素入队到队列,再将队列中的前n个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端的元素即为新入栈的元素,且队列的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保队列的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可,获得栈顶元素操作只需要获得队列的前端元素并返回即可(不移除元素)。
import java.util.LinkedList;
import java.util.Queue;
class MyStack {
Queue<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) {
int n = queue.size();
queue.add(x);
for (int i = 0; i < n; i++) {
queue.add(queue.poll());
}
}
public int pop() {
return queue.poll();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
复杂度分析:
- 时间复杂度:入栈操作O(n),其余操作都是O(1),其中n是栈内的元素个数
- 空间复杂度:O(n),其中n是栈内的元素个数。需要使用一个队列存储栈内的元素
(简单)20. 有效的括号
我的思路:使用栈结构,如果当前遍历到的是括号的左半边,则存入栈中,如果当前遍历到的是括号的右半边,那么就和栈顶元素匹配,如果能匹配上则弹出栈顶元素,继续遍历下一个,如果不匹配,则返回false;如果当前遍历到的是括号的右半边,并且栈为空,也返回false,说明前面没有与之匹配的左半边括号。
import java.util.Stack;
class Solution {
public boolean isValid(String s) {
char[] chars = s.toCharArray();
Stack<Character> stack = new Stack<>();
for (char c : chars) {
if (c == '(' || c == '{' || c == '[') {
stack.push(c);
} else if (!stack.isEmpty()) {
if (c == ']' && stack.peek() == '[') {
stack.pop();
} else if (c == '}' && stack.peek() == '{') {
stack.pop();
} else if (c == ')' && stack.peek() == '(') {
stack.pop();
} else {
return false;
}
} else {
return false;
}
}
return stack.isEmpty();
}
}
官方给出了更详细的解释:
当遍历给定的字符串时,当遇到一个左括号时,会期望在后续的遍历中有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合,因此可以将这个左括号放入栈顶。
当遇到一个右括号时,需要将一个相同类型的左括号闭合。此时,取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同类型,或者栈中没有左括号,那么字符串s无效,返回false。
为了快速判断括号的类型,使用哈希表存储每一种括号。哈希表的键为右括号,值为相同类型的左括号。
在遍历结束后,如果栈中没有左括号,说明字符串s中所有左括号闭合,返回true,否则返回false。
注意,有效字符串的长度一定是偶数,如果字符串的长度为奇数,直接返回false。
import java.util.HashMap;
import java.util.Stack;
class Solution {
public boolean isValid(String s) {
if ((s.length() & 1) == 1) {
return false;
}
char[] chars = s.toCharArray();
Stack<Character> stack = new Stack<>();
HashMap<Character, Character> map = new HashMap<Character, Character>() {{
put(')', '(');
put(']', '[');
put('}', '{');
}};
for (char c : chars) {
//当前c是右括号
if (map.containsKey(c)) {
if (stack.isEmpty() || stack.peek() != map.get(c)) {
//栈为空,或者匹配不上
return false;
}
stack.pop();
} else {
//c是左括号
stack.push(c);
}
}
return stack.isEmpty();
}
}
复杂度分析:
- 时间复杂度:O(n),其中n是字符串的长度
- 空间复杂度:O(n+| ∑ \sum ∑|),其中 ∑ \sum ∑表示字符集,本题中字符集串只包含6种括号,| ∑ \sum ∑|=6,栈中的字符数量为O(n),而哈希表使用的空间为O(| ∑ \sum ∑|),相加即可得到总空间复杂度
(简单)1047. 删除字符串中的所有相邻重复项
使用栈去模拟,如果当前字符与栈顶元素相同,则弹出,如果不相同则加入栈中,最后符合条件的字符都会存储在栈中,但是栈的特点是先进后出,所以使用StringBuilder,总是在首位插入字符,还原字符串原来的顺序
import java.util.Stack;
class Solution {
public String removeDuplicates(String s) {
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
if (!stack.isEmpty() && c == stack.peek()) {
stack.pop();
} else {
stack.push(c);
}
}
StringBuilder stringBuilder = new StringBuilder();
while (!stack.isEmpty()) {
stringBuilder.insert(0, stack.pop());
}
return stringBuilder.toString();
}
}
官方解答
当字符串中同时有多组相邻重复项时,我们无论先删除哪一个,都不会影响最终的结果。所以,从左向右顺次处理该字符串即可。
消除一对相邻重复项可能会导致新的相邻重复项出现。所以,需要保存当前还未被删除的字符。用栈是比较合适的。只需要遍历该字符串,如果当前字符和栈顶字符相同,就贪心地将其消去,否则就将其入栈即可。
对于Java语言,String类没有提供相应的接口,则需要在遍历完成字符串后,使用栈中的字符显式地构造出需要被返回的字符串。
用StringBuilder来模拟栈
class Solution {
public String removeDuplicates(String s) {
StringBuilder stack = new StringBuilder();
int top = -1;
for (char c : s.toCharArray()) {
if (top >= 0 && stack.charAt(top) == c) {
stack.deleteCharAt(top);
--top;
} else {
stack.append(c);
++top;
}
}
return stack.toString();
}
}
(中等)150. 逆波兰表达式求值
我的思路:如果是数字的话,就压入栈中,如果是操作符,就取出栈中的两个元素,注意,加法和乘法,哪一个数字在前,哪一个数字在后没有区别,对于减法和除法来说还是有区别的。先取出来的数字在是要放在操作符的右边,而后取出来的需要放在操作符的左边
import java.util.Stack;
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < tokens.length; i++) {
if ("+".equals(tokens[i]) || "-".equals(tokens[i]) || "*".equals(tokens[i]) || "/".equals(tokens[i])) {
Integer i2 = stack.pop();
Integer i1 = stack.pop();
switch (tokens[i]) {
case "+":
stack.push(i1 + i2);
break;
case "-":
stack.push(i1 - i2);
break;
case "*":
stack.push(i1 * i2);
break;
case "/":
stack.push(i1 / i2);
break;
}
} else {
stack.push(Integer.valueOf(tokens[i]));
}
}
return stack.peek();
}
}
复杂度分析:
- 时间复杂度:O(n),其中n是tokens的长度。需要遍历数组tokens一次,计算逆波兰表达式的值
- 空间复杂度:O(n),其中n是数组tokens的长度。使用栈存储计算过程中的数,栈内元素个数不会超过逆波兰表达式的长度
官方其他思路,使用数组模拟
使用一个数组模拟栈操作。
使用数组代替栈,需要预先定义数组的长度。对于长度为n的逆波兰表达式,显然栈内元素个数不会超过n,但是将数组的长度定义为n仍然超过了栈内元素个数的上界。
对于一个有效的逆波兰表达式,其长度n一定是奇数,且操作数的个数一定比运算符的个数多1个。考虑遇到操作数和运算符时,栈内元素个数如何变化:
- 如果遇到操作数,则将操作数入栈,因此栈内元素增加1个
- 如果遇到运算符,则将两个操作数出栈,然后将一个新操作数入栈,因此栈内元素先减少2个再增加1个,结果是栈内元素减少1个
对于一个有效的逆波兰表达式,其长度n一定是奇数,且操作数的个数一定比运算符个数多1个,即包含 n + 1 2 \frac{n+1}{2} 2n+1个操作数和 n − 1 2 \frac{n-1}{2} 2n−1个运算符。
最坏情况下, n + 1 2 \frac{n+1}{2} 2n+1个操作数都在表达书的前面, n − 1 2 \frac{n-1}{2} 2n−1个运算符都在表达式后面,因此栈内元素最多为 n + 1 2 \frac{n+1}{2} 2n+1。所以定义数组长度是 n + 1 2 \frac{n+1}{2} 2n+1。
class Solution {
public int evalRPN(String[] tokens) {
int n = tokens.length;
int[] stack = new int[(n + 1) / 2];
int index = -1;
for (int i = 0; i < n; i++) {
switch (tokens[i]) {
case "+":
--index;
stack[index] += stack[index + 1];
break;
case "-":
--index;
stack[index] -= stack[index + 1];
break;
case "*":
--index;
stack[index] *= stack[index + 1];
break;
case "/":
--index;
stack[index] /= stack[index + 1];
break;
default:
++index;
stack[index] = Integer.parseInt(tokens[i]);
}
}
return stack[index];
}
}
复杂度分析:
- 时间复杂度:O(n),其中n是tokens的长度。需要遍历数组tokens一次,计算逆波兰表达式的值。
- 空间复杂度:O(n),其中n是数组tokens的长度。需要创建长度为 n + 1 2 \frac{n+1}{2} 2n+1的数组模拟栈操作。
(困难)239. 滑动窗口最大值
官方思路
对于每个滑动窗口,可以使用O(k)的时间遍历其中的每一个元素,找出其中的最大值。对于长度为n的数组nums而言,窗口的数量为n-k+1,因此算法的时间复杂度是O((n-k+1)k)=O(nk),会超出时间限制,因此需要进一步优化。
方法一,优先队列
对于【最大值】,使用优先队列,其中的大根堆可以帮助我们实现维护一系列元素中的最大值。
对于本题,初始时,将数组nums的前k个元素放入优先队列中。每当向右移动窗口时,就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值并不在滑动窗口中,在这种情况下,这个值在数组nums中的位置出现在滑动窗口的左边界的左侧。因此,当我们继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,可以将这个数永久地从优先队列中移除。
不断地移动堆顶的元素,直到其确定出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,可以在优先队列中存储二元组(num,index),表示元素num在数组中的下标为index。
根据上述思路,我的代码如下,优先队列中的每一个元素是一个长度为2的数组,下标为0的位置存放的是具体值,下标为1的位置存放该值在nums数组中的下标
import java.util.Comparator;
import java.util.PriorityQueue;
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
PriorityQueue<int[]> queue = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o2[0] - o1[0];
}
});
int n = nums.length;
int[] res = new int[n - k + 1];
for (int i = 0; i < k; i++) {
queue.add(new int[]{nums[i], i});
}
res[0] = queue.peek()[0];
for (int i = k; i < n; i++) {
while (!queue.isEmpty() && i - queue.peek()[1] >= k) {
queue.poll();
}
queue.add(new int[]{nums[i], i});
res[i - k + 1] = queue.peek()[0];
}
return res;
}
}
复杂度分析:
- 时间复杂度:O(nlogn),其中n是数组nums的长度。在最坏的情况下,数组nums中的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度是O(logn),因此总的时间复杂度为O(nlogn)。
- 空间复杂度:O(n),即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的O(n)空间,只计算额外的空间使用。
方法二,单调队列
顺着方法一的思路,继续优化。
目标是为了求出滑动窗口的最大值,假设当前的滑动窗口中有两个下标i和j,其中i在j的左侧(i<j)
当滑动窗口向右移时,只要i还在窗口中,j一定也还在窗口中,这是i在j的左侧所保证的。因此,由于nums[j]的存在,nums[i]一定不会是滑动窗口中的最大值,可以将nums[i]永久移除。
使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在nums中对应的值是严格单调递减的。这也就保证了队首的元素一定是当前滑动窗口中的最大值的下标。
当滑动窗口向右移时,需要把一个新的元素放入队列中。为了保持队列的性质,会不断地将新的元素与队尾元素比较,如果前者大于等于后者,则将队尾的元素永久地移除。需要不断进行此操作,直到队列为空或者新的元素小于队尾地元素。
由于队列中的下标对应的元素时严格单调递减的,因此此时队首下标对应地元素就是滑动窗口中的最大值。但是,随着窗口不断地右移,可能当前队首元素已经不在滑动窗口中了,所以需要判断,弹出不在窗口中的元素。
为了可以同时弹出队首和队尾元素,需要使用双端队列。满足这种单调性的队列叫单调队列。
import java.util.LinkedList;
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
LinkedList<Integer> list = new LinkedList<>();
for (int i = 0; i < k; i++) {
while (!list.isEmpty() && nums[list.peekLast()] <= nums[i]) {
list.pollLast();
}
list.addLast(i);
}
int n = nums.length;
int[] res = new int[n - k + 1];
res[0] = nums[list.peekFirst()];
for (int i = k; i < n; i++) {
while (!list.isEmpty() && nums[list.peekLast()] <= nums[i]) {
list.pollLast();
}
list.addLast(i);
while (i - list.peekFirst() >= k) {
list.pollFirst();
}
res[i - k + 1] = nums[list.peekFirst()];
}
return res;
}
}
(中等)347. 前K个高频元素
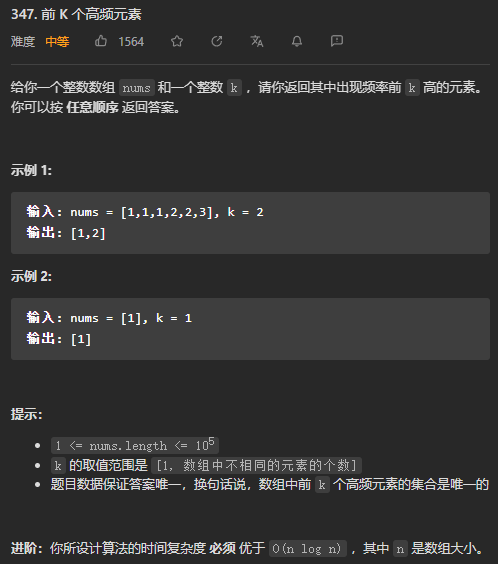
我的思路,使用HashMap来存储数组中的数以及这个数出现的次数,最后按照value来从大到小排序,取出前k个项的key值保存在数组中返回
class Solution {
public int[] topKFrequent(int[] nums, int k) {
HashMap<Integer, Integer> map = new HashMap<>();
int n = nums.length;
for (int i = 0; i < n; i++) {
map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
}
ArrayList<Map.Entry<Integer, Integer>> list = new ArrayList<>(map.entrySet());
Collections.sort(list, (o1, o2) -> o2.getValue() - o1.getValue());
int[] res = new int[k];
for (int i = 0; i < k; i++) {
res[i] = list.get(i).getKey();
}
return res;
}
}
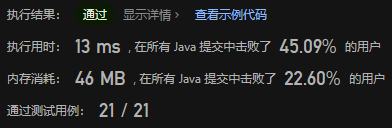
不过这种给HashMap排序的方法,由于可能有O(N)个不同的出现次数(其中N为原数组的长度),故总的算法复杂度会达到O(NlogN),不满足题目要求。
使用堆的思想:建立一个小顶堆,然后遍历【出现次数数组】
- 如果堆中的元素个数小于k,就可以直接插入堆中
- 如果堆中的元素个数等于k,则检查堆顶与当前出现次数的大小。如果堆顶更大,说明至少有k个数字的出现次数比当前值大,故舍弃当前值;否则,就弹出堆顶,并将当前值插入堆中
遍历完成后,堆中的元素就代表了【出现次数数组】中前k大的值。
class Solution {
public int[] topKFrequent(int[] nums, int k) {
HashMap<Integer, Integer> map = new HashMap<>();
int n = nums.length;
for (int i = 0; i < n; i++) {
map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
}
//int[]数组的第一个元素代表数组的值,第二个元素代表了该值出现的次数
PriorityQueue<int[]> queue = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
int num = entry.getKey();
int count = entry.getValue();
if (queue.size() < k) {
queue.add(new int[]{num, count});
} else {
if (queue.peek()[1] < count) {
queue.poll();
queue.add(new int[]{num, count});
}
}
}
int[] res = new int[k];
for (int i = 0; i < k; i++) {
res[i] = queue.poll()[0];
}
return res;
}
}
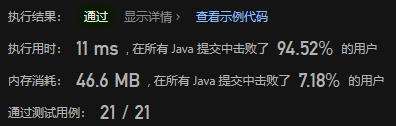
复杂度分析:
- 时间复杂度:O(Nlogk),其中N为数组的长度。首先遍历原数组,并使用哈希表记录出现次数,每个元素需要O(1)的时间,共需O(N)的时间。随后,遍历【出现次数数组】,由于堆大小至多为k,因此每次堆操作需要O(logk)的时间,共需O(Nlogk)的时间。二者之和为O(Nlogk)。
- 空间复杂度:O(N)。哈希表的大小为O(N),而堆的大小为O(k),共计为O(N)。