1. 十进制

1.1. 现代数学建立在十进制计数系统之上

2. 二进制

2.1. 二进制计数系统的工作原理与十进制计数系统一样，唯一的区别是前者的基数为2，而后者的基数为10

2.2. 数据压缩所做的就是尽可能减少表示特定数据集时所需的二进制位数量

2.3. 给定任意一个整数，我们都能将它转换为二进制形式

3. 十六进制

3.1. 用字母A来表示10，用B表示11，以此类推，用F表示15

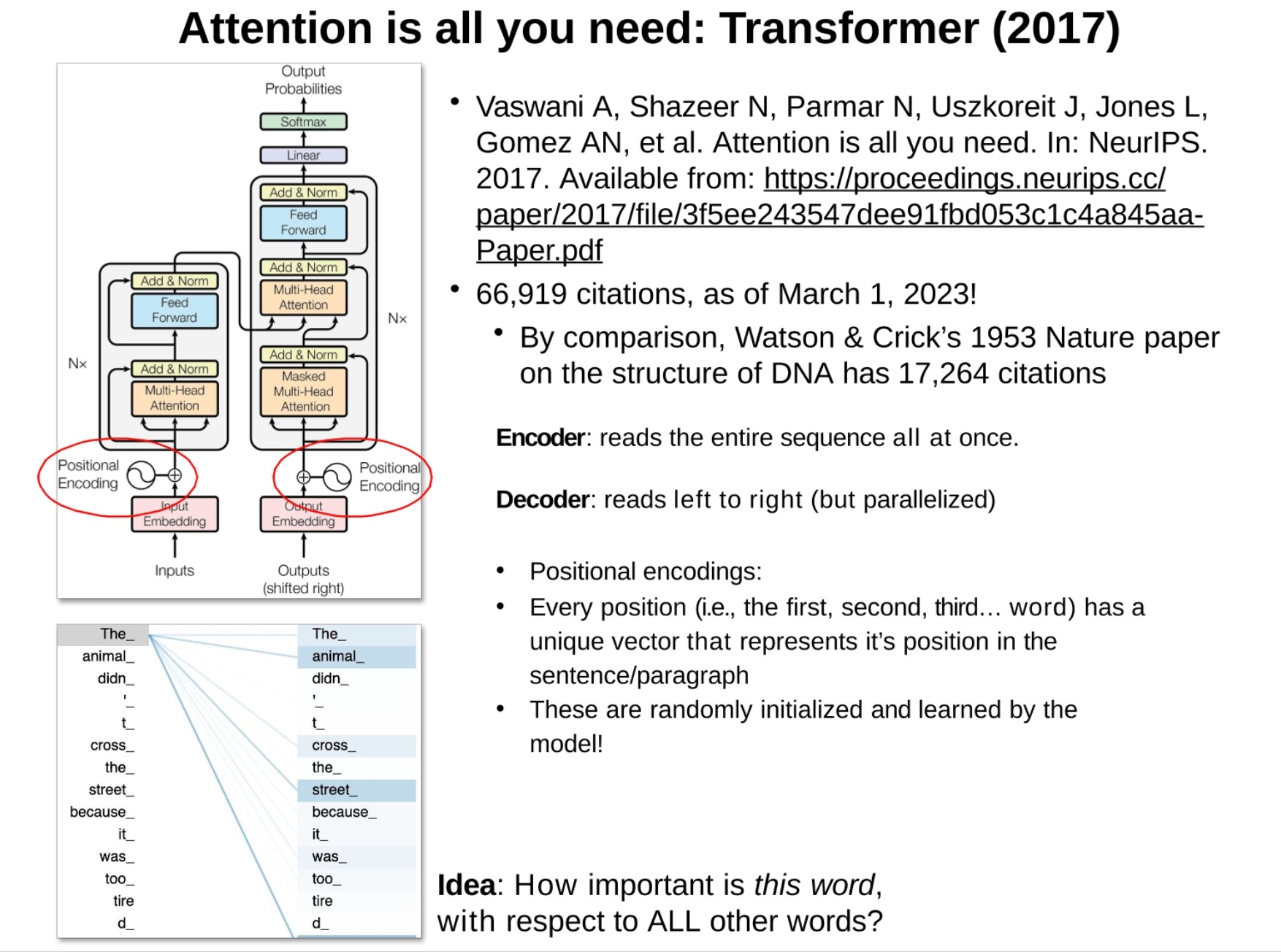
4. 信息论

4.1. 一个数值所包含的信息内容等于，为了在一个集合中唯一地确定这个数值，需要做出的二选一（是/否）决定的次数

5. 二分查找

5.1. 首先将数组中的数据集分成两半，然后判断要找的数值10比处于中间位置的枢轴值是大还是小

5.2. 如果一个数组包含偶数个元素，那么真正处于中间的元素是不存在的，可以根据喜好冲中间偏左或者偏右选择一个

6. 熵

6.1. 物理学中的解释

6.1.1. 一个热力学量，表示的是一个系统中无法转换为机械功的热能的量，通常被解释为该系统的无序度或随机度

6.2. 信息论中的解释

6.2.1. 对在特定的消息或语言中信息传输速度的一种对数度量

6.3. 表示一个数所需要的最少二进制位数

6.4. 一个数所需要的二进制位数lb(x)=(log(x)/log(2))

6.4.1. 二进制位已经是数据的最小单位，能使用的最小的二进制位数就是1

6.4.2. 必须对这个值向上取整，也就是使用向上取整函数，即ceil（或ceiling）函数

6.5. LOG2(x)=ceil(log(x+1)/log(2))

6.6. 一个集合的熵

6.6.1. H(S)=-∑pi×lb(pi)

6.7. 为了使表示某个数据集所需的二进制位数最少，数据集中的每个符号平均所需的最小二进制位数就是熵

6.8. 以一种倒排序的方式建立在数据流中每个符号出现概率的估算之上的

6.8.1. 一个符号出现得越频繁，它对整个数据集包含的信息内容的贡献就会越少

6.8.2. 很长的时间里没有什么有用的信息，真正有用的信息偶尔才会出现

7. 数据压缩算法的艺术

7.1. 真正试图去突破熵的限定

7.2. 将数据转换成一种熵值更小的、新的表现形式

8. 突破熵

8.1. 按照香农对熵的定义，他只考虑了符号出现的概率，完全没有考虑符号之间的排序

8.1.1. 对真实数据集来说，排序是一项基本的信息，符号之间的关系同样如此

8.2. 通过利用数据集的结构信息将其转换为一种新的表示形式，而这种新表示形式的熵比源信息的熵小

8.2.1. [Q,U,A,R,K] 和[K,R,U,Q,A] 这两个集合有相同的熵

8.2.2. [Q,U,A,R,K] 这个集合表示的是英语中一个有意义的单词

8.3. 增量编码（delta coding）

8.3.1. 如果相邻的值之间高度相关，那么用增量编码的方法可以转换数据，使其熵变得更小

8.3.2. 顺序很重要

8.4. 符号分组

8.4.1. 用单词作为符号，得到的熵值会更小

8.4.2. 如果数据集中存在连续值组合出现多次的情况，就可以利用这种情况来减小熵

8.4.3. 通过最佳符号分组预处理数据，会得到一个较小的熵值

8.5. 排列

8.5.1. 一个排列就是原来的集合打乱顺序后的一个版本

8.5.2. 对数直接进行编码时，共需要24个二进制位，而对下标编码时，只需要18个二进制位，也就是节省了大约25% 的空间

9. 标准的数字长度

9.1. 用最少的二进制位数来表示一个数，在解码相应的二进制字符串时会产生混乱（因为我们并不知道该数对应的LOG2长度），会与硬件的执行性能相冲突，两者不能兼顾

9.2. 折中的方案

9.2.1. 用固定长度的二进制位数来表示大小不同的整数

9.2.2. 最基本的存储单元是一个字节，由8个二进制位组成

9.3. 信息论与实际实现层面的差别

9.3.1. 绝大多数算法使用预先设定好的固定的二进制位长度，而不是通过LOG2函数计算出的二进制位长度

10. 柯尔莫哥洛夫复杂性

10.1. Kolmogorov complexity

10.2. 以数学家安德雷•柯尔莫哥洛夫（Andrey Kolmogorov）的名字命名，以纪念他在1963年发表了这方面的第一篇论文

10.3. 度量的是确定一个对象所需要的计算资源

10.3.1. 为了准确地生成数据，所需要的生成程序的大小

10.4. 任何字符串的柯尔莫哥洛夫复杂性顶多比字符串本身的长度大几个字节(基本上，也就是一个程序输出字符串的每个元素）

10.5. 逻辑综合（logic synthesis）或者程序综合（program synthesis）进行数据压缩的时候，柯尔莫哥洛夫复杂性就开始真正起作用了

10.5.1. 本质上它取的是数据集以及反向生成产生字符串的程序的二进制位流