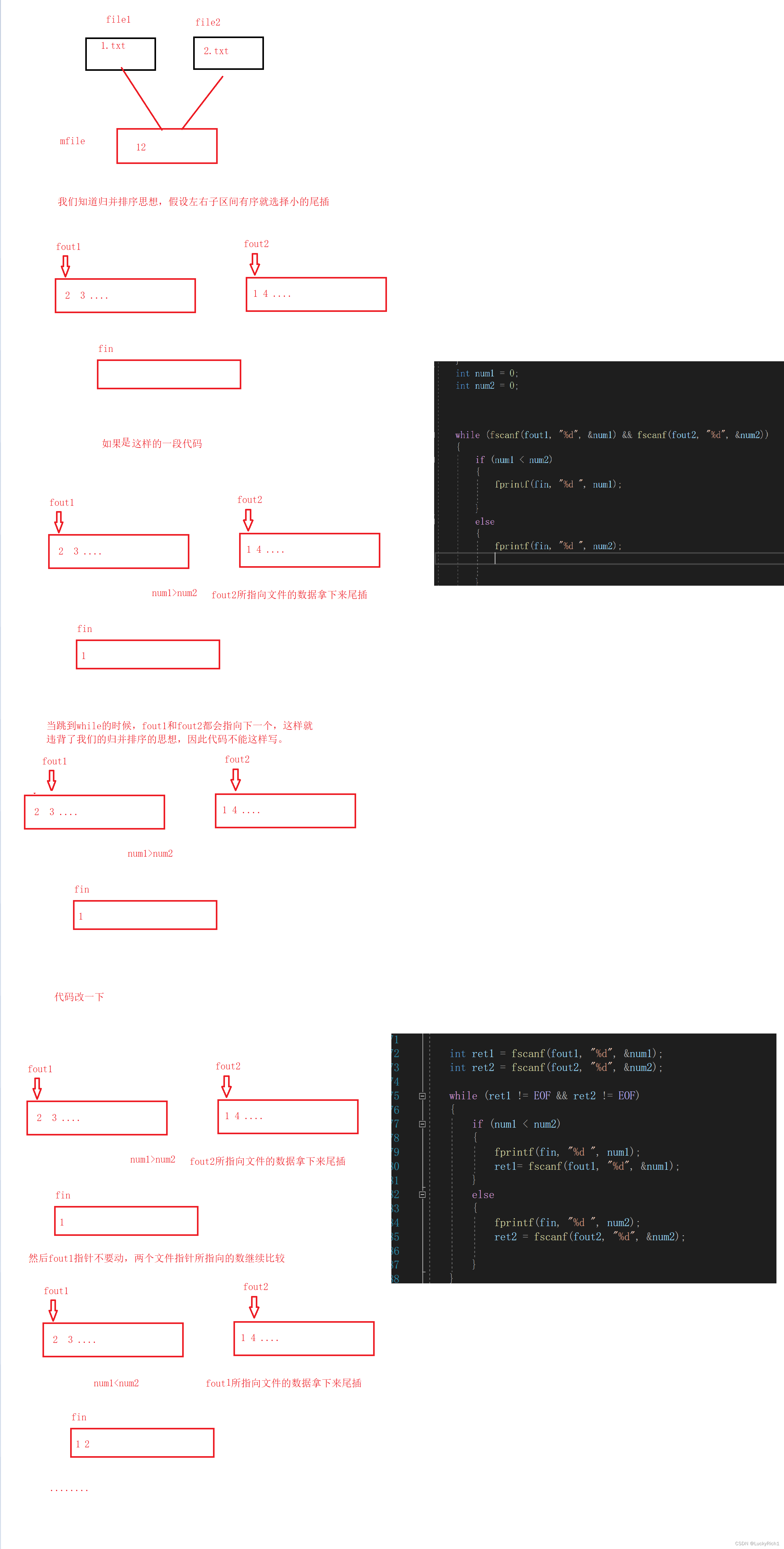
题目:HJ10 字符个数统计
牛客网上一道简单的题目,计算字符串中含有的不同字符的个数,一看这个题目,通常直接意识到方案的基本实现思路:设置一个容器,遍历字符串中的每个字符,若字符与容器中字符相同,则不添加,否则加入,最后统计容器字符的个数;
Java语言开发,很容易想到通过Set容器剔除,所以有下列的实现
方案一:通过SET剔除重复实现
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String line = in.nextLine();
Set<Character> set = new HashSet<>(128);
char[] chars = line.toCharArray();
for (int i = 0; i < chars.length; i++) {
set.add(chars[i]);
}
System.out.println(set.size());
}
}
}
通过set方案实现了,而且结果显示也通过了。但如果只是到这里一步,还远远不够,至少还要分析时间复杂度和空间复杂度,判断是否有更优方案
1. 时间复杂度分析
代码外层使用了一次for循环遍历数组,时间复杂度O(N),
内层set.add方法底层使用Map的putVal
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
Map结果在jdk8中采用数组+链表+红黑树结构存储,在putVal时判断tab[i = (n - 1) & hash]是否为null,可以简单理解就是计算valued的hashcode,并通过hashcode值算出在数组的索引位置,看这个索引位置是否有值,若有值,则继续判断value是否相等,若相等则不添加,这个过程是O(1),但若不相等,则会在链化或者树化,链表插入时间复杂度O(1),树插入平均时间复杂度为O(LogN),由于链表超过8个节点后会树化,所以时间复杂度平均为O(LogN)
2. 空间复杂度分析
预估容量O(N),若一个字符是1k,10个字符就是10k。
从上诉两方面分析,SET方案时间复杂度外层循环避免不了,内层中map.putval优化已经非常极致了,空间复杂度是O(N)。一般Set方案已经比较优秀了,但是奈何程序员的智慧是无穷尽的,我们回到问题本身我们只需要统计不重复数据的个数,并不需要知道容器中哪些字符,那容器中存放字符,再去判断数量,感觉有点浪费空间。所以我这里想到了位图方式,统计位图中1的位的数量即可。
方案二:通过Java的BitSet位图实现方案
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextLine()) {
String line = in.nextLine();
BitSet bitSet = new BitSet(128);
char[] chars = line.toCharArray();
for (int i = 0; i < chars.length; i++) {
if(!bitSet.get(chars[i])){
bitSet.set(chars[i]);
}
}
System.out.println(bitSet.cardinality());
}
}
}
BitSet源码分析
1. 构造函数分析
private final static int ADDRESS_BITS_PER_WORD = 6;
private long[] words;
public BitSet(int nbits) {
// nbits can't be negative; size 0 is OK
if (nbits < 0)
throw new NegativeArraySizeException("nbits < 0: " + nbits);
initWords(nbits);
sizeIsSticky = true;
}
private void initWords(int nbits) {
words = new long[wordIndex(nbits-1) + 1];
}
private static int wordIndex(int bitIndex) {
return bitIndex >> ADDRESS_BITS_PER_WORD;
}
首先确定bitSet中维护Long类型的words数组,words数组中每个索引位占ADDRESS_BITS_PER_WORD=6位,所以说若words数组数量为1,则可以存放1-63,若数组长度为2,能存放1-4095
上面在构造函数中指定了数据量128,通过initWords方法初始化words
数组的长度,让128-1=127右移6位,高6位补0,获取wordIndex为1
127的二进制->0111 1111
👉右移->6位,高6位补0
0[111 111]1->0[000 000]1
再将wordIndex+1=数组的长度,这样的做法将数据通过位存储,通过2个数组长度就能存储下128个数,大大减少了空间的存储量
2. Set方法和Get方法分析
//set方法
public void set(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
//获取数据所在数组索引位
int wordIndex = wordIndex(bitIndex);
//扩容
expandTo(wordIndex);
//通过或存储值
words[wordIndex] |= (1L << bitIndex); // Restores invariants
checkInvariants();
}
//get方法
public boolean get(int bitIndex) {
//不能为负值
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
//判断是否越界
checkInvariants();
//获取数据所在数组的索引位
int wordIndex = wordIndex(bitIndex);
//判断索引位置是否为0
return (wordIndex < wordsInUse)
&& ((words[wordIndex] & (1L << bitIndex)) != 0);
}
将get方法和set方法放到一起讲,这里有位运算设计比较巧妙的地方,
set方法中或运算保留word[wordIndex]中原位为1不变,是一个加运算,举例说明
若word[0]中原来存放了一个值2,即0000 0010,
现在word[0]中再放入4即0000 1000
4与2进行或运算
2->0000 0010
4->0000 1000
结果->0000 1010 等于6
现在word[0]=6
get方法中的与运算可以获取到原值,以上述word[0]=6来获取4举例
word[0]->0000 1010
4->0000 1000
与结果为-> 0000 1000 等于4
所以在set中存储words[wordIndex] |= (1L << bitIndex);
get判断是否有值是
return (wordIndex < wordsInUse)
&& ((words[wordIndex] & (1L << bitIndex)) != 0);
上面的wordsInUse变量赋值是在set方法的扩容方法中设置的,代表实际有值的数组长度
private void expandTo(int wordIndex) {
int wordsRequired = wordIndex+1;
if (wordsInUse < wordsRequired) {
ensureCapacity(wordsRequired);
wordsInUse = wordsRequired;
}
}
1.时间复杂度
代码外层使用了一次for循环遍历数组,时间复杂度O(N),
内层bitSet.set和get方法底层使用按位与运算(&)和按位或运算(|)的时间复杂度都是常数时间O(1),这是因为它们是在位级别上进行操作,每一位的操作可以在常数时间内完成。
无论操作数的位数多少,按位与运算和按位或运算都只需对每一对对应位进行逻辑运算,不需要依次遍历每一位。这是因为在计算机内部,整数的位表示是以二进制形式存储的,并且在硬件电路层面上,按位与运算和按位或运算可以同时对所有位进行并行操作。
2.空间复杂度
参考博文:两种工具查询Java嵌套对象引用内存大小
public static void main(String[] args) {
StringBuffer sb = new StringBuffer();
sb.append("abcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyz");
Set<Character> set = new HashSet<>(128);
BitSet bitSet = new BitSet(128);
char[] chars = sb.toString().toCharArray();
for (int i = 0; i < chars.length; i++) {
set.add(chars[i]);
if (!bitSet.get(chars[i])) {
bitSet.set(chars[i]);
}
}
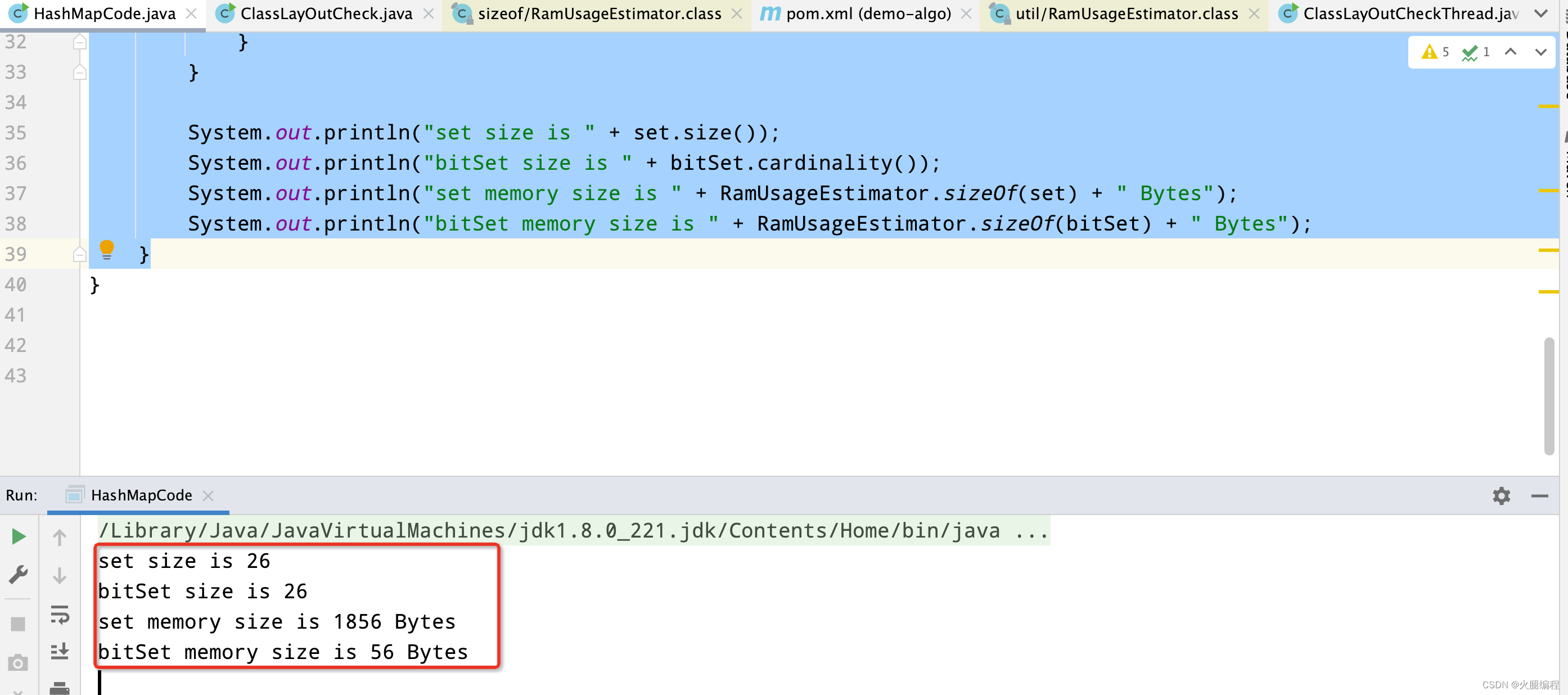
System.out.println("set size is " + set.size());
System.out.println("bitSet size is " + bitSet.cardinality());
System.out.println("set memory size is " + RamUsageEstimator.sizeOf(set) + " Bytes");
System.out.println("bitSet memory size is " + RamUsageEstimator.sizeOf(bitSet) + " Bytes");
}
对于同一个字符串中,bitset占用空间明显比set占用空间要小很多
总结
看来每个问题都不只有一种解法,每一种解法优缺点分析需要理解底层的逻辑,并借助工具去呈现最终的结果,只要我们想到并且动手实践,也许也没有那么难



![[论文阅读73]Prefix-Tuning:Optimizing Continuous Prompts for Generation](https://img-blog.csdnimg.cn/img_convert/77966bd7d1736d534e56a1d727de19f5.png)