Python中求最大公约数的方法及实现
在数学中,最大公约数是指两个或多个整数的共同约数中最大的一个。对于Python开发工程师来说,求最大公约数是一个非常基本的操作,尤其在处理算法或数学题目时更加常见。本篇文章就是为了帮助大家更好的理解Python中的求最大公约数的方法及实现。
欧几里得算法
欧几里得算法,也称作辗转相减法,是从古希腊开始使用的一种求最大公约数的算法。它构造了一种始终得到计算终止的方法。
原理
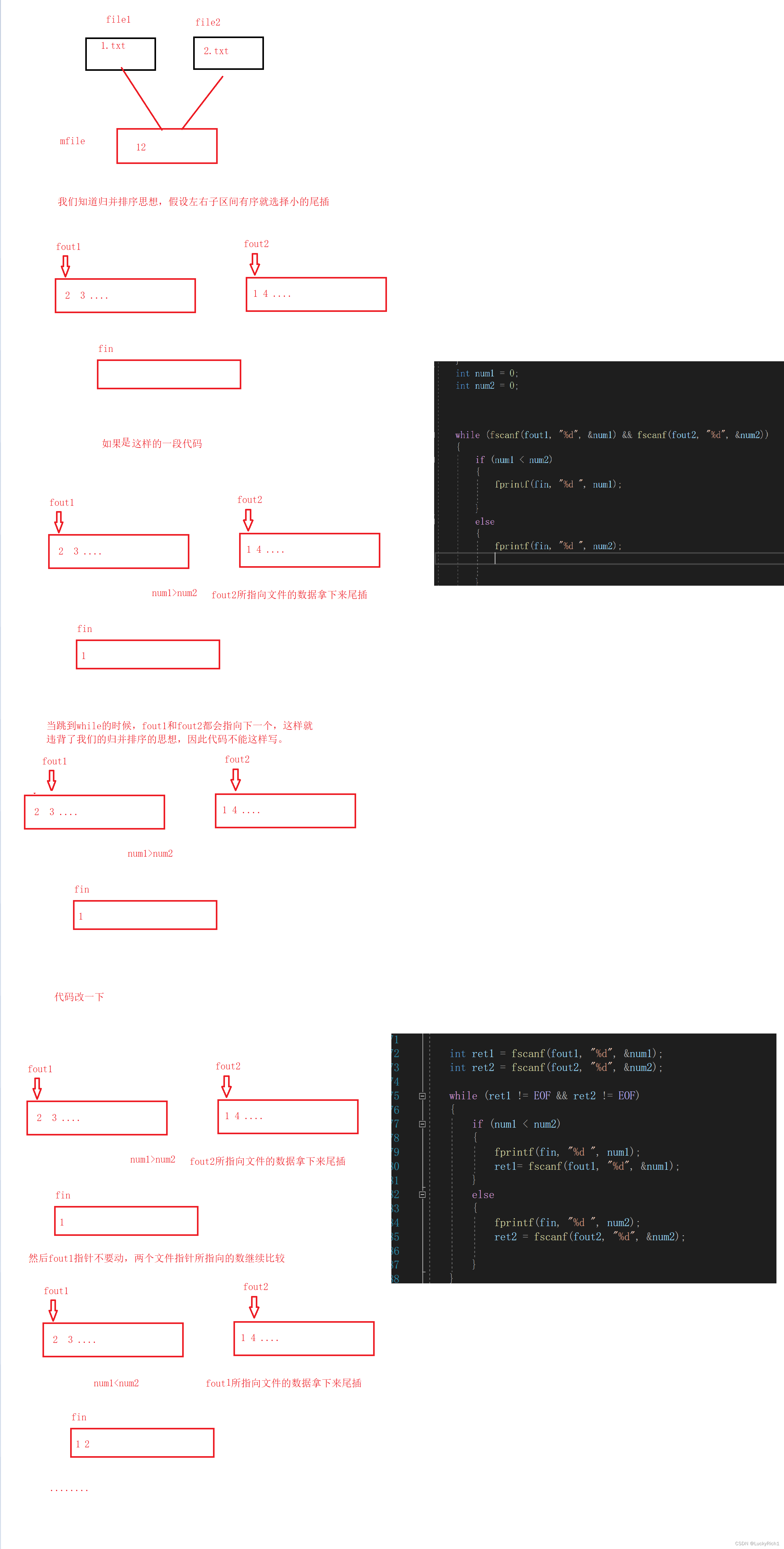
设a,b是两个正整数,且a>b,a=kb+r(0<=r<b),那么:gcd(a,b)=gcd(b,r) (k为a与b的最大公约数)由于r=a-kb,因此gcd(a,b)=gcd(b,a-kb),又因为若d|a,d|b则有d|a-kb,r|a-bk,即r|gcd(a,b),因此gcd(a,b)=gcd(b,a mod b),得到辗转相除法的基本性质。
代码实现
下面是一个简单的Python函数来实现欧几里得算法:
def gcd_Euclid(a,b):
while(b):
a,b = b,a%b
return a
在这行代码中,我们使用了while循环来进行求解,不断地用大数对小数取模,直到取模后的结果为0,此时较小的数就是最大公约数。
更相减损术
更相减损术,又称减法求最大公约数法,适用于两个大整数排序相近的情况,因为每次递归的两个数都不会太大,递归深度最小,适用于两数相差不大且都是偶数的情况。
原理
设a,b是两个正整数,若a<b,则a,b互换。然后a=a-b,g=gcd(a,b),再用a与g比较,若a>g,则a,g互换。因为b,a mod b的差可能很大,甚至可能变为原数的2倍、3倍等,应该使用更为平均的减法(例如,每次减去一个较小的值)。
代码实现
下面是一个简单的Python函数来实现更相减损术:
def gcd_Subtraction(a,b):
if a < b:
a,b = b,a
if a == b:
return a
else:
return gcd_Subtraction(a-b, b)
在这个代码行中,我们使用了递归来进行求解,如果a小于b,我们交换它们的位置。如果a等于b,我们就返回a。否则,我们递归调用此函数,一直做减法操作,直到a等于b,这样我们就得到了最大公约数。
结论
以上就是Python中求最大公约数的两种算法及代码实现。欧几里得算法适用于处理两个较大的整数,而更相减损术适用于两个数排序接近的情况,如果您需要计算更多的最大公约数,您可以使用这两种算法。无论您使用哪种方法,都应该注意一个大数对计算性能的影响。保持良好的算法习惯是编写高效Python代码的关键,因此我们建议您在编写代码时选择最佳算法,并学习如何优化您的代码以提高性能。
最后的最后
本文由chatgpt生成,文章没有在chatgpt生成的基础上进行任何的修改。以上只是chatgpt能力的冰山一角。作为通用的Aigc大模型,只是展现它原本的实力。
对于颠覆工作方式的ChatGPT,应该选择拥抱而不是抗拒,未来属于“会用”AI的人。
🧡AI职场汇报智能办公文案写作效率提升教程 🧡 专注于AI+职场+办公方向。
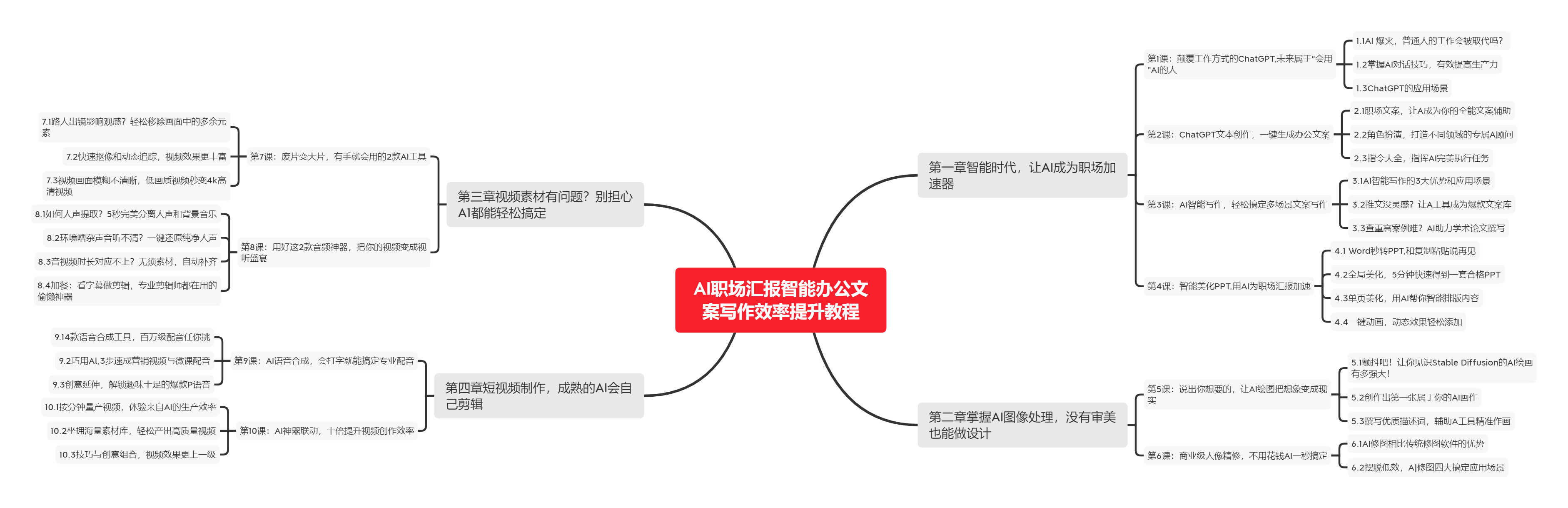
下图是课程的整体大纲

下图是AI职场汇报智能办公文案写作效率提升教程中用到的ai工具

🚀 优质教程分享 🚀
- 🎄可以学习更多的关于人工只能/Python的相关内容哦!直接点击下面颜色字体就可以跳转啦!
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| 🧡 AI职场汇报智能办公文案写作效率提升教程 🧡 | 进阶级 | 本课程是AI+职场+办公的完美结合,通过ChatGPT文本创作,一键生成办公文案,结合AI智能写作,轻松搞定多场景文案写作。智能美化PPT,用AI为职场汇报加速。AI神器联动,十倍提升视频创作效率 |
| 💛Python量化交易实战 💛 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
| 🧡 Python实战微信订餐小程序 🧡 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |


![[论文阅读73]Prefix-Tuning:Optimizing Continuous Prompts for Generation](https://img-blog.csdnimg.cn/img_convert/77966bd7d1736d534e56a1d727de19f5.png)