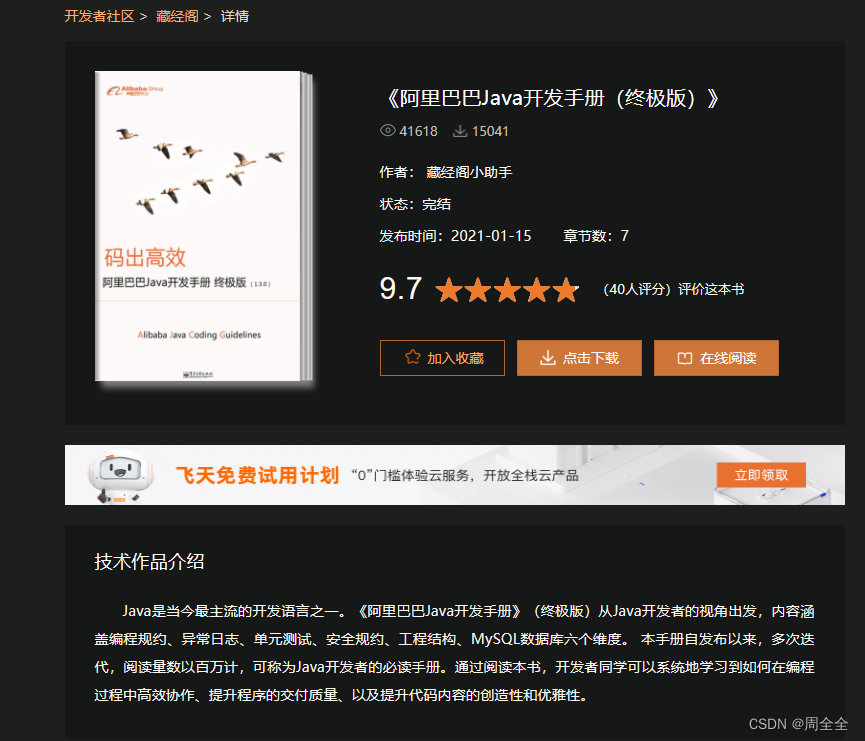
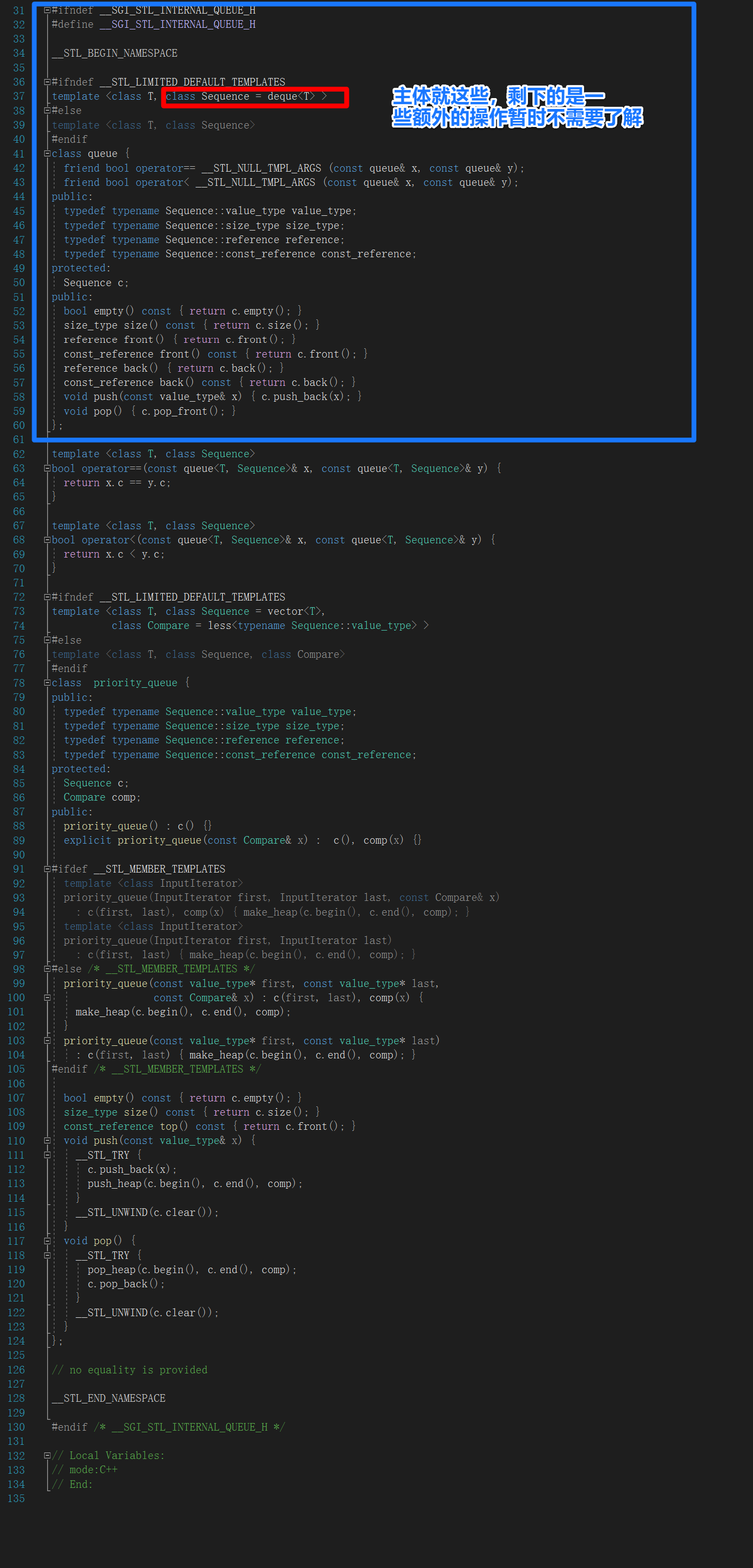
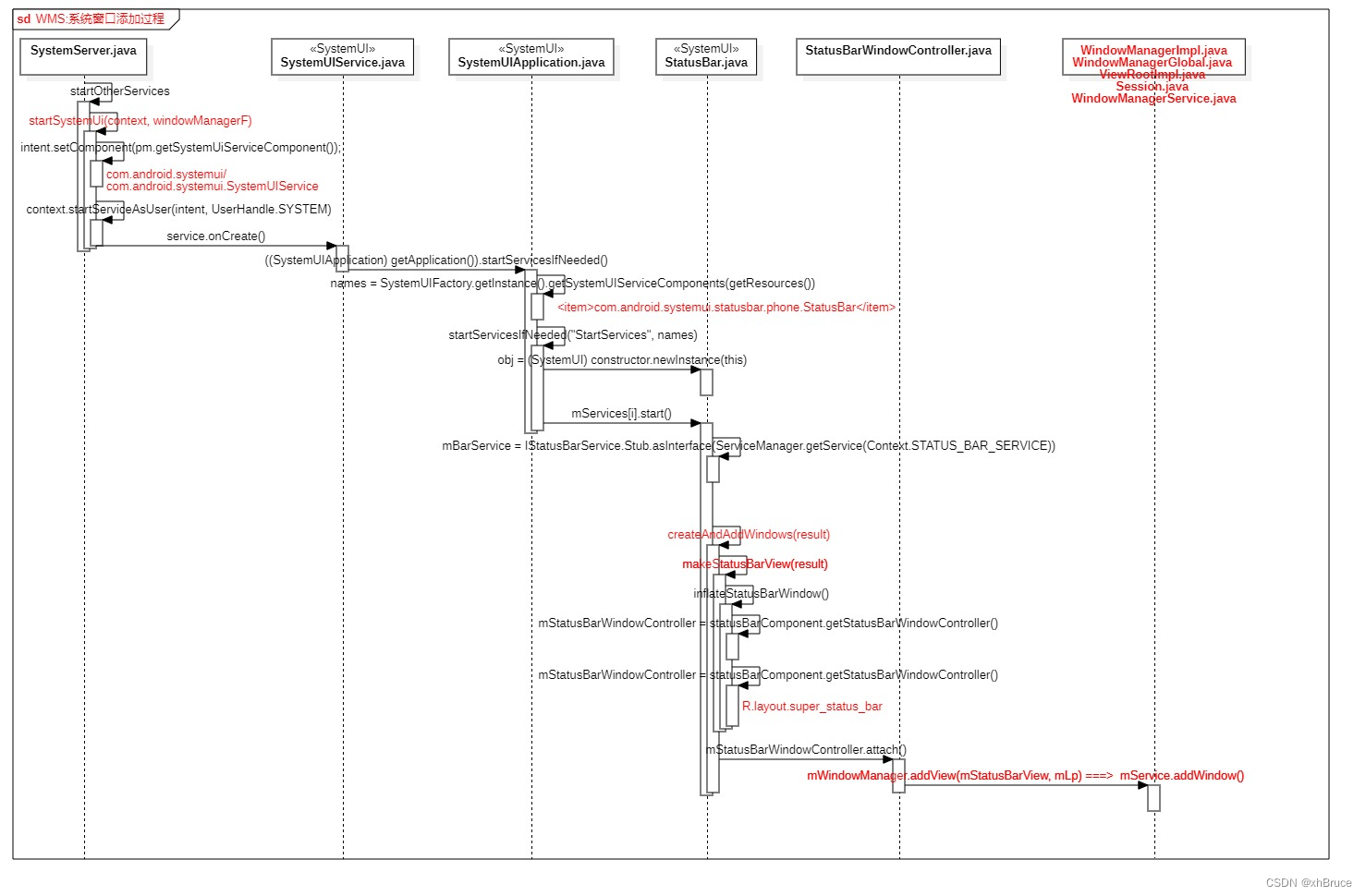
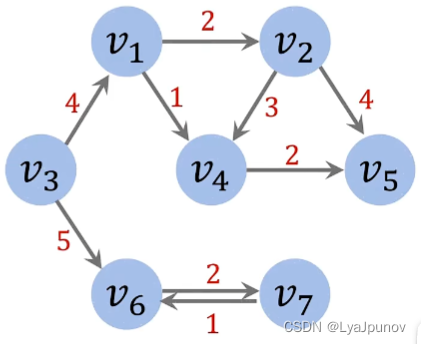
图的基本概念

无向图

边是没有方向的，也就是双向的

结点 V = { v 1 , v 2 , . . . , v 7 } \mathcal{V} = \{ v_1,v_2,...,v_7\} V={v1​,v2​,...,v7​}

边 ε = { e 1 , 2 , e 1 , 3 , . . . , e 6 , 7 } \varepsilon = \{e_{1,2},e_{1,3},...,e_{6,7}\} ε={e1,2​,e1,3​,...,e6,7​}

图 G = { V , ε } \mathcal{G} = \{ \mathcal{V},\varepsilon \} G={V,ε}

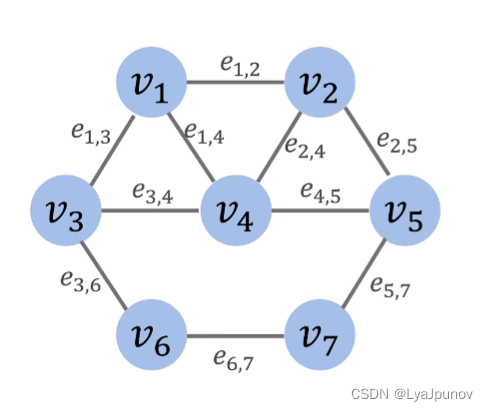
有向图

边是有方向的，也就是单向的

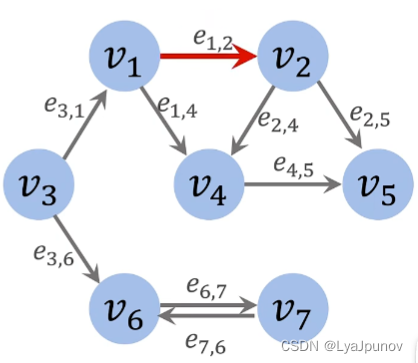
无权图

边没有权重，也可以理解为权重都是1

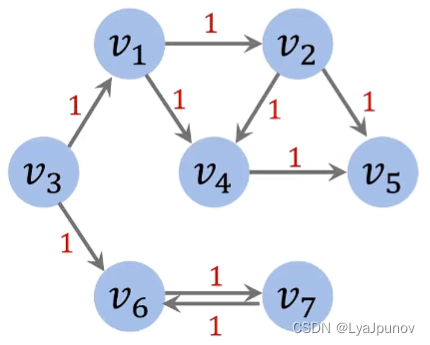
有权图

边有权重

图的数据结构

邻接矩阵与邻接表

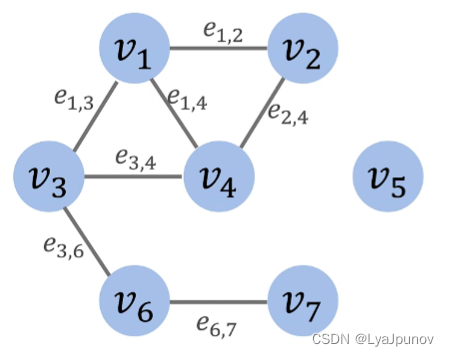
无向无权图

邻接表(Adjacency list)

表示结点与谁相连，

vertex	Neighbors
1	2,3,4
2	1,4
3	1,4,6
4	1,2,3
5	empty
6	3,7
7	6

领接矩阵(Adjacency matrix)

$$\left[\begin{array}{ccccccc}0& 1& 1& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 1& 0\\ 1& 1& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right]$$

邻接矩阵表示结点 $i$ 和结点 $j$ 之间的权重，如果是无权图，权重就是1。无向图的邻接矩阵都是对称的。因为边是双向的。

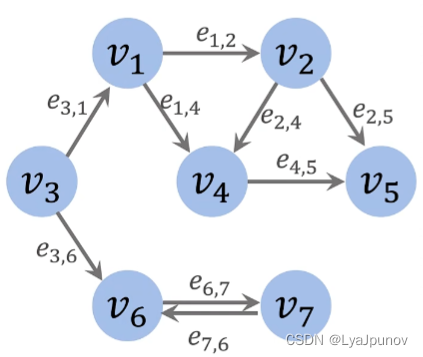
有向无权图

邻接表(Adjacency list)

表示结点与谁相连，

vertex	Neighbors
1	2,4
2	4,5
3	1,6
4	5
5	empty
6	7
7	6

领接矩阵(Adjacency matrix)

$$\left[\begin{array}{ccccccc}0& 1& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 0& 0\\ 1& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right]$$

邻接矩阵表示结点 $i$ 和结点 $j$ 之间的权重。列表示出发的点，行表示达到的点，比如 $a_{1,2}=1$ 表示从结点1到结点2 有一条单向的边。

有权图

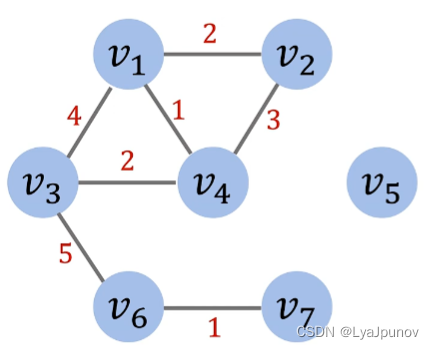
邻接矩阵(Adjacency matrix)

$$\left[\begin{array}{ccccccc}0& 2& 4& 1& 0& 0& 0\\ 2& 0& 0& 3& 0& 0& 0\\ 4& 0& 2& 0& 0& 5& 0\\ 1& 3& 2& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 5& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right]$$

其实和无向图很像，就是表示两个结点之间的链接，有权图有权重，无权图没有

度矩阵(degree matrix)

度矩阵是图论中一个重要的概念，用于描述无向图或有向图中每个节点的度数。它是一个对角矩阵，矩阵中的元素 $d_i$ 表示节点 $i$ 的度数，即与节点 $i$ 相连的边的数量。

无向图

上图的度矩阵为
$$\left[\begin{array}{ccccccc}3& 0& 0& 0& 0& 0& 0\\ 0& 2& 0& 0& 0& 0& 0\\ 0& 0& 3& 0& 0& 0& 0\\ 0& 0& 0& 3& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 2& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right]$$
可见，是一个对角矩阵。

有向图

对于有向图而言，可以分为出度矩阵和入度矩阵。出度矩阵代表每个节点的出度，入度矩阵代表每个节点的入度。这个就很好计算了，不在演示

拉普拉斯矩阵(Laplacian matrix)

拉普拉斯矩阵用来表述图的性质，关于拉普拉斯矩阵的计算一般有如下几种方法

1、Symmetric normalized Laplacian：设 L 为图 G 的拉普拉斯矩阵，D 是度数矩阵，则对称归一化拉普拉斯矩阵为$L_{sym}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}$。

2、Random walk Laplacian：设 $M=D^{-1}L$，则随机游走拉普拉斯矩阵为 $L_{rwl}=I-M$，其中 $I$ 是单位矩阵。

3、Unnormalized Laplacian：不进行归一化的拉普拉斯矩阵可以表示为 $L=D-A$，其中A为邻接矩阵，D为度矩阵

矩阵性质[1]

• 0是他的特征值，$1_N$ 为特征向量

• $x^T\ell x=\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{a}_{ij}(x_j-x_i{)}^2$ ，$\ell$ 的半正定性意味着 $\ell$ 的所有特征根都是实数且非负

• 如果G是连通的，那么 $\ell$ 的第二小的特征根，可以用 ${\lambda }_2(\ell )$ ，称为G的代数连通性，其大于0

• G的代数连通性等于 $mi{n}_{x\ne 0,1_N^{T}x=0}\frac{x^T\ell x}{x^{T}x}$，因此，如果 $1_N^T x = 0,x^T \ell x \ge \lambda_2(\ell)x^Tx $ 。

参考文献

[1] R. Olfati-Saber, R.M. Murray, Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 49(9), 1520–1533 (2004)

文中的图来自王树森大佬的课程，课程并未细看，只需要这些基础知识。