从上次写文章到现在已经27天了,将近一个月蒟蒻没有更新了。
最近学的ST表太难理解了,再加上忙,一直没时间……
---------------------------------------------------------------------------------------------------------------------------------
开始之前,请各位(尤其蒟蒻,大佬绕开这里)做好心理准备,有可能你真的会看1~2遍才能懂,因为本蒟蒻就是这样……
正文开始
今天我们所讲的叫做ST表,也被称为倍增表。
ST表一般来说是用来处理“区间最值问题”(RMQ问题),就比如一个区间内的最大值、最小值之类的。
一提到区间最值问题,第一反应肯定会想到直接for循环枚举,但这种时间复杂度实在高,如果有m次询问,那么时间就得达到大约O(mn) (蒟蒻算时间复杂度很垃圾,也许不对:( ),但使用ST表,时间就会骤降到O(nlogn),其中,每次询问只是O(1)的时间,太猛了简直。
思想:
ST表采用动态规划的思想,但是他表达状态的方式不太一样。(不要问发明的人怎么想到的,记就完了)
我们先假设求区间最大值
定义f[i][j]表示从i开始,向后2^j个数这个区间内的最大值。那么我们看下图:

注:个数为(尾-头+1),所以i+2^j-1-i+1=2^j
上图为整体,我们把这个整体分成两部分
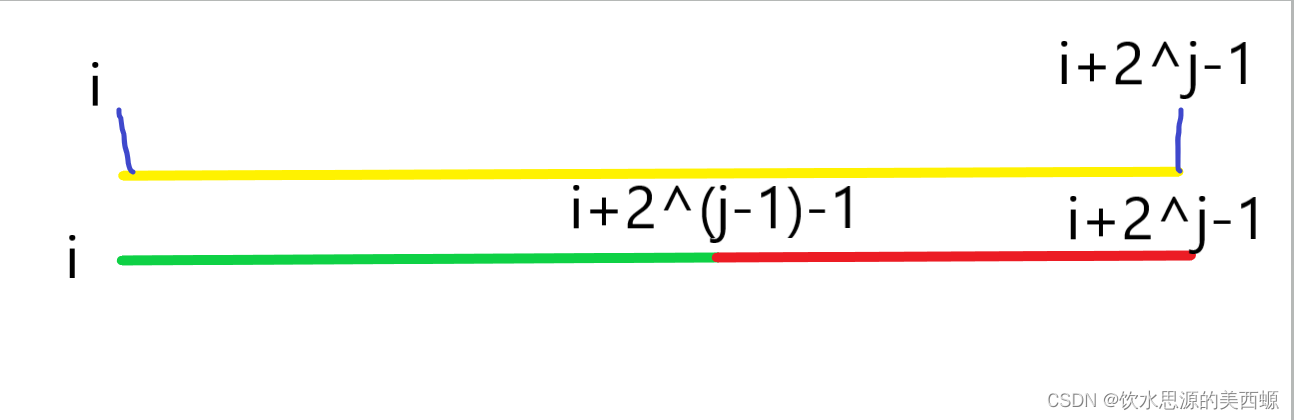
我们既然分为两个部分了,那么我们最后的那个结果,不管绿的部分的右端点在哪儿,或者红部分的左端点在哪儿,我们的结果都不发生改变。所以要极端一点:假设以下部分:
i+2^j-1=r(其中r为我们所求全部区间的右端点)
r-2^j+1=l(l为我们所求全部区间的左端点)
最后求出来,j=log2(r-l+1) 请没学过log的同学自行补习,比如本蒟蒻:(((
那么整个区间的最大值,就是两部分最大值再次进行比较。
得出状态转移方程:
f[i][j]=max(f[i][j-1],f[i+2^(j-1)][j-1])
思路差不多就讲完了,下面来看看模板代码:
在难懂的地方我会有注释,实在不懂私信蒟蒻()
scanf("%lld%lld",&n,&m);
for (int i=1;i<=n;i++){
scanf("%lld",&f[i][0]);
}
for (int j=1;(1<<j)<=n;j++){//枚举那个指数,运用位运算
for (int i=1;i<=n-(1<<j)+1;i++){//枚举所有剩下的i的情况
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);//转移方程,里面还是使用位运算,因为一个字,快
}
}
for (int i=1;i<=m;i++){
int l,r;
scanf("%lld%lld",&l,&r);
int s=log2(r-l+1);//反求一下指数
printf("%lld\n",max(f[l][s],f[r-(1<<s)+1][s]));//两个区间取最大值
}例题:
纯纯大模板
给定一个长度为 N 的数列,和 M 次询问,求出每一次询问的区间内数字的最大值。
输入
第一行包含两个整数 N,M,分别表示数列的长度和询问的个数。
第二行包含 N 个整数(记为 ai),依次表示数列的第 i 项。
接下来 M 行,每行包含两个整数 li,ri,表示查询的区间为 [li,ri]。
输出
输出包含 M 行,每行一个整数,依次表示每一次询问的结果。
样例输入1
8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8
样例输出1
9
9
7
7
9
8
7
9希望各位同学在自己理解的基础上,尽量独立完成
分析优缺点:
优点:时间太猛辣!空间太猛辣!
缺点:不能修改任何的值,除非使用线段树
今天对于ST表的讲解就到这里,大家下期再见!