文章目录
- 周赛347
- [2710. 移除字符串中的尾随零](https://leetcode.cn/problems/remove-trailing-zeros-from-a-string/)
- 模拟
- [2711. 对角线上不同值的数量差](https://leetcode.cn/problems/difference-of-number-of-distinct-values-on-diagonals/)
- 模拟
- [2712. 使所有字符相等的最小成本](https://leetcode.cn/problems/minimum-cost-to-make-all-characters-equal/)
- 结论题(思维题)
- [2713. 矩阵中严格递增的单元格数](https://leetcode.cn/problems/maximum-strictly-increasing-cells-in-a-matrix/)
- 动态规划 + 优化(如何思考?)
周赛347
2710. 移除字符串中的尾随零
难度简单1
给你一个用字符串表示的正整数 num ,请你以字符串形式返回不含尾随零的整数 num 。
示例 1:
输入:num = "51230100"
输出:"512301"
解释:整数 "51230100" 有 2 个尾随零,移除并返回整数 "512301" 。
示例 2:
输入:num = "123"
输出:"123"
解释:整数 "123" 不含尾随零,返回整数 "123" 。
提示:
1 <= num.length <= 1000num仅由数字0到9组成num不含前导零
模拟
class Solution {
public String removeTrailingZeros(String num) {
int j = num.length() - 1;
while(j >= 0 && num.charAt(j) - '0' == 0)
j -= 1;
return num.substring(0, j+1);
}
}
2711. 对角线上不同值的数量差
难度中等4
给你一个下标从 0 开始、大小为 m x n 的二维矩阵 grid ,请你求解大小同样为 m x n 的答案矩阵 answer 。
矩阵 answer 中每个单元格 (r, c) 的值可以按下述方式进行计算:
- 令
topLeft[r][c]为矩阵grid中单元格(r, c)左上角对角线上 不同值 的数量。 - 令
bottomRight[r][c]为矩阵grid中单元格(r, c)右下角对角线上 不同值 的数量。
然后 answer[r][c] = |topLeft[r][c] - bottomRight[r][c]| 。
返回矩阵 answer 。
矩阵对角线 是从最顶行或最左列的某个单元格开始,向右下方向走到矩阵末尾的对角线。
如果单元格 (r1, c1) 和单元格 (r, c) 属于同一条对角线且 r1 < r ,则单元格 (r1, c1) 属于单元格 (r, c) 的左上对角线。类似地,可以定义右下对角线。
示例 1:

输入:grid = [[1,2,3],[3,1,5],[3,2,1]]
输出:[[1,1,0],[1,0,1],[0,1,1]]
解释:第 1 个图表示最初的矩阵 grid 。
第 2 个图表示对单元格 (0,0) 计算,其中蓝色单元格是位于右下对角线的单元格。
第 3 个图表示对单元格 (1,2) 计算,其中红色单元格是位于左上对角线的单元格。
第 4 个图表示对单元格 (1,1) 计算,其中蓝色单元格是位于右下对角线的单元格,红色单元格是位于左上对角线的单元格。
- 单元格 (0,0) 的右下对角线包含 [1,1] ,而左上对角线包含 [] 。对应答案是 |1 - 0| = 1 。
- 单元格 (1,2) 的右下对角线包含 [] ,而左上对角线包含 [2] 。对应答案是 |0 - 1| = 1 。
- 单元格 (1,1) 的右下对角线包含 [1] ,而左上对角线包含 [1] 。对应答案是 |1 - 1| = 0 。
其他单元格的对应答案也可以按照这样的流程进行计算。
示例 2:
输入:grid = [[1]]
输出:[[0]]
解释:- 单元格 (0,0) 的右下对角线包含 [] ,左上对角线包含 [] 。对应答案是 |0 - 0| = 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n, grid[i][j] <= 50
模拟
class Solution {
public int[][] differenceOfDistinctValues(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] res = new int[m][n];
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
Set<Integer> topleft = new HashSet<>();
Set<Integer> bottomright = new HashSet<>();
int k = i-1, x = j-1;
while(k >= 0 && x >= 0){
topleft.add(grid[k][x]);
k -= 1;
x -= 1;
}
k = i+1; x = j+1;
while(k < m && x < n){
bottomright.add(grid[k][x]);
k += 1;
x += 1;
}
res[i][j] = Math.abs(topleft.size() - bottomright.size());
}
}
return res;
}
}
2712. 使所有字符相等的最小成本
难度中等6
给你一个下标从 0 开始、长度为 n 的二进制字符串 s ,你可以对其执行两种操作:
- 选中一个下标
i并且反转从下标0到下标i(包括下标0和下标i)的所有字符,成本为i + 1。 - 选中一个下标
i并且反转从下标i到下标n - 1(包括下标i和下标n - 1)的所有字符,成本为n - i。
返回使字符串内所有字符 相等 需要的 最小成本 。
反转 字符意味着:如果原来的值是 ‘0’ ,则反转后值变为 ‘1’ ,反之亦然。
示例 1:
输入:s = "0011"
输出:2
解释:执行第二种操作,选中下标 i = 2 ,可以得到 s = "0000" ,成本为 2 。可以证明 2 是使所有字符相等的最小成本。
示例 2:
输入:s = "010101"
输出:9
解释:执行第一种操作,选中下标 i = 2 ,可以得到 s = "101101" ,成本为 3 。
执行第一种操作,选中下标 i = 1 ,可以得到 s = "011101" ,成本为 2 。
执行第一种操作,选中下标 i = 0 ,可以得到 s = "111101" ,成本为 1 。
执行第二种操作,选中下标 i = 4 ,可以得到 s = "111110" ,成本为 2 。
执行第一种操作,选中下标 i = 5 ,可以得到 s = "111111" ,成本为 1 。
使所有字符相等的总成本等于 9 。可以证明 9 是使所有字符相等的最小成本。
提示:
1 <= s.length == n <= 105s[i]为'0'或'1'
结论题(思维题)
https://leetcode.cn/problems/minimum-cost-to-make-all-characters-equal/solution/yi-ci-bian-li-jian-ji-xie-fa-pythonjavac-aut0/
class Solution:
def minimumCost(self, s: str) -> int:
# 结论1 : 先选择下标1反转再反转下标2 和 先反转下标2再反转下标1 结果相同
# ==> 可以从左到右反转
# 结论2 : 当s[i-1] != s[i]时,必须反转,
# 而操作:反转左边和反转右边 对[i+1:n]对答案的结果 影响相同
# 或者说 反转前不同的,反转后仍然不同
# ==> 当s[i-1] != s[i]时,反转成本少的
n = len(s)
ans = 0
for i in range(1, n):
if s[i-1] != s[i]:
ans += min(i, n-i)
return ans
2713. 矩阵中严格递增的单元格数
难度困难16
给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值 严格大于 当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
示例 1:
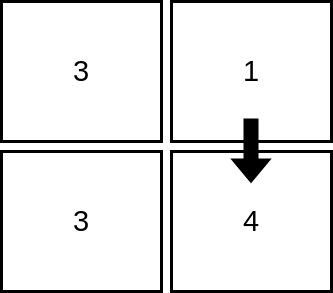
输入:mat = [[3,1],[3,4]]
输出:2
解释:上图展示了从第 1 行、第 2 列的单元格开始,可以访问 2 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 2 个单元格,因此答案是 2 。
示例 2:
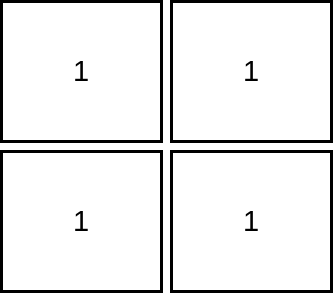
输入:mat = [[1,1],[1,1]]
输出:1
解释:由于目标单元格必须严格大于当前单元格,在本示例中只能访问 1 个单元格。
示例 3:
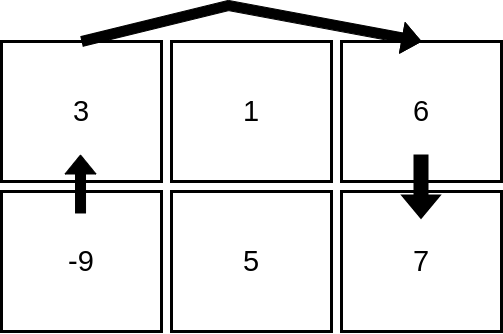
输入:mat = [[3,1,6],[-9,5,7]]
输出:4
解释:上图展示了从第 2 行、第 1 列的单元格开始,可以访问 4 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 4 个单元格,因此答案是 4 。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1051 <= m * n <= 105-105 <= mat[i][j] <= 105
动态规划 + 优化(如何思考?)
https://leetcode.cn/problems/maximum-strictly-increasing-cells-in-a-matrix/solution/dong-tai-gui-hua-you-hua-pythonjavacgo-b-axv0/
class Solution {
/**
直接DP超时
定义 f[i][j] 表示到达 mat[i][j] 时所访问的单元格的最大数量。那么答案就是所有 f[i][j] 的最大值。
考虑转移来源,不需要知道具体从哪个单元格转移过来,只需要知道转移来源的最大值时多少
维护每一行的 f[i][j] 的最大值
维护每一列的 f[i][j] 的最大值
按照元素值的顺序从小到大计算
*/
public int maxIncreasingCells(int[][] mat) {
var g = new TreeMap<Integer, List<int[]>>();
int m = mat.length, n = mat[0].length;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
// 相同元素放在同一组,统计位置
g.computeIfAbsent(mat[i][j], k -> new ArrayList<>()).add(new int[]{i, j});
int ans = 0;
int[] rowMax = new int[m], colMax = new int[n];
for (var pos : g.values()) { // 按照元素值从小到大进行遍历,顺序与矩阵每行每列的顺序无关
var mx = new int[pos.size()]; // 先把最大值算出来,再更新 rowMax 和 colMax
for (int i = 0; i < pos.size(); i++) {
mx[i] = Math.max(rowMax[pos.get(i)[0]], colMax[pos.get(i)[1]]) + 1;
ans = Math.max(ans, mx[i]);
}
for (int k = 0; k < pos.size(); k++) {
int i = pos.get(k)[0], j = pos.get(k)[1];
rowMax[i] = Math.max(rowMax[i], mx[k]); // 更新第 i 行的最大 f 值
colMax[j] = Math.max(colMax[j], mx[k]); // 更新第 j 列的最大 f 值
}
}
return ans;
}
}