【数据结构】二叉树——链式结构的实现（代码演示）

news2024/11/27 0:18:14

目录

1 二叉树的链式结构

2  二叉树的创建

 3  二叉树的遍历

3.1 前序遍历

3.1.1运行结果：

3.1.2代码演示图:

3.1.3 演示分析：

3.2 中序遍历

 3.3 后序遍历

3.4 层序遍历

4  判断是否是完全二叉树

5  二叉树节点的个数

5.1 总个数

5.2 叶子节点个数

6  二叉树的深度

7  二叉树的销毁

7.1 二级指针销毁二叉树

7.2 单指针销毁二叉树

8  完整代码

8.1 test.c

8.2 Quene.c

8.3 Quene.h

8.4 运行结果截图

1 二叉树的链式结构

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

该结构包含根节点、左子树(_left)和右子树(_right)以及它们所存储的数据(data)

二叉树是：

  1. 空树
  2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

2  二叉树的创建

// 通过前序遍历的数组"123###45##6##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)  
{

	BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
	if (cur == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	if (*pi >= n || a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}

	cur->_data = a[*pi];
	(*pi)++;

	cur->_left = BinaryTreeCreate(a, n, pi);
	cur->_right = BinaryTreeCreate(a, n, pi);

	return cur;
}

代码表示用前序遍历创建二叉树，参数a表示传进来的数组首元素地址，参数n表示数组长度，参数pi表示下标的地址，这里用指针表示，因为如果不用指针，则递归的过程中重新定义的pi已经不是原来的pi,即找不到下标了。

第一个if语句表示创建失败后执行；第二个if语句表示如果下标pi大于数组长度n或者数组元素等于'#'，下标的位置往后移动一个位置，返回值为NULL; cur->_data = a[*pi]表示将数组中下标为pi的元素赋给当前节点cur->_data；

这里创建了一个二叉树作为例子：

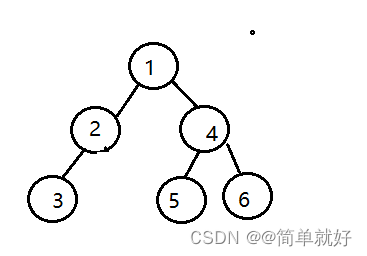
 3  二叉树的遍历

二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉 树中的节点进行相应的操作，并且每个节点只操作一次。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

前序遍历：访问根结点的操作发生在遍历其左右子树之前。根、左子树、右子树。

中序遍历：访问根结点的操作发生在遍历其左右子树之中（间）。左子树、根、右子树。

后序遍历：—访问根结点的操作发生在遍历其左右子树之后。左子树、右子树、根。

层序遍历：先访问根节点，然后从左往右访问第二层，依次访问下面的节点。

3.1 前序遍历


void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
        printf("NULL");
		return ;
	}
//	printf("%c ", root->_data);
	printf("%d ", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}

代码表示：如果节点为空，则返回空值；打印根节点的值，左子树递归，右子树递归。

这里给出运行前序遍历的完整代码：

#define  _CRT_SECURE_NO_WARNINGS
//#include"Heap.h"
#include<time.h>
#include"Quene.h"

//typedef char BTDataType;
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
//	printf("%c ", root->_data);
	printf("%d ", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}

int main()
{
	//BTDataType a[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' };
	BTDataType a[] = { 1,2,3,'#','#','#',4,5,'#','#',6,'#','#' };
	int n = sizeof(a) / sizeof(a[0]);
	int i = 0;
	BTNode* root = BinaryTreeCreate(a, n, &i);

	BinaryTreePrevOrder(root);                 //前序遍历:根，左子树，右子树
	printf("\n");
return 0;
}

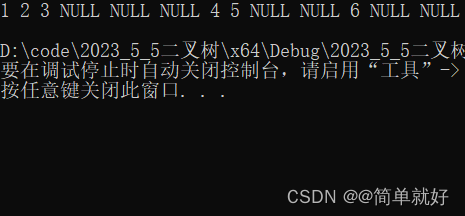
3.1.1运行结果：

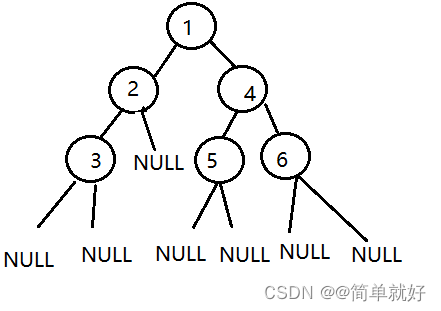
3.1.2代码演示图:

 

3.1.3 演示分析：

(跟着箭头看)首先从根节点“1”开始递归，printf("%d ",root->_data)打印根节点“1”的值;BinaryTreePrevOrder（root->_left）对左子树进行递归;打印左子树根节点 “2"的值;BinaryTreePrevOrder（root->_left）继续对左子树进行递归，打印左子树根节点“3”的值；

BinaryTreePreOrder(root->_left)继续对左子树进行递归，root==NULL,打印空值，返回空,此时函数回到调用它的地方，并销毁栈帧，即回到它的父节点"3"的BinaryTreePrevOrder(root->_left)语句哪里;接下来执行BinaryTreePreOrder(root->_right)语句，root==NULL,打印空值，返回空,此时函数回到调用它的地方，并销毁栈帧，即回到它的父节点"2"的BinaryTreePreOrder(root->_right)语句哪里；然后依此类推。

3.2 中序遍历

void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return ;
	}

	BinaryTreeInOrder(root->_left);
//	printf("%c ", root->_data);
	printf("%d ", root->_data);
	BinaryTreeInOrder(root->_right);
}

其实它的代码和前序遍历差不多，只是中序遍历要先走完左子树，才走根节点，最后右子树。

运行结果：

 3.3 后序遍历

void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return ;
	}
	BinaryTreePostOrder(root->_left);
	BinaryTreePostOrder(root->_right);
	//printf("%c ", root->_data);
	printf("%d ", root->_data);
}

 其实后续遍历的代码和前序遍历的代码差别不大，唯一差别就是，后序遍历是递归完左子树和右子树之后才打印根节点。

3.4 层序遍历

void BinaryTreeLevelOrder(BTNode* root)
{
	Quene qu;
	QueneInit(&qu);
	if(root)
		QuenePush(&qu, root);
	while (!QueneEmpty(&qu))
	{
		BTNode* cur = QueneFront(&qu);  
//		printf("%c ", cur->_data);
		printf("%d ", cur->_data);
		QuenePop(&qu);

		if (cur->_left)
		{
			QuenePush(&qu, cur->_left);
		}
		if (cur->_right)
		{
			QuenePush(&qu, cur->_right);
		}
	}
	printf("\n");
	QuenDestroy(&qu);
}

层序遍历，我采用队列的链式结构对二叉树的节点的值进行存储。

思路：出上一层，带下一层

代码分析：    按照思路，队头先出“1”，然后把“1”的左节点"2"和右节点"4"尾插进队列,然后出“2”，把“2”的左节点“3”尾插进队列，然后队头出“4”，把“4”的左节点“5”和右节点“6”尾插进队列。以此类推。QueneInit(&qu);表示初始化队列"qu";  QuenePush(&qu, root);表示将二叉树的值尾插到队列中；BTNode* cur = QueneFront(&qu);  表示创建一个二叉树结构体类型的节点cur来存放队列首元素的值；    QuenePop(&qu);表示出队列。

4  判断是否是完全二叉树

bool BinaryTreeComplete(BTNode* root)
{
	Quene qu;
	QueneInit(&qu);
if(root)
	QuenePush(&qu, root);

	while (!QueneEmpty(&qu)) 
	{
		BTNode* front = QueneFront(&qu);
		QuenePop(&qu);
		if (front == NULL)               //如果当前节点不为空，则将它的左右节点放入队列
		{
			break;
		}
		else
		{
			QuenePush(&qu, front->_left);
			QuenePush(&qu, front->_right);
		}
	}
	//出到空以后，如果后面全是空，则是完全二叉树
	while (!QueneEmpty(&qu))
	{
		BTNode* front = QueneFront(&qu);
		QuenePop(&qu);
		if (front != NULL)
		{
			QuenDestroy(&qu);
			return false;
		}
	}
	QuenDestroy(&qu);
	return true;

}

思路：二叉树的节点出队列遇到空值以后，往后都是空值则是完全二叉树，否则不是。

代码分析：如果二叉树的当前节点不为空，入队列;如果队列不为空，先出队列，然后将它的左右节点尾插进队列；第二个while哪里，队列不为空，出队列，遇到空值后，往后都是空值，则为完全二叉树，否则不是完全二叉树。

5  二叉树节点的个数

5.1 总个数

int BinaryTreeSize(BTNode* root)
{
	//if (root == NULL)
	//{
	//	return 0;
	//}
	//int left = BinaryTreeSize(root->_left);
	//int right = BinaryTreeSize(root->_right);

	//return left + right +1;//返回总节点个数
	return root==NULL ? 0:BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1; 
}

思路：如果二叉树的节点为空，则返回0，否则计算出左边 + 右边 + 1。

5.2 叶子节点个数

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->_left == NULL && root->_right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

 思路：如果该节点为空，返回0；如果该节点的左右节点都为空，返回1；对左子树和右子树递归。

6  二叉树的深度

int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftHeight = TreeHeight(root->_left);
	int rightHeight = TreeHeight(root->_right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

这里需要注意的是要定义两个整形变量来存放左节点和右节点的个数，如果不定义直接

return TreeHeight(root->_left) >TreeHeight(root->_right) ?  TreeHeight(root->_left)+1: TreeHeight(root->_right)+1;性能会下降很多，因为在"?"前面的递归只是做了比较，并没有保存比较的值，使得出现很多重复的计算，会极大的浪费资源，上一层会连累下一层，每一层都要重复计算。

7  二叉树的销毁

7.1 二级指针销毁二叉树

void BinaryTreeDestory(BTNode** root) //参数root是一个指向指针的指针，因为需要修改每个节点的指针
{
	if (*root)
	{
		BinaryTreeDestory(&(*root)->_left);
		BinaryTreeDestory(&(*root)->_right);
		free(*root);
		*root = NULL;      //防止内存泄露
	}

}

说明：这里使用后续遍历对二叉树的节点进行置空。

BinaryTreeDestroy(&((*root)->left)) 中的 (*root)->left 是一个指向左子树根节点的指针，它的类型为 TreeNode*。因此，我们需要先用 * 运算符解引用 root 指向的地址，得到指向二叉树根节点的指针 *root，然后再使用箭头运算符 -> 访问其左子树，并取其地址作为参数传递给 BinaryTreeDestroy() 函数。

这样做是因为我们需要修改根节点的左子树指针，使其指向空，并释放原来左子树所占用的内存。如果直接传递 (*root)->left 作为参数，则只是将一个指向左子树根节点的临时指针传递给了函数，在函数内部无法修改原来的左子树指针。
 

在这个函数中，使用了一个BTNode**类型的指针作为参数。这个指针指向了二叉树根结点的地址。在函数内部，首先判断当前节点是否为空，如果为空则直接返回。然后递归地销毁当前节点的左子树和右子树，直到最底层的叶子节点。最后释放当前节点所占用的内存，并将其只想空指针以避免野指针。

7.2 单指针销毁二叉树

void TreeDestory(BTNode* root)
{
    if(root==NULL)
        return;
    TreeDestory(root->_left);
    TreeDestory(root->_right);
    free(root);
}

然后再主函数哪里调用TreeDestory()函数之后需要添加"root==NULL"

8  完整代码

8.1 test.c

#define  _CRT_SECURE_NO_WARNINGS
//#include"Heap.h"
#include<time.h>
#include"Quene.h"

//typedef char BTDataType;
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;



// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
//void BinaryTreeDestory(BTNode** root);
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//二叉树的深度
int TreeHeight(BTNode* root);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);


// 判断二叉树是否是完全二叉树
//int BinaryTreeComplete(BTNode* root);
bool BinaryTreeComplete(BTNode* root);

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)  
{

	BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
	if (cur == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	if (*pi >= n || a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}

	cur->_data = a[*pi];
	(*pi)++;

	cur->_left = BinaryTreeCreate(a, n, pi);
	cur->_right = BinaryTreeCreate(a, n, pi);

	return cur;
}

//void BinaryTreeDestory(BTNode** root) //参数root是一个指向指针的指针，因为需要修改每个节点的指针
//{
//	if (*root)
//	{
//		BinaryTreeDestory(&(*root)->_left);
//		BinaryTreeDestory(&(*root)->_right);
//		free(*root);
//		*root = NULL;      //防止内存泄露
//	}
//
//}

void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeDestory(root->_left);
	BinaryTreeDestory(root->_right);
	free(root);
}

int BinaryTreeSize(BTNode* root)
{
	//if (root == NULL)
	//{
	//	return 0;
	//}
	//int left = BinaryTreeSize(root->_left);
	//int right = BinaryTreeSize(root->_right);

	//return left + right +1;//返回总节点个数
	return root==NULL ? 0:BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1; 
}

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->_left == NULL && root->_right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->_data == x)
	{
		return root;
	}

	BTNode* ret1 = BinaryTreeFind(root->_left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = BinaryTreeFind(root->_right, x);
	if (ret2)
		return ret2;

	return NULL;
}

int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftHeight = TreeHeight(root->_left);
	int rightHeight = TreeHeight(root->_right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
	//	printf("NULL ");
		return ;
	}
//	printf("%c ", root->_data);
	printf("%d ", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}

void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
//		printf("NULL ");
		return ;
	}

	BinaryTreeInOrder(root->_left);
//	printf("%c ", root->_data);
	printf("%d ", root->_data);
	BinaryTreeInOrder(root->_right);
}

void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return ;
	}
	BinaryTreePostOrder(root->_left);
	BinaryTreePostOrder(root->_right);
	//printf("%c ", root->_data);
	printf("%d ", root->_data);
}

void BinaryTreeLevelOrder(BTNode* root)
{
	Quene qu;
	QueneInit(&qu);
	if(root)
		QuenePush(&qu, root);
	while (!QueneEmpty(&qu))
	{
		BTNode* cur = QueneFront(&qu);  
//		printf("%c ", cur->_data);
		printf("%d ", cur->_data);
		QuenePop(&qu);

		if (cur->_left)
		{
			QuenePush(&qu, cur->_left);
		}
		if (cur->_right)
		{
			QuenePush(&qu, cur->_right);
		}
	}
	printf("\n");
	QuenDestroy(&qu);
}

//int BinaryTreeComplete(BTNode* root) 
//{
//	Quene qu;
//	BTNode* cur;
//	int tag = 0;
//	QueneInit(&qu);
//	QuenePush(&qu, root);
//
//	while (!QueneEmpty(&qu))
//	{
//		cur = QueneFront(&qu);
		printf("%c ", cur->_data);
//		printf("%d ", cur->_data);
//		if (cur->_right && !cur->_left)
//		{
//			return 0;
//		}
//		if (tag && (cur->_left || cur->_right))   //tag?
//		{
//			return 0;
//		}
//
//
//		if (cur->_left)
//		{
//			QuenePush(&qu, cur->_left);
//		}
//
//		if (cur->_right)
//		{
//			QuenePush(&qu, cur->_right);
//		}
//		else
//		{
//			tag = 1;
//		}
//		QuenePop(&qu);
//	}
//
//	QuenDestroy(&qu);
//	return 1;
//}

bool BinaryTreeComplete(BTNode* root)
{
	Quene qu;
	QueneInit(&qu);
	QuenePush(&qu, root);

	while (!QueneEmpty(&qu)) 
	{
		BTNode* front = QueneFront(&qu);
		QuenePop(&qu);
		if (front == NULL)               //如果当前节点不为空，则将它的左右节点放入队列
		{
			break;
		}
		else
		{
			QuenePush(&qu, front->_left);
			QuenePush(&qu, front->_right);
		}
	}
	//出到空以后，如果后面全是空，则是完全二叉树
	while (!QueneEmpty(&qu))
	{
		BTNode* front = QueneFront(&qu);
		QuenePop(&qu);
		if (front != NULL)
		{
			QuenDestroy(&qu);
			return false;
		}
	}
	QuenDestroy(&qu);
	return true;

}


int main()
{
	//BTDataType a[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' };
	BTDataType a[] = { 1,2,3,'#','#','#',4,5,'#','#',6,'#','#' };
	int n = sizeof(a) / sizeof(a[0]);
	int i = 0;
	BTNode* root = BinaryTreeCreate(a, n, &i);

	BinaryTreePrevOrder(root);                 //前序遍历:根，左子树，右子树
	printf("\n");

	BinaryTreeInOrder(root);				    //中序遍历:左子树，根，右子树
	printf("\n");

	BinaryTreePostOrder(root);                  //后序遍历:左子树，右子树，根
	printf("\n");


	BinaryTreeLevelOrder(root);                 //层序遍历
	printf("\n");

	printf("Size:%d\n", BinaryTreeSize(root));
	printf("leafsize:%d\n", BinaryTreeLeafSize(root));
	printf("TreeHeight:%d\n", TreeHeight(root));
	//int iscompleate= BinaryTreeComplete(root);
	//if (iscompleate == 1)
	//	printf("是完全二叉树\n");
	//else
	//	printf("不是完全二叉树\n");

	printf("TreeComplete:%d \n", BinaryTreeComplete(root));
	BinaryTreeDestory(root);
	root = NULL;
	return 0;

}

8.2 Quene.c

#define  _CRT_SECURE_NO_WARNINGS
#include"Quene.h"



void QueneInit(Quene* pq)              
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QuenDestroy(Quene* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* del = cur;
		cur = cur->next;
		free(del);
	}
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QuenePush(Quene* pq, QDataType x)               //进队列
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode)); //插入值时开辟空间
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->next = NULL; 
	newnode->data = x;
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;                        //尾插到pq->tail后面
		pq->tail = newnode;                              //重新调整pq->tail的位置
	}
	pq->size++;                                      //记录数据
}

void QuenePop(Quene* pq)                             //出队列
{
	assert(pq);                                      //判断队列是否为空，假如传进来的是一个空队列则不能出队列
	assert(!QueneEmpty(pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* del = pq->head;
		pq->head = pq->head->next;
		free(del);
	}
	pq->size--;
}

QDataType QueneFront(Quene* pq)
{
	assert(pq);
	assert(!QueneEmpty(pq));
	return pq->head->data;
}
QDataType QueneBack(Quene* pq)
{
	assert(pq);
	assert(!QueneEmpty(pq));
	return pq->tail->data;
}

bool QueneEmpty(Quene* pq)
{
	assert(pq);
	return pq->head == NULL && pq->tail == NULL;
}
int QueneSize(Quene* pq)
{
	assert(pq);
	return pq->size;
}

8.3 Quene.h

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

//前置声明
struct BinaryTreeNode;

typedef struct BinaryTreeNode* QDataType;                   //定义队列数据类型
typedef struct QueneNode
{

	QDataType data;                      //队列中的数据
	struct QueneNode* next;              //队列的下一个节点
}QNode;

typedef struct Queue
{
	QNode* head;                   //队头
	QNode* tail;                   //队尾
	int size;                     //队列的长度

}Quene;

void QueneInit(Quene* pq);        //队列初始化
void QuenDestroy(Quene* pq);      //队列的销毁
void QuenePush(Quene* pq, QDataType x);   //数据进队列
void QuenePop(Quene* pq);                 //数据出队列
QDataType QueneFront(Quene* pq);          //队头的值
QDataType QueneBack(Quene* pq);           //队尾的值

bool QueneEmpty(Quene* ps);               //队列判空
int QueneSize(Quene* pq);                 //队列大小

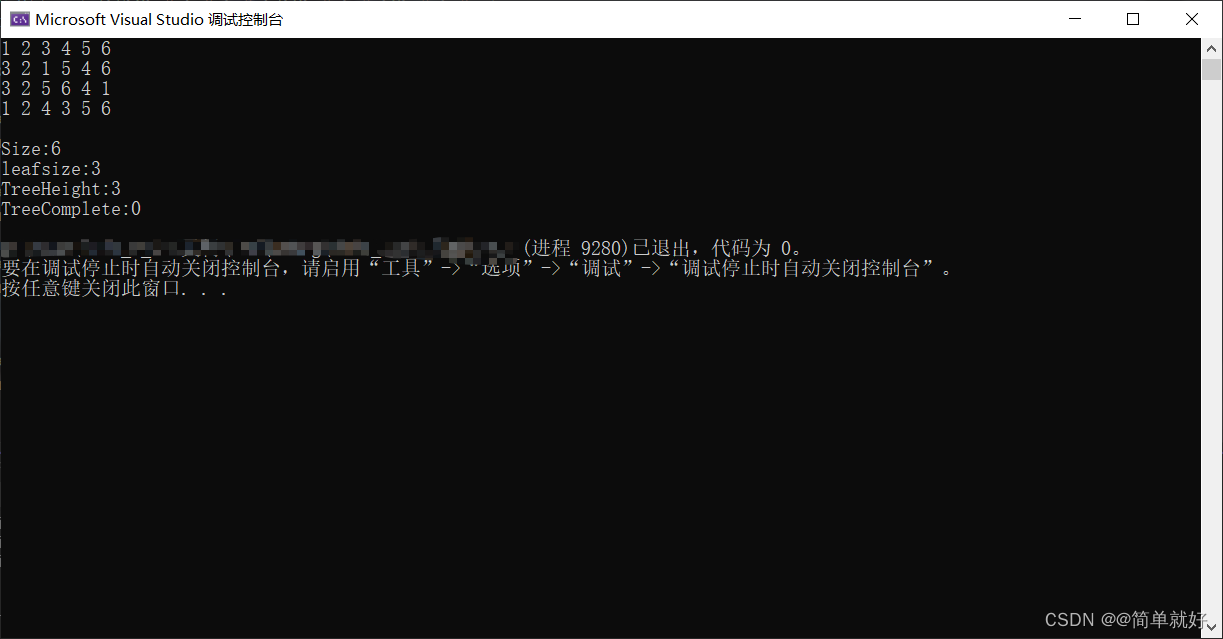
8.4 运行结果截图

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/585542.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Electron-Builder Windows系统代码签名

Electron-Builder Windows系统代码签名

前言 项目打包签名是两年前做的了&#xff0c;使用Electron-Bulder&#xff0c;打包工具版本迭代较少&#xff0c;倒是electron版本更新飞快&#xff0c;目前官方推荐使用Electron Forge进行打包&#xff0c;后续再对两者进行对比&#xff0c;重新整理现在的实现方案。 签名简…
阅读更多...
微信扫码授权到登录网页，中间究竟发生了什么？

微信扫码授权到登录网页，中间究竟发生了什么？

关于我昨天突然接到神秘“面试”&#xff1a;微信扫码授权登录的实现逻辑是神魔&#xff1f;在这个扫码授权的过程中客户端、服务端、微信平台都做了些神魔&#xff1f;二维码里面又有哪些信息&#xff1f; 从手机微信扫一扫二维码到登录个人的知乎账户&#xff0c;中间究竟发生…
阅读更多...
智警杯赛前学习1.2--excel统计函数

智警杯赛前学习1.2--excel统计函数

常用统计函数 count countif&#xff08;区域&#xff0c;条件&#xff09; countifs&#xff08;区域&#xff0c;条件&#xff0c;区域&#xff0c;条件&#xff09; 求和函数 sum sumif&#xff08;区域&#xff0c;条件&#xff0c;[求和区域]&#xff09; sumifs&#xff…
阅读更多...
AOP日志功能实现

AOP日志功能实现

AOP日志功能实现 1、添加两个工具类2、新建一个接口为 LogAnnotation3、新建一个类 LogAspect4、使用自定义注解 LogAnnotation5、运行结果6、项目结构 转载自b站&#xff1a;码神之路 1、添加两个工具类 HttpContextUtils 用于获取当前请求的 HttpServletRequest 对象&#xf…
阅读更多...
Pycharm中安装jupyter 以及一些会遇到的问题

Pycharm中安装jupyter 以及一些会遇到的问题

1、确保电脑安装了 anaconda 和jupyter notebook 2、在命令行 启动jupyter Notebook &#xff08;启动后不要关闭这个命令窗口&#xff09; 命令&#xff1a;juputer Notebook 成功运行后的网页界面&#xff1a; 3、打开Pycharm 创建新的项目 &#xff08;注意是Conda) 4、 创…
阅读更多...
【微信小程序开发小白零基础入门】微信小程序入门【建议收藏】

【微信小程序开发小白零基础入门】微信小程序入门【建议收藏】

微信小程序入门 文章目录 微信小程序入门前言一、小程序的概述1.小程序简介2.小程序诞生3.小程序功能4.小程序创建步骤 二、小程序的准备工作1.注册开发者账号2.小程序信息完善3.成员管理 三、小程序的开发工具3.其他辅助工具 四、推荐小程序&#xff08;欢迎各位大佬指导&…
阅读更多...
STM32F4_常用存储器简介

STM32F4_常用存储器简介

目录 1. 存储器的种类 单片机和电脑一样&#xff0c;其内核分别为ARM和CPU(CPU通常是不具备存储功能的)&#xff0c;内核是用来进行数据的运算和处理的。内核处理数据的来源就是存储器。 1. 存储器的种类 RAM存储器&#xff1a; RAM是 “Random Access Memory”的缩写&#x…
阅读更多...
Java 集合、数组、字符串的相互转换（关于list.toArray(new String[0])的源码分析）

Java 集合、数组、字符串的相互转换（关于list.toArray(new String[0])的源码分析）

在 Java 中&#xff0c;可以通过以下方式实现集合、数组和字符串之间的相互转换。 一、集合和数组的相互转化 ①、将集合转为数组&#xff1a;&#xff08;toArray 方法&#xff09; List<String> list new ArrayList<>(); list.add("apple"); lis…
阅读更多...
异构跨库数据同步还在用Datax?来看看这几个开源的同步方案

异构跨库数据同步还在用Datax?来看看这几个开源的同步方案

在遇到跨库或者异库数据同步时&#xff0c;我们一般都会借助ETL工具来实现数据同步功能。比如目前大家较为熟知的Kettle和Datax。但是&#xff0c;这两个需要定时去查询数据库的数据&#xff0c;会存在一定的延迟&#xff0c;而且&#xff0c;默认采用全量同步的方式&#xff0…
阅读更多...
Java Spring概述

Java Spring概述

文章目录 1、Spring是什么&#xff1f;2、Spring 的狭义和广义3、Spring Framework特点4、Spring模块组成5、Spring6版本要求 1、Spring是什么&#xff1f; Spring 是一款主流的 Java EE 轻量级开源框架 &#xff0c;Spring 由“Spring 之父”Rod Johnson 提出并创立&#xff…
阅读更多...
AD原理图元器件封装绘制

AD原理图元器件封装绘制

元器件封装界面 1.元器件可以新建原理图库&#xff0c;然后在新建的库中添加 2.采用下图中的方式&#xff0c;随便右键某个库中的元器件&#xff0c;选择“Edit…”&#xff0c;进入到元器件封装绘制界面 元器件封装设计步骤 1.点击工具——新器件 输入新器件ID&#xff0c…
阅读更多...
性能测试监控平台：InfluxDB+Grafana+Jmeter

性能测试监控平台：InfluxDB+Grafana+Jmeter

前言 性能测试工具jmeter自带的监视器对性能测试结果的实时展示&#xff0c;在Windows系统下的GUI模式运行&#xff0c;渲染和效果不是太好&#xff0c;在linux环境下又无法实时可视化。 2023年最新出炉性能测试教程&#xff0c;真实企业性能压测全流程项目实战训练大合集&am…
阅读更多...
软件测试：测试用例详解

软件测试：测试用例详解

一、通用测试用例八要素 　 1、用例编号&#xff1b; 　　 2、测试项目&#xff1b; 　 3、测试标题&#xff1b; 4、重要级别&#xff1b; 　　 5、预置条件&#xff1b; 　　 6、测试输入&#xff1b; 　　 7、操作步骤&#xff1b; 　　 8、预期输出 二、具体分析通…
阅读更多...
微信支付Native下单API V3接口开发详解

微信支付Native下单API V3接口开发详解

这几天做微信支付Native下单接口调用、签名这块&#xff0c;弄的我焦头烂额&#xff0c;翻了很多网上配置&#xff0c;各有不同&#xff0c;写的不清不楚&#xff0c;只能自己慢慢研究&#xff0c;尝试了无数种解决坑的方案&#xff0c;嚼文咬字看官方的文档调试&#xff0c;文…
阅读更多...
从零开始学Android开发期末复习重点

从零开始学Android开发期末复习重点

目录 前言作业&#xff11;作业&#xff12;作业&#xff13;作业4作业5作业6 前言 物联网应用技术课程期末复习重点——学习通作业&#xff1a; 操作系统&#xff1a;Ubuntu22.04 作业&#xff11; 简述Android系统架构。 Android 的系统架构和它的操作系统一样&#xff…
阅读更多...
前端开发需要学什么？零基础前端学习路线看这一篇就够了！

前端开发需要学什么？零基础前端学习路线看这一篇就够了！

是的&#xff0c;自学前端可以帮助您找到工作&#xff0c;参加培训是根据个人学习能力和经济实力来自己决定的。前端开发是一个相对容易入门的领域&#xff0c;并且许多人通过自学成功地找到了前端开发的工作。以下是好程序员的一些建议&#xff0c;可以帮助您在自学前端时提高…
阅读更多...
离线语音控制新方案，NRK3303语音识别芯片在智能风扇的应用

离线语音控制新方案，NRK3303语音识别芯片在智能风扇的应用

随着科技的不断发展&#xff0c;智能家居已经成为人们日常生活中不可或缺的一部分&#xff0c;涌现出越来越多的智能设备&#xff0c;如智能门锁、智能灯泡、智能冰箱等&#xff0c;这些设备为人们的生活带来了更多的便利和创新。其中作为常见的风扇通过添加智能语音控制功能&a…
阅读更多...
分布式运用之Filebeat+Kafka+ELK 的服务部署

分布式运用之Filebeat+Kafka+ELK 的服务部署

1. Kafka 架构深入了解 1.1 Kafka 工作流程及文件存储机制 Kafka 中消息是以 topic 进行分类的&#xff0c;生产者生产消息&#xff0c;消费者消费消息&#xff0c;都是面向 topic 的。 topic 是逻辑上的概念&#xff0c;而 partition 是物理上的概念&#xff0c;每个 parti…
阅读更多...
路径规划算法：基于哈里斯鹰优化的路径规划算法- 附代码

路径规划算法：基于哈里斯鹰优化的路径规划算法- 附代码

路径规划算法&#xff1a;基于哈里斯鹰优化的路径规划算法- 附代码 文章目录 路径规划算法&#xff1a;基于哈里斯鹰优化的路径规划算法- 附代码1.算法原理1.1 环境设定1.2 约束条件1.3 适应度函数 2.算法结果3.MATLAB代码4.参考文献 摘要&#xff1a;本文主要介绍利用智能优化…
阅读更多...
leetcode 2.两数相加（链表操作）

leetcode 2.两数相加（链表操作）

题目描述跳转到leetcode 给你两个 非空 的链表&#xff0c;表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的&#xff0c;并且每个节点只能存储 一位 数字。 请你将两个数相加&#xff0c;并以相同形式返回一个表示和的链表。 你可以假设除了数字 0 之外&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023