栈
顺序栈
栈(Stack)是限定仅在表的一端进行插入或删除操作的线性表。通常称插入删除的一端为栈顶(top),另一端称为栈底(bottom)。
typedef struct{
DataType data[StackSize];
int top;
}SeqStack;
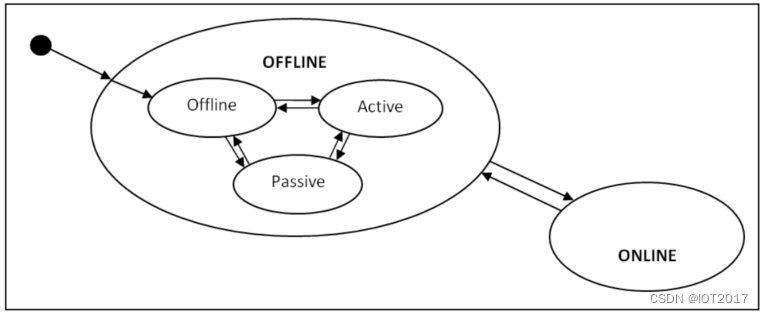
基本操作

示意
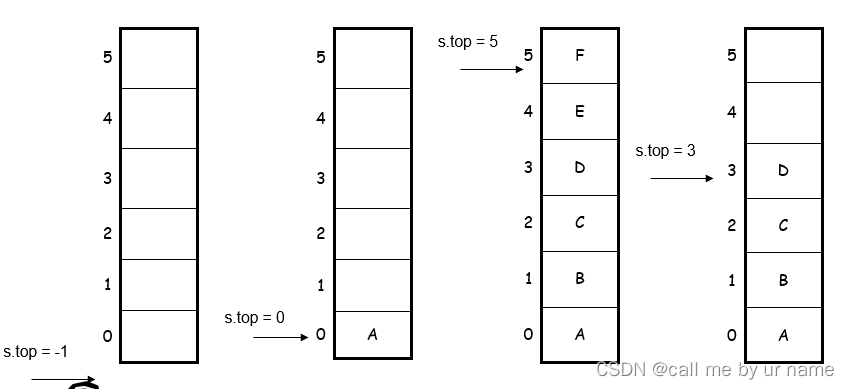
在没有元素时,top=-1,栈的第一个元素的位序是0
基本操作实现
入栈
void Push(seqStack &S, DataType x)
{ if(StackFull(S))
Error(“Stack overflow”);
S.data[++S->top]=x;
}
出栈
DataType Pop(seqStack &S)
{ if(StackEmpty(S))
Error(“Stack underflow”);
return S.data[S->top--];
}
链栈
typedef struct Stacknode{
DataType data
struct stacknode *next
}StackNode;
typedef struct{
StackNode *top; //栈顶指针
}LinkStack;
基本操作的实现
入栈
void Push(LinkStack &S, DataType x){
StackNode *p=(StackNode*)malloc(sizeof(StackNode));
p->data=x;
p->next=S->top;
S->top=p;
}
出栈
DataType Pop(LinkStack &S){
DataType x;
StackNode *p=S->top;
if(StackEmpty(S))Error(“Stack underflow”);
x=p->data;
s->top=p->next;
free(p);
return x;
}
需要注意的是:
p
−
>
n
e
x
t
p->next
p−>next指向下面的元素以栈顶为上,栈底为下
顺序栈和链栈的比较
时间效率:
- 所有操作都只需常数时间
- 顺序栈和链式栈在时间效率上难分伯仲
空间效率:
- 顺序栈须说明一个固定的长度
- 链式栈的长度可变,但增加结构性开销
迷宫问题
顺序栈实现
// 定义迷宫中通道块的数据结构
typedef struct {
int ord; // 通道块在路经上的“序号”
PosType seat; // 通道块在迷宫中的“坐标位置”
int di; // 从此通道块走向下一通道块的“方向”
} SElemType;
// 寻找从起点 start 到终点 end 的路径
Status MazePath(MazeType maze, PosType start, PosType end) {
SqStack S;
InitStack(S); // 初始化栈
PosType curpos = start; // 设定“当前位置”为“入口位置”
int curstep = 1; // 探索第一步
do {
if (Pass(curpos)) {
// 当前位置可以通过,即是未曾走到过的通道块
FootPrint(curpos); // 留下足迹
SElemType e = {curstep, curpos, 1}; // 新建通道块
Push(S, e); // 加入路径
if (curpos == end) {
return (TRUE); // 到达出口(终点)
}
curpos = NextPos(curpos, 1); // 下一位置是当前位置的东邻
curstep++; // 探索下一步
} else {
// 当前位置不能通过
if (!StackEmpty(S)) {
SElemType e;
Pop(S, e);
while (e.di==4 && !StackEmpty(S)) {
MarkPrint(e.seat); Pop(S, e); // 留下不能通过的标记,并退回一步
}
if (e.di < 4) {
e.di++;
Push(S, e); // 换下一个方向探索
curpos = NextPos(e.seat, e.di); // 设定当前位置是该新方向上的相邻块
}
}
}
} while (!StackEmpty(S));
return (FALSE); // 无法从起点到达终点
}
表达式求值
OperandType EvaluateExpression() {
//算术表达式求值的算符优先算法。设OPTR和OPND
//分别为运算符栈和运算数栈,OP为运算符集合。
InitStack (OPTR); Push(OPTR,’#’);
InitStack (OPND); c=getchar();
while (c!=‘#’||GetTop(OPTR)!=‘#’) {
if (!In (c, OP)) { Push (OPND, c); c= getchar();}
//不是运算符则进栈
else
switch (Precede( GetTop (OPTR), c)){
case’<’: //栈顶元素优先权低
Push (OPTR, c); c= getchar();
break;
case’=’: //脱括号并接受下一字符
Pop (OPTR, c); c= getchar();
break;
case’>’: //退栈并将运算结果入栈
Pop (OPTR, theta);
Pop (OPND, b); Pop (OPND, a);
Push (OPND, Operate (a,
theta, b));
break;
}//switch
}//while
return GetTop(OPND);
}//EvaluateExpression
递归
- 问题的定义是递归的。例如,数学中的阶乘函数、二阶Fibonacci函数等。
- 有的数据结构,如二叉树、广义表等,由于结构本身固有的递归特性,则它们的操作可递归的描述。
- 有些问题,虽然问题本身没有明显的递归结构,但用递归求解比迭代求解更简单。如八皇后问题、Hanoi塔问题等
没什么好说的这一块
队列
先进先出
链队列
typedef struct QNode {// 结点类型
QElemType data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct { // 链队列类型
QueuePtr front; // 队头指针
QueuePtr rear; // 队尾指针
} LinkQueue;
示意图
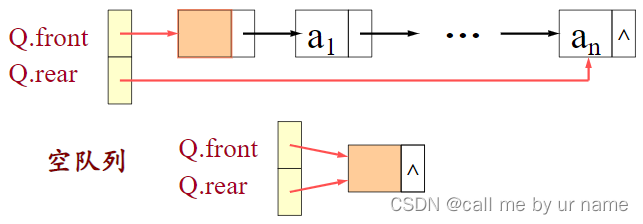
易知:队列的next指针是指向当前元素在队列中后面的元素
基本操作

入队列
Status EnQueue (LinkQueue &Q, QElemType e) {
// 插入元素e为Q的新的队尾元素
p = (QueuePtr) malloc (sizeof (QNode));
if(!p) exit (OVERFLOW); //存储分配失败
p->data = e; p->next = NULL;
Q.rear->next = p; Q.rear = p;
return OK;
}
其中,自己在写算法时也要注意添加类似if(!p) exit (OVERFLOW); //存储分配失败这样的判断异常的语句
出队列
Status DeQueue (LinkQueue &Q, QElemType &e) {
// 若队列不空,则删除Q的队头元素,
//用 e 返回其值,并返回OK;否则返回ERROR
if (Q.front == Q.rear) return ERROR;
p = Q.front->next; e = p->data;
Q.front->next = p->next;
if (Q.rear == p) Q.rear = Q.front;
free (p); return OK;
}
判断异常if (Q.front == Q.rear) return ERROR;
这一步的特判if (Q.rear == p) Q.rear = Q.front;
顺序队列
循环
#define MAXQSIZE 100 //最大队列长度
typedef struct {
QElemType *base; // 动态分配存储空间
int front; // 头指针,若队列不空,
// 指向队列头元素
int rear; // 尾指针,若队列不空,
//指向队列尾元素 的下一个位置
} SqQueue;
这里的
r
e
a
r
rear
rear是指向队尾元素的下一个位置
链队列的
r
e
a
r
rear
rear指向队尾元素
基本操作
大体同链队列
入队列
Status EnQueue (SqQueue &Q, ElemType e) {
// 插入元素e为Q的新的队尾元素
if ((Q.rear+1) % MAXQSIZE == Q.front) return ERROR; //队列满
Q.base[Q.rear] = e;
Q.rear = (Q.rear+1) % MAXQSIZE;
return OK;
}
好好理解一下这个,(Q.rear+1) % MAXQSIZE的意思(结合下面Q.rear = (Q.rear+1) % MAXQSIZE;)
出队列
Status DeQueue (SqQueue &Q, ElemType &e) {
// 若队列不空,则删除Q的队头元素,
// 用e返回其值,并返回OK; 否则返回ERROR
if (Q.front == Q.rear) return ERROR;
e = Q.base[Q.front];
Q.front = (Q.front+1) % MAXQSIZE;
return OK;
}
同样注意:Q.front = (Q.front+1) % MAXQSIZE;
银行问题(离散事件模拟)
假设某银行有4个窗口营业,从早晨银行开门起不断有客户进入银行。每个窗口每一时刻只能接待一个客户,对于刚进入银行的客户,如果某个窗口的业务员正空闲,则可上前办理业务;反之,若4个窗口均有客户所占,他会排在人数最少的队伍后面。现要编制一个程序以模拟银行的这种业务活动并计算一天客户在银行逗留的平均时间。
思路
- 大体思路是事件驱动
代码
typedef struct {
int OccurTime; //事件发生时刻
int NType; //事件类型,0表示到达事件,1至4表示四个窗口的离开事件
}Event, ElemType; //事件类型,有序链表LinkList的数据元素类型
typedef LinkList EventList //事件链表类型,定义为有序链表
typedef struct {
int ArrivalTime; //到达时刻
int Duration; //办理事务所需时间
}QElemType; //队列的数据元素类型
EventList ev; //事件表
Event en; //事件
LinkQueue q[5]; //4个客户队列
QElemType customer; //客户记录
int TotalTime, CustomerNum; //累计客户逗留时间,客户数
int com (Event a, Event b); //依事件a的发生时刻<或=或>事件b的发生时刻分别返回-1或0或1
void OpenForDay() { //初始化操作
TotalTime=0; CustomerNum=0; //初始化累计时间和客户数为0
InitList (ev); //初始化事件链表为空表
en.OccurTime=0; en.NType=0; //设定第一个客户到达事件
OrderInsert (ev, en, cmp); //插入事件表
for (i=1; i<=4; ++i) InitQueue (q[i]); //置空队列
}//OpenForDay
void CustomerArrived() {
//处理客户到达事件,en.NType=0。
++CustomerNum;
Random (durtime, intertime); //生成随机数
t=en.OccurTime+ intertime; //下一客户到达时刻
if (t<CloseTime) //银行尚未关门,插入事件表
OrderInsert (ev, (t, 0), cmp);
i=Minimum (q); //求长度最短队列
EnQueue (q[i], (en.OccurTime, durtime));
if(QueueLength (q[i])==1)
OrderInsert (ev, (en.OccurTime + durtime, i), cmp); //设定第i队列的一个离开事件并插入事件表
}// CustomerArrived
void CustomerDeparture() {
//处理客户离开事件,en.NType>0。
i=en.NType; DelQueue (q[i], customer); //删除第i队列的排头客户
TotalTime+=en.OccurTime- customer.Arrivaltime; //累计客户逗留时间
if (!QueueEmpty(q[i])) //设定第i队列的一个离开事件并插入事件表
GetHead (q[i], customer);
OrderInsert (ev, (en.OccurTime + custom.Duration, i), (*cmp)());
}// CustomerDeparture
void Bank_ Simulation (int CloseTime) {
OpenForDay();
while (! ListEmpty(ev) ) { //初始化
DelFirst (GetHead (ev), p);
en=GetCurElem(p);
if(en.NType==0) CustomerArrived(); //处理客户到达事件
else CustomerDeparture() ; //处理客户离开事件
} //计算平均逗留时间
printf(“The Average Time is %f\n”, (float)TotalTime/CustomerNum);
}// Bank_ Simulation
习题
3.2
简述栈和线性表的差别
题解
线性表是具有相同特性的数据元素的一个有限序列。栈是限定仅在表尾进行插入或删除操作的线性表
3.18

这道题看题目,思路上没什么难度。但是需要注意一下,写算法的细节:
- InitStack(s)
- ElemType x
- 最后
if(s.size!=0) return False;(左右括号数量不等),我觉得我个人,很可能写完while和switch语句后,就没考虑到这个细节,值得重新写一遍
3.21


3.32
试利用循环队列编写求 k k k阶斐波那契序列中前 n + 1 n+1 n+1 项 ( f 0 , f 1 , … , f n ) (f_0, f_1 ,…, f_n) (f0,f1,…,fn) 的算法,要求满足: f n ≤ m a x , f n + 1 > m a x f_n≤max, f_{n+1}>max fn≤max,fn+1>max,其中 m a x max max 为某个约定的常数。(注意:本题所用循环队列的容量仅为 k k k,则在算法执行结束时,留在循环队列中的元素应是所求 k k k阶斐波那契序列中的最后 k k k项 f n − k + 1 … … f n f_{n-k+1}……f_n fn−k+1……fn)
long Fib_CirQueue(long Q[], int k, int& rear, int& n, long max) {
// 使用循环队列Q[k]计算k阶斐波那契数fn,要求fn是不超过max的最大的斐波那契数,
// 函数返回计算结果,rear是队尾指针,指向实际队尾位置。
long sum; // sum为计算过程中的中间变量,记录前k项斐波那契数的和
int i; // 循环计数器
// 给前0~k-1项赋初值
for (i = 0; i < k - 1; i++) {
Q[i] = 0;
}
Q[k - 1] = 1; // 第k项斐波那契数初始化为1
rear = n = k - 1; // 队尾指针,指示实际队尾位置;n为当前fj计数,初始值为k-1
sum = 0; // 初始化sum为0,开始计算第k项斐波那契数
while (1) {
// 累加前k项的斐波那契数的值
for (i = 0; i < k; i++) {
sum = sum + Q[(rear - i + k) % k];
}
if (sum > max) {
break; // 若计算出来的斐波那契数超过了max,则退出循环
}
n++; // 计数器自增1,记录当前计算到了第几项斐波那契数
rear = (rear + 1) % k; // 队列中仅存入到fn项,队尾指针向后移动
Q[rear] = sum; // 将计算结果存入循环队列中,并取代已无用的项
}
return Q[rear]; // 返回计算结果
}
这道题有点复杂,主要是 k k k阶斐波那契数列的概念