1题目
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]
提示:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
2链接
题目链接:40. 组合总和 II - 力扣(LeetCode)
视频链接:回溯算法中的去重,树层去重树枝去重,你弄清楚了没?| LeetCode:40.组合总和II_哔哩哔哩_bilibili
3解题思路
本题与其他组合不一样的地方在于:
- 本题candidates 中的每个元素在每个组合中只能使用一次。
- 本题数组candidates的元素是有重复的,而39.组合总和 (opens new window)是无重复元素的数组candidates
本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合。把所有组合求出来,再用set或者map去重,这么做很容易超时!
所谓去重,其实就是使用过的元素不能重复选取。那么问题来了,我们是要同一树层上使用过,还是同一树枝上使用过呢?题目说,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了):

回溯三部曲:
1、确定参数和返回值
path和result与前面的一些题目相同,除此之外,本题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。这个集合去重的重任就是used来完成的。
vector<vector<int>> result; // 存放组合集合
vector<int> path; // 符合条件的组合
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {2、确定终止条件
终止条件为 sum > target 和 sum == target。
sum > target 这个条件其实可以省略,因为在递归单层遍历的时候,会有剪枝的操作,下面会介绍到。
if (sum > target) { // 这个条件其实可以省略
return;
}
if (sum == target) {
result.push_back(path);
return;
}3、确定单层递归逻辑
前面提到:要去重的是“同一树层上的使用过”。那么如何判断同一树层上元素(相同的元素)是否使用过了呢。
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。
此时for循环里就应该做continue的操作。
这块比较抽象,如图:
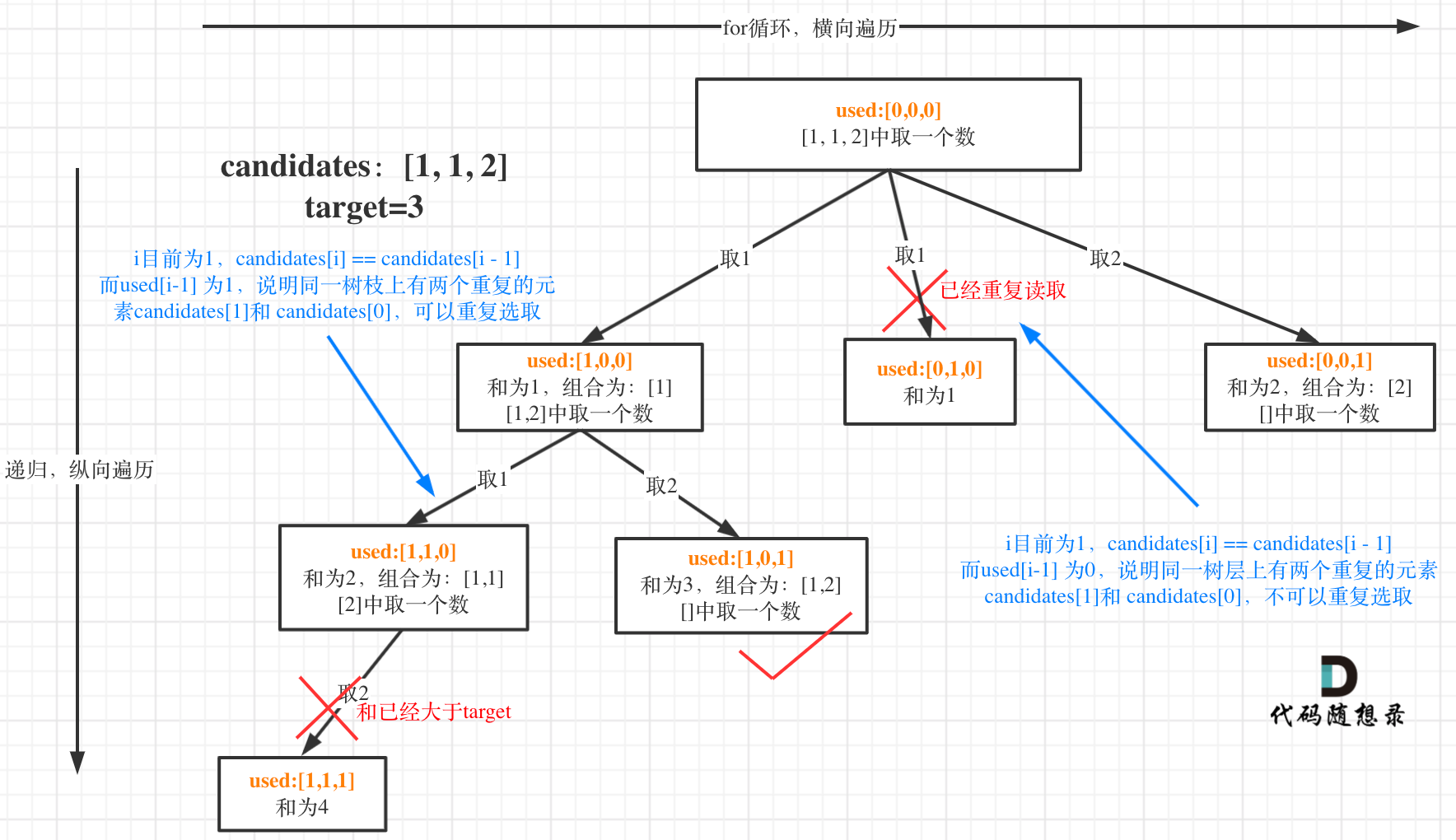
可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = true;
backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1:这里是i+1,每个数字在每个组合中只能使用一次
used[i] = false;
sum -= candidates[i];
path.pop_back();
}注意sum + candidates[i] <= target为剪枝操作
4代码
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
if (sum > target) return ;
if (sum == target) {
result.push_back(path);
return ;
}
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if (i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false) {
continue;
}
path.push_back(candidates[i]);
sum += candidates[i];
used[i] = true;
backtracking(candidates, target, sum, i+1, used);
path.pop_back();
sum -= candidates[i];
used[i] = false;
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(), false);
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0, used);
return result;
}
};