以下内容大部分来源于《MATLAB智能算法30个案例分析》,仅为学习交流所用。
1 理论基础
1.1 遗传算法早熟问题
遗传算法是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应的全局优化概率搜索算法。由于优化时不依赖于梯度,具有很强的鲁棒性和全局搜索能力,因此,被广泛应用于机器学习、模式识别、数学规划等领域。然而,随着遗传算法的广泛应用以及研究的深入,其诸多缺陷与不足也暴露出来,例如,早熟收敛问题。
未成熟收敛是遗传算法中不可忽视的现象,主要表现在群体中的所有个体都趋于同一状态而停止进化,算法最终不能给出令人满意的解。未成熟收敛的发生主要和下列几个方面有关:
(1)选择操作是根据当前群体中个体的适应度值所决定的概率进行的,当群体中存在个别超常个体时(该个体的适应度比其他个体高得多),该个体在选择算子作用下将会多次被选中,下一代群体很快被该个体所控制,群体中失去竞争性,从而导致群体停滞不前。
(2)交叉和变异操作发生的频度是受交叉概率Pe和变异概率Pm控制的。Pe和Pm的恰当设定涉及遗传算法全局搜索和局部搜索能力的均衡,进化搜索的最终结果对Pe、Pm的取值相当敏感,不同的Pe、Pm取值很可能会导致不同的计算结果。
(3)群体规模对遗传算法的优化性能也有较大的影响。当群体规模较小时,群体中多样性程度低,个体之间竞争性较弱,随着进化的进行,群体很快趋于单一化,交叉操作产生新个体的作用渐趋消失,群体的更新只靠变异操作来维持,群体很快终止进化;当群体规模取值较大时,势必造成计算量的增加,计算效率受到影响。
(4)遗传算法常用的终止判据是,当迭代次数到达人为规定的最大遗传代数时,则终止进化。如迭代次数过少,进化不充分,也会造成未成熟收敛。为克服未成熟收敛,许多学者对算法改进进行了一些有益的探索,特别对遗传控制参数的设定,提出了自适应的交叉和变异,并获得了一些有益的结论。但是,遗传算法的未成熟收敛与上述诸多因素有关,在应用遗传算法解决实际问题时,控制参数如何设定,遗传算子如何设计往往是根据实际问题试探性地给出,不恰当的设定会在很大程度上影响算法的性能。
1.2 多种群遗传算法概述
针对遗传算法所存在的上述问题,一种多种群遗传算法(multiple population GA, MPGA)可以用来取代常规的标准遗传算法(SGA)。MPGA在SGA的基础上主要引入了以下几个概念:
(1)突破SGA仅靠单个群体进行遗传进化的框架,引入多个种群同时进行优化搜索;不同的种群赋以不同的控制参数,实现不同的搜索目的。
(2)各个种群之间通过移民算子进行联系,实现多种群的协同进化;最优解的获取是多个种群协同进化的综合结果。
(3)通过人工选择算子保存各种群每个进化代中的最优个体,并作为判断算法收敛的依据。
图7-1中,种群1~N的进化机制都是常规的SGA,采用轮盘赌选择、单点交叉和位点变异。
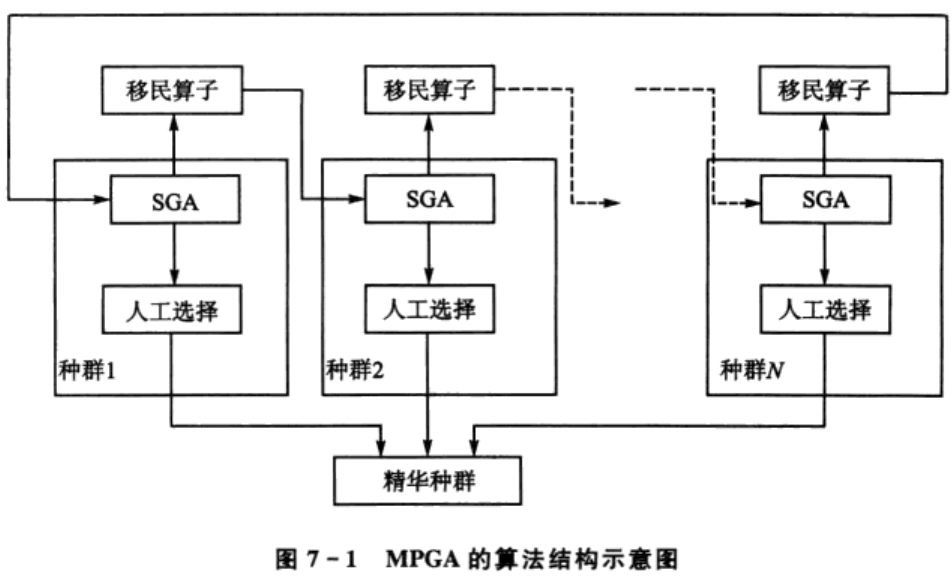
各种群取不同的控制参数。交叉概率Pe和变异概率Pm的取值决定了算法全局搜索和局部搜索能力的均衡。在SGA中,交叉算子是产生新个体的主要算子,它决定了遗传算法全局搜索的能力;而变异算子只是产生新个体的辅助算子,它决定了遗传算法的局部搜索能力。许多学者建议选择较大的Pe(0.7~0.9)和较小的Pm(0.001~0.05)。但是Pe和Pm的取值方式还是有无数种,对于不同的选择,优化结果差异也是很大的。MPGA弥补了SGA的这一不足,通过多个设有不同控制参数的种群协同进化,同时兼顾了算法的全局搜索和局部搜索。
各种群是相对独立的,相互之间通过移民算子联系。移民算子将各种群在进化过程中出现的最优个体定期地(每隔一定的进化代数)引入其他的种群中,实现种群之间的信息交换。具体的操作规则是,将目标种群中的最差个体用源种群的最优个体代替。移民算子在MPGA中至关重要,如果没有移民算子,各种群之间失去了联系,MPGA将等同于用不同的控制参数进行多次SGA计算,从而失去了MPGA的特色。
精华种群和其他种群有很大不同。在进化的每一代,通过人工选择算子选出其他种群的最优个体放入精华种群加以保存。精华种群不进行选择、交叉、变异等遗传操作,保证进化过程中各种群产生的最优个体不被破坏和丢失。同时,精华种群也是判断算法终止的依据,这里采用最优个体最少保持代数作为终止判据。这种判据充分利用了遗传算法在进化过程中的知识积累,较最大遗传代数判据更为合理。
2 案例背景
2.1 问题描述
复杂二元函数求最值:
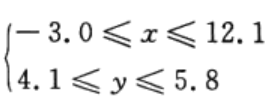
matlab代码及该函数的图形如下。
x = linspace(0, 12.1, 200);
y = linspace(4.1, 5.8, 200);
[x, y] = meshgrid(x,y);
f = 21.5+x.*sin(4*pi*x)+y.*sin(20*pi*y);
figure;
surf(x,y,f);
colormap(gca, 'jet')
xlabel('x');
ylabel('y');
zlabel('f(x,y)');
title('函数图像')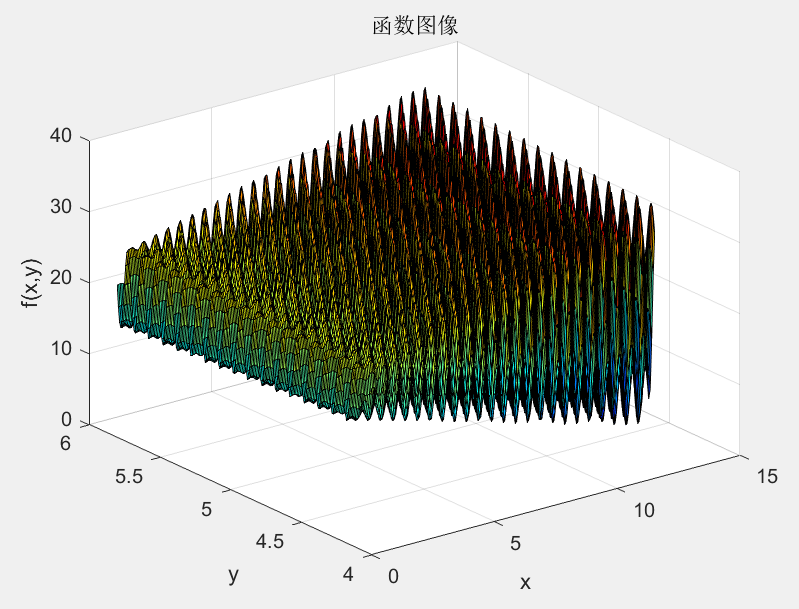
从图7-2中可以看出,该非线性函数在给定范围内分布着许多局部极值,通常的寻优算法极易陷入局部极值或在各局部极值间振荡,比较适用于验证多种群遗传算法的性能。
2.2 解题思路及步骤
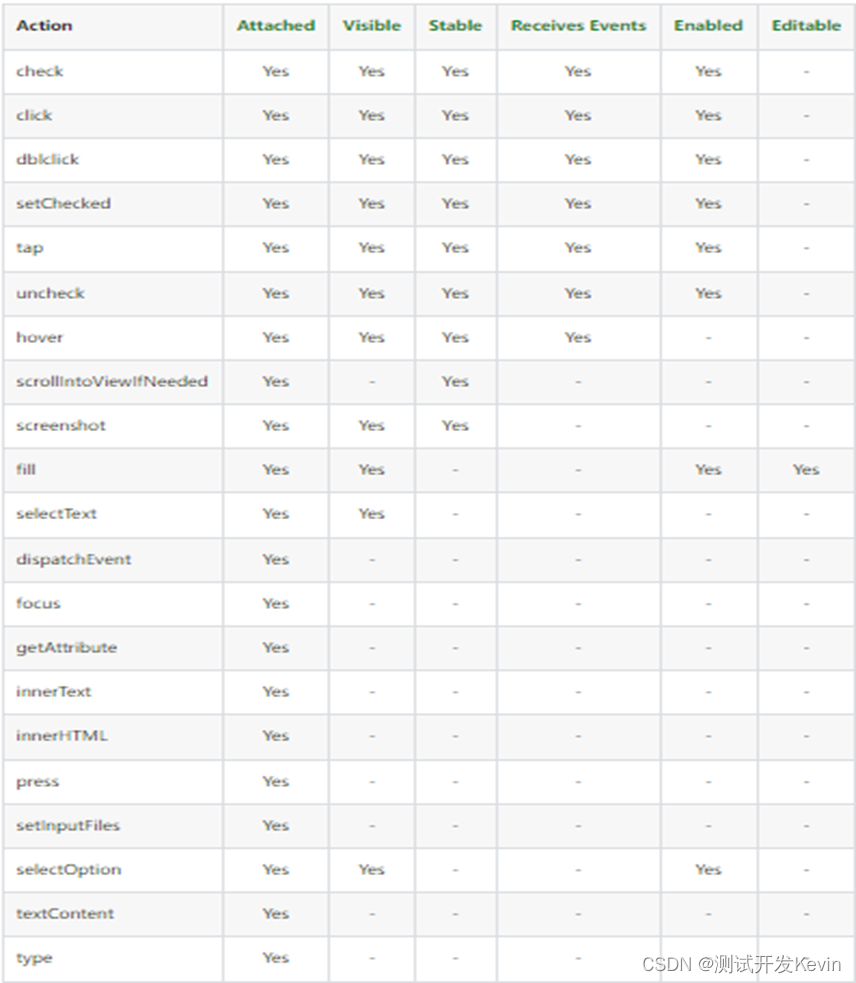
图7-1中的SGA流程图这里不再赘述。本例SGA部分使用英国谢菲尔德大学推出的基于MATLAB的遗传算法工具箱,具体的可以参考谢菲尔德大学的MATLAB遗传算法工具箱。本例使用到的工具箱函数如表7-1所列。
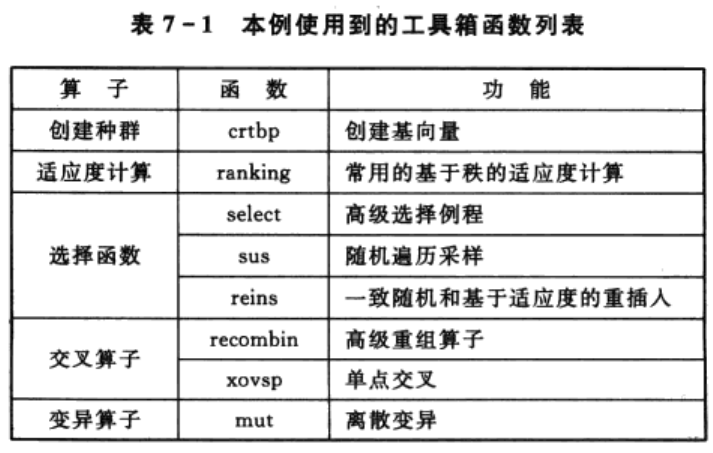
3 MATLAB程序实现
SGA部分直接使用英国谢菲尔德大学推出的基于MATLAB的遗传算法工具箱,所以对应的函数实现这里不做介绍,详细的可以参考工具箱函数。下面详细介绍移民算子和人工选择算子的实现。

3.1 移民算子
移民算子函数名为immigrant,函数的输入、输出参数如表7-2所列。

具体函数代码如下:
function [Chrom,ObjV]=immigrant(Chrom,ObjV)
%% 移民算子
MP=length(Chrom);
for i=1:MP
[MaxO,maxI]=max(ObjV{i}); % 找出第i种群中最优的个体
next_i=i+1; % 目标种群(移民操作中)
if next_i>MP;next_i=mod(next_i,MP);end
[MinO,minI]=min(ObjV{next_i}); % 找出目标种群中最劣的个体
%% 目标种群最劣个体替换为源种群最优个体
Chrom{next_i}(minI,:)=Chrom{i}(maxI,:);
ObjV{next_i}(minI)=ObjV{i}(maxI);
end
3.2 人工选择算子
人工选择算子函数名为EliteInduvidual,函数的输入、输出参数如表7-3所列。
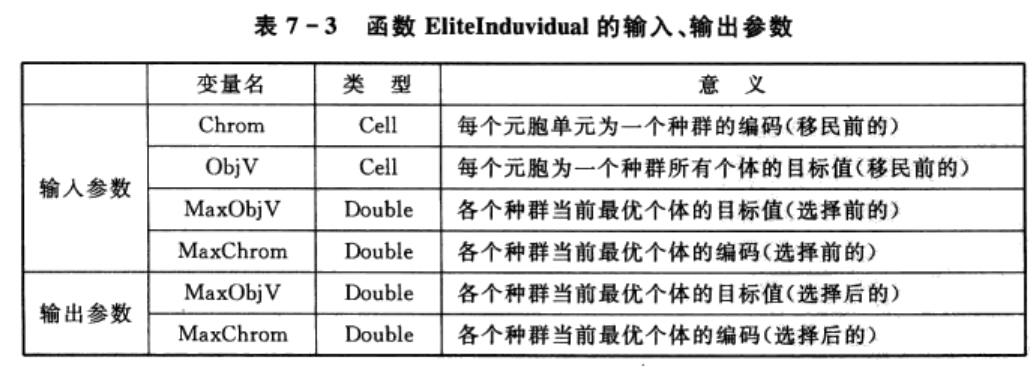
具体函数代码如下:
function [MaxObjV,MaxChrom]=EliteInduvidual(Chrom,ObjV,MaxObjV,MaxChrom)
%% 人工选择算子
MP=length(Chrom); %种群数
for i=1:MP
[MaxO,maxI]=max(ObjV{i}); %找出第i种群中最优个体
if MaxO>MaxObjV(i)
MaxObjV(i)=MaxO; %记录各种群的精华个体
MaxChrom(i,:)=Chrom{i}(maxI,:); %记录各种群精华个体的编码
end
end
3.3 目标函数
针对2.1节中提出的问题,写出目标函数,函数名为ObjectFunction。
function obj=ObjectFunction(X)
%% 待优化的目标函数
col=size(X,1);
for i=1:col
obj(i,1)=21.5+X(i,1)*sin(4*pi*X(i,1))+X(i,2)*sin(20*pi*X(i,2));
% obj(i,1)=exp(((X(i,1)-0.1)/0.8)^2)*(sin(5*pi*X(i,1)))^6;
end
3.4 标准遗传算法主函数
先使用标准遗传算法解决2.1节中的问题——复杂二元函数优化。实现的主函数代码如下:
%% 标准遗传算法SGA
clear;
%clc
pc=0.7; % 交叉概率
pm=0.05; % 变异概率
%定义遗传算法参数
NIND=40; %个体数目
MAXGEN=500; %最大遗传代数
NVAR=2; %变量的维数
PRECI=20; %变量的二进制位数
GGAP=0.9; %代沟
trace=zeros(MAXGEN,1); %记录优化轨迹
FieldD=[rep(PRECI,[1,NVAR]);[-3,4.1;12.1,5.8];rep([1;0;1;1],[1,NVAR])]; %建立区域描述器
Chrom=crtbp(NIND, NVAR*PRECI); %创建初始种群
gen=0; %代计数器
ObjV=ObjectFunction(bs2rv(Chrom, FieldD));%计算初始种群个体的目标函数值
[maxY,I]=max(ObjV); %最优值
X=bs2rv(Chrom, FieldD);
maxX=X(I,:);
while gen<MAXGEN %迭代
FitnV=ranking(-ObjV); %分配适应度值(Assign fitness values)
SelCh=select('sus', Chrom, FitnV, GGAP); %选择
SelCh=recombin('xovsp', SelCh, pc); %重组
SelCh=mut(SelCh,pm); %变异
ObjVSel=ObjectFunction(bs2rv(SelCh, FieldD)); %计算子代目标函数值
[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel); %重插入
gen=gen+1; %代计数器增加
if maxY<max(ObjV)
[maxY,I]=max(ObjV);
X=bs2rv(Chrom, FieldD);
maxX=X(I,:);
end
trace(gen,1)=maxY;
end
%% 进化过程图
plot(1:gen,trace(:,1));
hold on
xlabel('进化代数');
ylabel('最优解变化');
title('SGA进化过程');
%% 输出最优解
disp(['最优值为:',num2str(maxY)]);
disp(['对应的自变量取值:',num2str(maxX)]);
3.5 多种群遗传算法主函数
使用多种群遗传算法解决实现的主函数:
%%
%% 2、多种群遗传算法
clear;
clc
NIND=40; %个体数目
NVAR=2; %变量的维数
PRECI=20; %变量的二进制位数
GGAP=0.9; %代沟
MP=10; %种群数目
FieldD=[rep(PRECI,[1,NVAR]);[-3,4.1;12.1,5.8];rep([1;0;1;1],[1,NVAR])]; %译码矩阵
for i=1:MP
Chrom{i}=crtbp(NIND, NVAR*PRECI); %创建初始种群
end
pc=0.7+(0.9-0.7)*rand(MP,1); %在【0.7,0.9】范围i内随机产生交叉概率
pm=0.001+(0.05-0.001)*rand(MP,1); %在【0.001,0.05】范围内随机产生变异概率
gen=0; %初始遗传代数
gen0=0; %初始保持代数
MAXGEN=10; %最优个体最少保持代数
maxY=0; %最优值
for i=1:MP
ObjV{i}=ObjectFunction(bs2rv(Chrom{i}, FieldD));%计算各初始种群个体的目标函数值
end
MaxObjV=zeros(MP,1); %记录精华种群
MaxChrom=zeros(MP,PRECI*NVAR); %记录精华种群的编码
while gen0<=MAXGEN
gen=gen+1; %遗传代数加1
for i=1:MP
FitnV{i}=ranking(-ObjV{i}); % 各种群的适应度
SelCh{i}=select('sus', Chrom{i}, FitnV{i},GGAP); % 选择操作
SelCh{i}=recombin('xovsp',SelCh{i}, pc(i)); % 交叉操作
SelCh{i}=mut(SelCh{i},pm(i)); % 变异操作
ObjVSel=ObjectFunction(bs2rv(SelCh{i}, FieldD)); % 计算子代目标函数值
[Chrom{i},ObjV{i}]=reins(Chrom{i},SelCh{i},1,1,ObjV{i},ObjVSel); %重插入操作
end
[Chrom,ObjV]=immigrant(Chrom,ObjV); % 移民操作
[MaxObjV,MaxChrom]=EliteInduvidual(Chrom,ObjV,MaxObjV,MaxChrom); % 人工选择精华种群
YY(gen)=max(MaxObjV); %找出精华种群中最优的个体
if YY(gen)>maxY %判断当前优化值是否与前一次优化值相同
maxY=YY(gen); %更新最优值
gen0=0;
else
gen0=gen0+1; %最优值保持次数加1
end
end
%% 进化过程图
plot(1:gen,YY);
xlabel('进化代数')
ylabel('最优解变化')
title('MPGA进化过程')
%% 输出最优解
[Y,I]=max(MaxObjV); %找出精华种群中最优的个体
X=(bs2rv(MaxChrom(I,:), FieldD)); %最优个体的解码解
disp(['最优值为:',num2str(Y)])
disp(['对应的自变量取值:',num2str(X)])4 结果分析
标准遗传算法运行5次得到的结果如下所示。
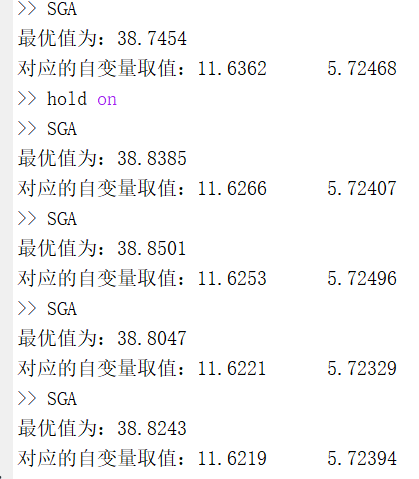
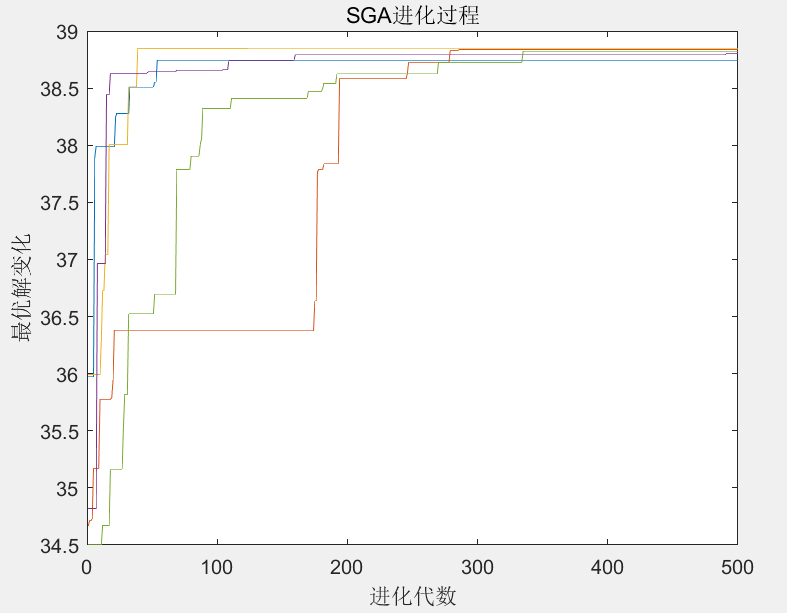
从结果可以看出,5次得到的优化结果均不相同,标准遗传算法很不稳定,而且在接近500代的时候仍然未稳定下来,说明最优解还有上升的可能。对于这种复杂的函数优化,使用标准的遗传算法已经很难得到最优解了。
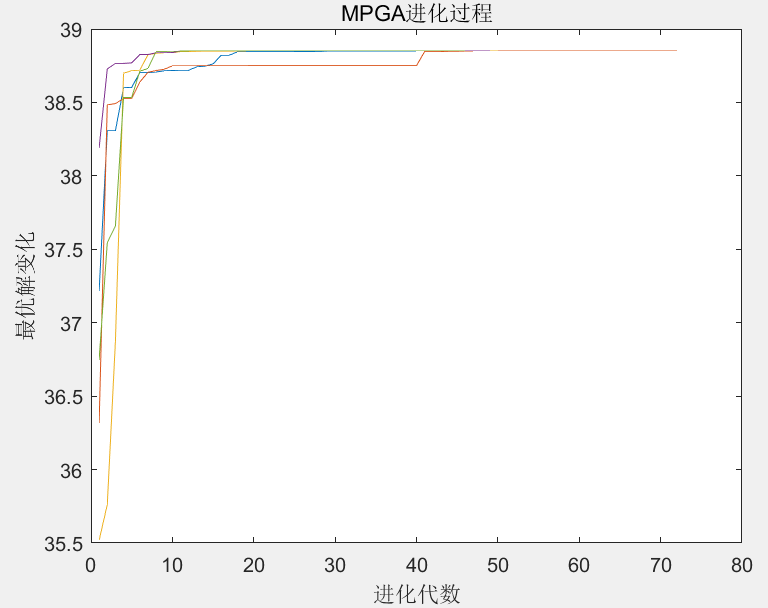

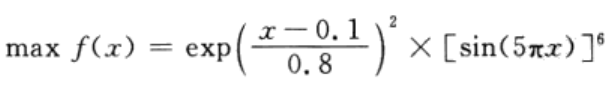
多种群遗传算法运行5次得到的结果如下。


从结果可以看出,多种群遗传算法运行5次的结果完全一致,说明多种群遗传算法稳定性很好,而且使用的遗传代数都很小,最大的不超过70代。可见,多种群遗传算法的收敛速度快,适合复杂问题的优化。因为MPGA中采用了多个种群同时对解空间进行协同搜索,兼顾了算法的全局搜索和局
部搜索,计算结果对遗传控制参数的敏感性大大降低,对克服未成熟收敛有显著的效果。
5 延伸阅读
在遗传算法的基础上,MPGA将SGA算法结构进行了扩展,引入了多个种群同时对解空间进行协同搜索,兼顾了算法全局搜索和局部搜索能力的均衡,大大降低了遗传控制参数的不当设定对规划结果的影响,对抑制未成熟收敛的发生有明显的效果。实际算例表明,MPGA用于复杂函数优化是非常有效的。 2.1节中的问题是对二元函数的优化,MPGA对于单元或者是其他任意元的函数优化均可以实现,只是需要稍微做些修改即可。例如在[0,1]区间求最大值:
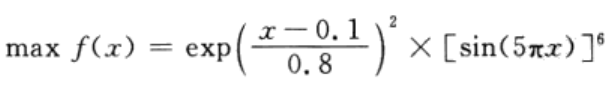
只需修改目标函数和主函数中变量的维数和译码矩阵即可。