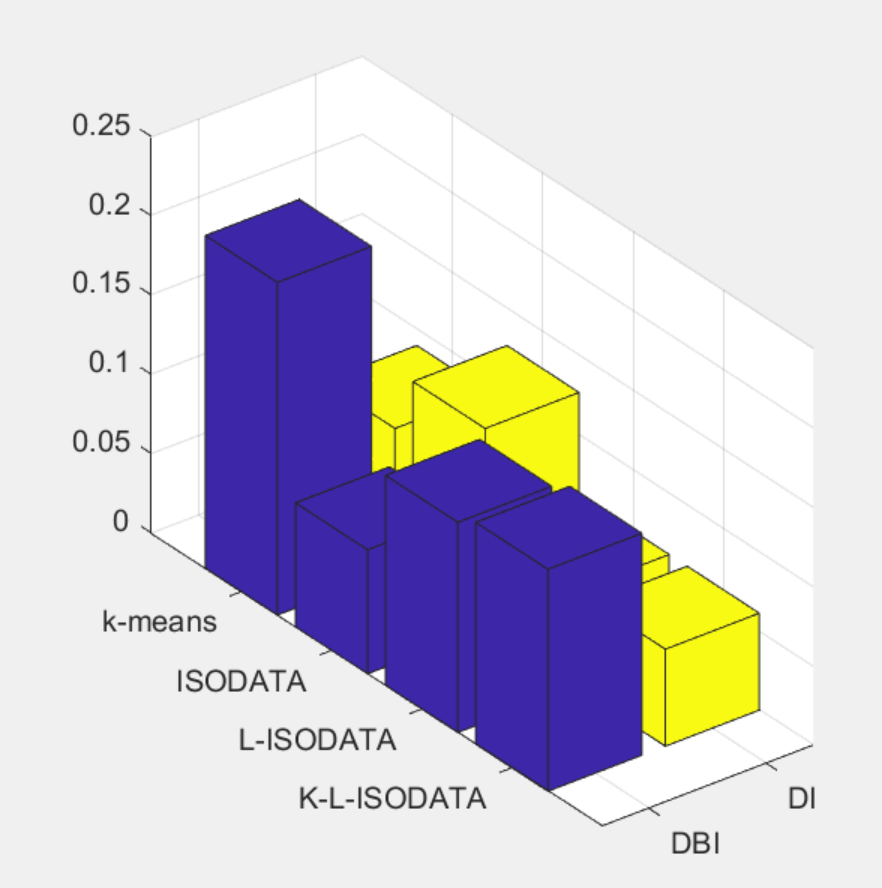
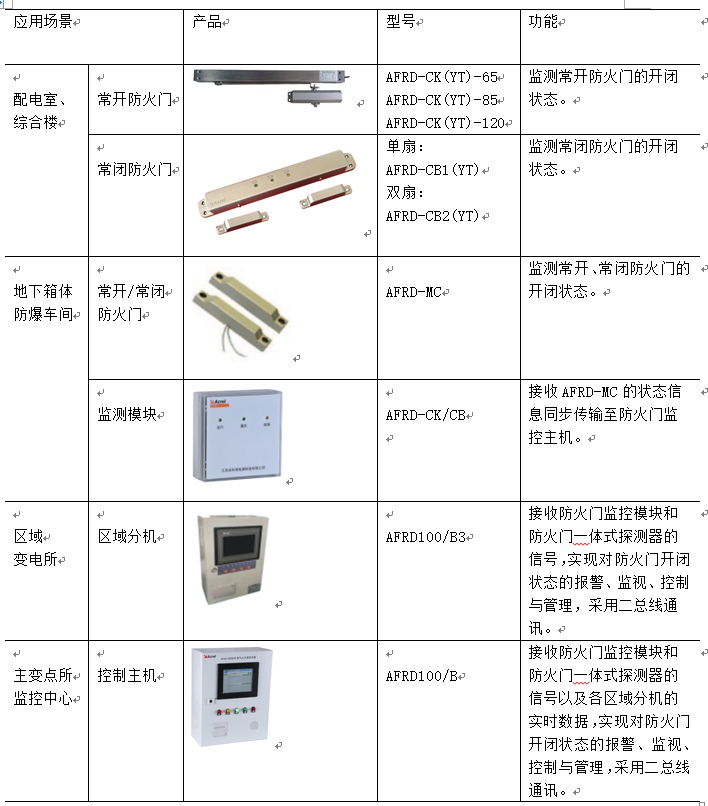
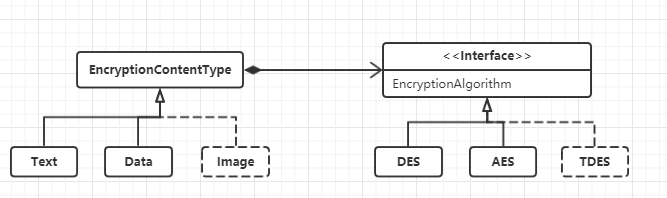
商代数
设
R
R
R使
A
=
<
S
,
∗
1
,
∗
2
,
⋯
,
∗
n
>
A = \left<S, *_1, *_2,\cdots, *_n\right>
A=⟨S,∗1,∗2,⋯,∗n⟩上的同余关系,则
R
R
R使
S
S
S上的等价关系,因此
R
R
R可诱导出
S
S
S的一个划分
S
/
R
=
{
[
a
]
R
∣
a
∈
S
}
S/ R = \left\{\left[a\right]_R | a \in S\right\}
S/R={[a]R∣a∈S}.对于运算
∗
i
*_i
∗i,定义
S
/
R
S/R
S/R上的同阶运算
⊛
i
\circledast_i
⊛i为:
∀
[
a
1
]
R
,
[
a
2
]
R
,
⋯
,
[
a
n
i
]
R
∈
S
/
R
\forall \left[a_1\right]_R, \left[a_2\right]_R,\cdots, \left[a_{n_i}\right]_R \in S / R
∀[a1]R,[a2]R,⋯,[ani]R∈S/R,
⊛
i
(
[
a
1
]
R
,
[
a
2
]
R
,
⋯
,
[
a
n
i
]
R
)
=
[
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
]
R
\circledast_i\left(\left[a_1\right]_R,\left[a_2\right]_R, \cdots,\left[a_{n_i}\right]_R\right) = \left[*_i\left(a_1,a_2,\cdots, a_{n_i}\right)\right]_R
⊛i([a1]R,[a2]R,⋯,[ani]R)=[∗i(a1,a2,⋯,ani)]R
⊛
i
\circledast_i
⊛i是良定的,因为运算结果并不依赖于各等价类的代表元的选取:
若
[
a
k
]
R
=
[
b
k
]
R
\left[a_k\right]_R = \left[b_k\right]_R
[ak]R=[bk]R, 则
a
k
R
b
k
a_k R b_k
akRbk,因为
R
R
R是
A
A
A上的同余关系,所以
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
R
∗
i
(
b
1
,
b
2
,
⋯
,
b
n
i
)
*_i\left(a_1,a_2,\cdots, a_{n_i}\right) R *_i\left(b_1,b_2,\cdots, b_{n_i}\right)
∗i(a1,a2,⋯,ani)R∗i(b1,b2,⋯,bni),故
[
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
]
R
=
[
∗
i
(
b
1
,
b
2
,
⋯
,
b
n
i
)
]
R
\left[*_i\left(a_1,a_2,\cdots, a_{n_i}\right)\right]_R = \left[*_i\left(b_1,b_2,\cdots, b_{n_i}\right)\right]_R
[∗i(a1,a2,⋯,ani)]R=[∗i(b1,b2,⋯,bni)]R
设
R
R
R是代数系统
A
=
<
S
,
∗
1
,
∗
2
,
⋯
,
∗
n
>
A=\left<S, *_1, *_2,\cdots, *_n\right>
A=⟨S,∗1,∗2,⋯,∗n⟩删的同余关系,则称代数系统
A
/
R
=
<
S
/
R
,
⊛
1
,
⊛
2
,
⋯
,
⊛
n
>
A/R = \left<S/R, \circledast_1,\circledast_2,\cdots, \circledast_n\right>
A/R=⟨S/R,⊛1,⊛2,⋯,⊛n⟩为
A
A
A关于
R
R
R的商代数
定理1: 设
R
R
R是代数系统
A
=
<
S
,
∗
1
,
∗
2
,
⋯
,
∗
n
>
A = \left<S, *_1, *_2,\cdots, *_n\right>
A=⟨S,∗1,∗2,⋯,∗n⟩上的同余关系,函数
f
:
S
→
S
/
R
f:S\to S/R
f:S→S/R定义为
∀
a
∈
S
,
f
(
a
)
=
[
a
]
R
\forall a \in S, f\left(a\right) = \left[a\right]_R
∀a∈S,f(a)=[a]R,则
f
f
f是从
A
A
A到商代数
A
/
R
A/R
A/R的满同态,称为自然同态
证明:
∀
i
∈
N
(
1
≤
i
≤
n
)
,
∀
a
1
,
a
2
,
⋯
,
a
n
i
∈
S
\forall i \in \mathbb{N}\left(1\le i \le n\right), \forall a_1, a_2,\cdots, a_{n_i} \in S
∀i∈N(1≤i≤n),∀a1,a2,⋯,ani∈S
f
(
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
)
=
[
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
]
R
=
⊛
i
(
[
a
1
]
R
,
[
a
2
]
R
,
⋯
,
[
a
n
i
]
R
)
=
⊛
i
(
f
(
a
1
)
,
f
(
a
2
)
,
⋯
,
f
(
a
n
i
)
)
\begin{aligned} f\left(*_i\left(a_1,a_2,\cdots, a_{n_i}\right)\right) &= \left[*_i\left(a_1,a_2,\cdots, a_{n_i}\right)\right]_R\\ &=\circledast_i\left(\left[a_1\right]_R,\left[a_2\right]_R, \cdots,\left[a_{n_i}\right]_R\right)\\ &=\circledast_i\left(f\left(a_1\right),f\left(a_2\right), \cdots,f\left(a_{n_i}\right)\right) \end{aligned}
f(∗i(a1,a2,⋯,ani))=[∗i(a1,a2,⋯,ani)]R=⊛i([a1]R,[a2]R,⋯,[ani]R)=⊛i(f(a1),f(a2),⋯,f(ani))
所以
f
f
f为
A
A
A到
A
/
R
A/R
A/R的同态。
又
∀
x
∈
S
/
R
,
∃
a
∈
S
\forall x \in S/R,\exists a \in S
∀x∈S/R,∃a∈S,使得
x
=
[
a
]
R
x = \left[a\right]_R
x=[a]R,于是
f
(
a
)
=
[
a
]
R
=
x
f\left(a\right) = \left[a\right]_R = x
f(a)=[a]R=x,所以
f
f
f满射。故
f
f
f为
A
A
A到
A
/
R
A/R
A/R的满同态
由于
f
f
f是从
A
A
A到
A
/
R
A/R
A/R的满同态,因此
A
A
A的主要代数性质再其商代数
A
/
R
A/R
A/R中仍然保持
定理2: 设
h
h
h是从
A
=
<
S
,
∗
1
,
∗
2
,
⋯
,
∗
n
>
A=\left<S, *_1, *_2,\cdots, *_n\right>
A=⟨S,∗1,∗2,⋯,∗n⟩到
A
′
=
<
S
′
,
∗
1
′
,
∗
2
′
,
⋯
,
∗
n
′
>
A^{\prime}=\left<S^{\prime}, *_1^{\prime}, *_2^{\prime},\cdots, *_n^{\prime}\right>
A′=⟨S′,∗1′,∗2′,⋯,∗n′⟩的同态
R
R
R是
A
A
A上由
h
h
h诱导的同余关系,
f
f
f是从
A
A
A到商代数
A
/
R
A/R
A/R的自然同态,那么存在从
A
/
R
A/R
A/R到
h
(
A
)
h\left(A\right)
h(A)的同构
g
g
g,使得
g
∘
f
=
h
g\circ f = h
g∘f=h
证明:
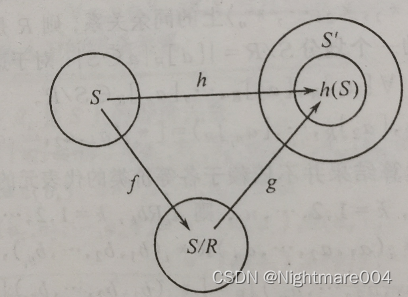
作
g
:
S
/
R
→
h
(
S
)
,
[
a
]
R
↦
h
(
a
)
g:S/R \to h\left(S\right), [a]_R \mapsto h(a)
g:S/R→h(S),[a]R↦h(a)
1.
g
g
g是良定的,
∀
[
a
]
R
,
[
b
]
R
∈
S
/
R
\forall \left[a\right]_R, \left[b\right]_R \in S / R
∀[a]R,[b]R∈S/R,若
[
a
]
R
=
[
b
]
R
\left[a\right]_R = \left[b\right]_R
[a]R=[b]R,则
a
R
b
aRb
aRb,所以
h
(
a
)
=
h
(
b
)
h\left(a\right) = h\left(b\right)
h(a)=h(b)
2.
g
g
g是单射。
∀
[
a
]
R
,
[
b
]
R
∈
S
/
R
\forall \left[a\right]_R, \left[b\right]_R\in S/R
∀[a]R,[b]R∈S/R,若
g
(
[
a
]
R
)
=
g
(
[
b
]
R
)
g\left(\left[a\right]_R\right) = g\left(\left[b\right]_R\right)
g([a]R)=g([b]R),则
h
(
a
)
=
h
(
b
)
h\left(a\right) = h\left(b\right)
h(a)=h(b),所以
a
R
b
,
[
a
]
R
=
[
b
]
R
aRb, \left[a\right]_R= \left[b\right]_R
aRb,[a]R=[b]R
3.
g
g
g是满射,
∀
x
∈
h
(
S
)
,
∃
a
∈
S
\forall x \in h\left(S\right),\exists a \in S
∀x∈h(S),∃a∈S,使得
h
(
a
)
=
x
h\left(a\right) = x
h(a)=x,所以
g
(
[
a
]
R
)
=
h
(
a
)
=
x
g\left(\left[a\right]_R\right) = h\left(a\right) = x
g([a]R)=h(a)=x
4.
g
g
g是同态,
∀
i
∈
N
(
1
≤
i
≤
n
)
,
∀
[
a
1
]
R
,
[
a
2
]
R
,
⋯
,
[
a
n
i
]
R
∈
S
/
R
\forall i \in \mathbb{N}\left(1\le i \le n\right) ,\forall \left[a_1\right]_R,\left[a_2\right]_R,\cdots, \left[a_{n_i}\right]_R \in S/ R
∀i∈N(1≤i≤n),∀[a1]R,[a2]R,⋯,[ani]R∈S/R
g
(
⊛
i
(
[
a
1
]
R
,
[
a
2
]
R
,
⋯
,
[
a
n
i
]
R
)
)
=
g
(
[
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
]
R
)
=
h
(
∗
i
(
a
1
,
a
2
,
⋯
,
a
n
i
)
)
=
∗
i
′
(
h
(
a
1
)
,
h
(
a
2
)
,
⋯
,
h
(
a
n
i
)
)
=
∗
i
′
(
g
(
[
a
1
]
R
)
,
g
(
[
a
2
]
R
)
,
⋯
,
g
(
[
a
n
i
]
R
)
)
\begin{aligned} &g\left(\circledast_i\left(\left[a_1\right]_R,\left[a_2\right]_R,\cdots, \left[a_{n_i}\right]_R\right)\right)\\ =&g\left(\left[*_i\left(a_1,a_2,\cdots, a_{n_i}\right)\right]_R\right)\\ =&h\left(*_i\left(a_1,a_2,\cdots, a_{n_i}\right)\right)\\ =&*_i^{\prime}\left(h\left(a_1\right), h\left(a_2\right),\cdots, h\left(a_{n_i}\right)\right)\\ =&*_i^{\prime}\left(g\left(\left[a_1\right]_R\right), g\left(\left[a_2\right]_R\right), \cdots, g\left(\left[a_{n_i}\right]_R\right)\right) \end{aligned}
====g(⊛i([a1]R,[a2]R,⋯,[ani]R))g([∗i(a1,a2,⋯,ani)]R)h(∗i(a1,a2,⋯,ani))∗i′(h(a1),h(a2),⋯,h(ani))∗i′(g([a1]R),g([a2]R),⋯,g([ani]R))
故
g
g
g是从
A
/
R
A/R
A/R到
h
(
A
)
h\left(A\right)
h(A)的同构
并且
∀
a
∈
S
,
g
∘
f
(
a
)
=
g
(
f
(
a
)
)
=
g
(
[
a
]
R
)
=
h
(
a
)
\forall a \in S, g\circ f\left(a\right) = g\left(f\left(a\right)\right) = g\left(\left[a\right]_R\right) = h\left(a\right)
∀a∈S,g∘f(a)=g(f(a))=g([a]R)=h(a),故
g
∘
f
=
h
g\circ f = h
g∘f=h
推论:设
h
h
h是从
A
A
A到
A
′
A^{\prime}
A′的满同态,
R
R
R是
A
A
A上由
h
h
h诱导的同余关系,则
A
/
R
≅
A
′
A/R \cong A^{\prime}
A/R≅A′
积代数
设
A
i
=
<
S
i
,
∗
i
1
,
∗
i
2
,
⋯
,
∗
i
n
>
(
i
=
1
,
2
,
⋯
,
m
)
A_i=\left<S_i, *_{i1}, *_{i2},\cdots, *_{in}\right>\left(i=1,2,\cdots, m\right)
Ai=⟨Si,∗i1,∗i2,⋯,∗in⟩(i=1,2,⋯,m)为同型的代数系统,
则
A
1
,
A
2
,
⋯
,
A
m
A_1,A_2,\cdots, A_m
A1,A2,⋯,Am的积代数
×
i
=
1
m
A
i
\times_{i=1}^{m}A_i
×i=1mAi定义为代数系统
<
×
i
=
1
m
S
i
,
∗
1
,
∗
2
,
⋯
,
∗
n
>
\left<\times_{i=1}^{m} S_i,*_1,*_2,\cdots, *_n\right>
⟨×i=1mSi,∗1,∗2,⋯,∗n⟩,其中运算
∗
j
*_j
∗j定义如下:
∀
<
a
11
,
a
21
,
⋯
,
a
m
1
>
,
<
a
12
,
a
22
,
⋯
,
a
m
2
>
,
⋯
<
a
1
n
j
,
a
2
n
j
,
⋯
,
a
m
n
j
>
∈
S
1
×
S
2
×
⋯
×
S
m
\forall \left<a_{11}, a_{21},\cdots, a_{m1}\right>, \left<a_{12}, a_{22},\cdots, a_{m2}\right>,\cdots \left<a_{1n_{j}}, a_{2n_{j}},\cdots, a_{mn_{j}}\right>\in S1\times S_2\times \cdots \times S_m
∀⟨a11,a21,⋯,am1⟩,⟨a12,a22,⋯,am2⟩,⋯⟨a1nj,a2nj,⋯,amnj⟩∈S1×S2×⋯×Sm,
∗
j
(
⟨
a
11
,
a
21
,
⋯
,
a
m
1
⟩
,
⟨
a
12
,
a
22
,
⋯
,
a
m
2
⟩
,
⋯
,
⟨
a
1
n
j
,
a
2
n
j
,
⋯
,
a
m
n
j
⟩
)
=
⟨
∗
1
j
(
a
11
,
a
12
,
⋯
,
a
1
n
j
)
,
∗
2
j
(
a
21
,
a
22
,
⋯
,
a
2
n
j
)
,
⋯
,
∗
m
j
(
a
m
1
,
a
m
2
,
⋯
,
a
m
n
j
)
⟩
.
\begin{aligned} & *_j\left(\left\langle a_{11}, a_{21}, \cdots, a_{m 1}\right\rangle,\left\langle a_{12}, a_{22}, \cdots, a_{m 2}\right\rangle, \cdots,\left\langle a_{1 n_j}, a_{2 n_j}, \cdots, a_{m n_j}\right\rangle\right) \\ & =\left\langle *_{1 j}\left(a_{11}, a_{12}, \cdots, a_{1 n_j}\right), *_{2 j}\left(a_{21}, a_{22}, \cdots, a_{2 n_j}\right), \cdots,\right. \\ & \left.\quad *{ }_{m j}\left(a_{m 1}, a_{m 2}, \cdots, a_{m n_j}\right)\right\rangle . \end{aligned}
∗j(⟨a11,a21,⋯,am1⟩,⟨a12,a22,⋯,am2⟩,⋯,⟨a1nj,a2nj,⋯,amnj⟩)=⟨∗1j(a11,a12,⋯,a1nj),∗2j(a21,a22,⋯,a2nj),⋯,∗mj(am1,am2,⋯,amnj)⟩.
定理: 设 A i = < S i , ∗ i , + i > A_i = \left<S_i, *_i, +_i\right> Ai=⟨Si,∗i,+i⟩为同型的代数系统, ∗ i *_i ∗i和 + i +_i +i为二元运算,积代数 × i = 1 m A i = < × i = 1 m S i , ∗ , + > \times_{i=1}^{m}A_i=\left<\times_{i=1}^{m}S_i, *, +\right> ×i=1mAi=⟨×i=1mSi,∗,+⟩
(1)若
∗
i
*_i
∗i可交换,则
∗
*
∗也是可交换的
(2)若
∗
i
*_i
∗i是可结合的,则
∗
*
∗也是可结合的
(3)若
∗
i
*_i
∗i关于
+
i
+_i
+i是可分配的,则
∗
*
∗关于
+
+
+也是可分配的
(4)若
e
i
e_i
ei是关于
∗
i
*_i
∗i的单位元,则
<
e
1
,
e
2
,
⋯
,
e
m
>
\left<e_1,e_2,\cdots, e_m\right>
⟨e1,e2,⋯,em⟩是关于
∗
*
∗的单位元
(5)若
0
i
0_i
0i是关于
∗
i
*_i
∗i的零元,则
<
0
1
,
0
2
,
⋯
,
0
m
>
\left<0_1,0_2,\cdots, 0_m\right>
⟨01,02,⋯,0m⟩是关于
∗
*
∗的零元
(6)若
a
i
∈
S
i
a_i\in S_i
ai∈Si关于
∗
i
*_i
∗i由逆元
a
−
1
a^{-1}
a−1,则
<
a
1
,
a
2
,
⋯
,
a
m
>
\left<a_1,a_2,\cdots, a_m\right>
⟨a1,a2,⋯,am⟩关于
∗
*
∗由逆元
<
a
1
−
1
,
a
2
−
1
,
⋯
,
a
m
−
1
>
\left<a_1^{-1},a_2^{-1},\cdots, a_m^{-1}\right>
⟨a1−1,a2−1,⋯,am−1⟩