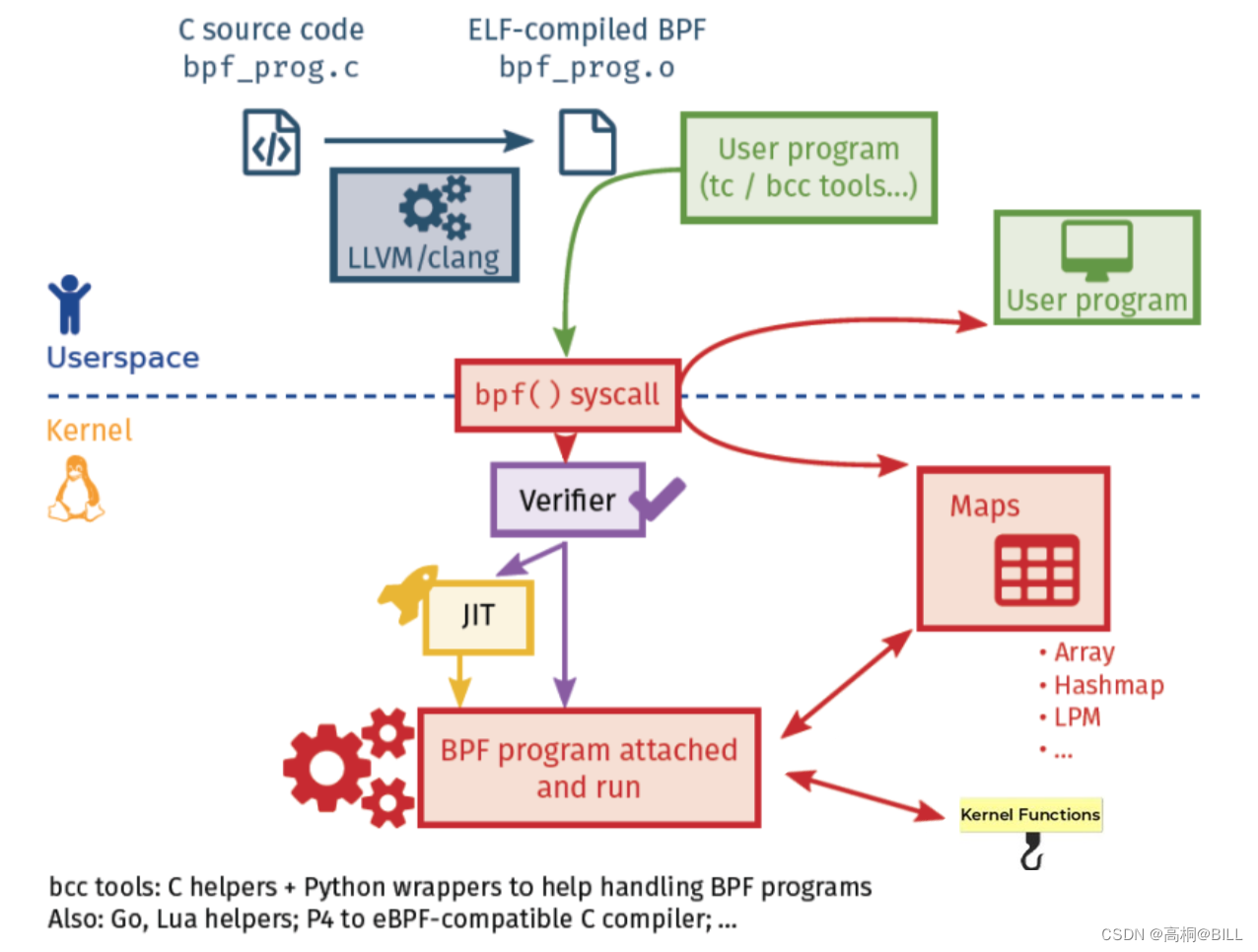
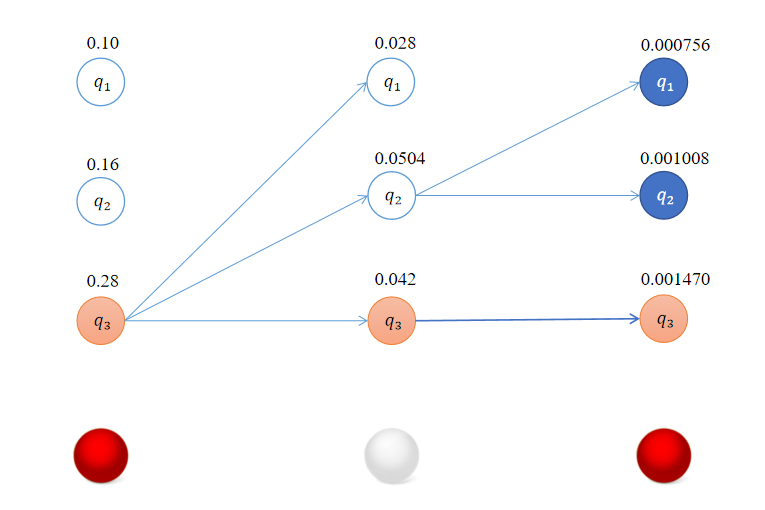
如果 w 和 z 的变换是线性的，即 w = az + b，那么 dw = a dz，

所以 p(w) dw = p(z) dz 等价于 p(w) a = p(z)

即 w 的概率密度函数是 z 的概率密度函数乘以一个常数因子。

如果 w 和 z 是通过一个可逆的函数 ϕ 相互转换的，即 w = ϕ(z) 和 z = ϕ -1 (w)，

那么 w 和 z 的概率密度函数 p(w) 和 p(z) 之间有如下关系：p(w) dw = p(z) dz，其中 dw 和 dz 是微元。

对上式两边取对数，得到 log p(w) + log dw = log p(z) + log dz。

由于 dw = |det ∂ϕ/∂z| dz，其中 ∂ϕ/∂z 是雅可比矩阵，det 是行列式，

在线性变换中，|det ∂ϕ/∂z|是**雅可比行列式**，它表示了函数 ϕ 在 z 处的**局部线性近似**对面积或体积的**放缩因子**。¹ 如果 |det ∂ϕ/∂z| 大于 1，那么函数 ϕ 会使得 z 附近的区域扩大；如果 |det ∂ϕ/∂z| 小于 1，那么函数 ϕ 会使得 z 附近的区域缩小；如果 |det ∂ϕ/∂z| 等于 0，那么函数 ϕ 会使得 z 附近的区域退化为一条线或一个点。

log p(w) = log p(z) + log dz - log dw

把 log dw = log |det ∂ϕ/∂z| + log dz代入上式，得到

log p(w) = log p(z) + log dz  -  log |det ∂ϕ/∂z|  - log dz

得到 log p(w) = log p(z) - log |det ∂ϕ/∂z|。如果 w 的概率密度函数是由属性特征 a t 条件化的，即 p(w |a t )，那么上式仍然成立，只是要加上条件 a t ，即 p(w |a t ) = p(z) |det ∂ϕ/∂z|。¹

 log p(w |a t ) = log p(z) - log |det ∂ϕ/∂z|

 -------------------------------------------------------------

Discrete Normalizing Flows

 

 

 

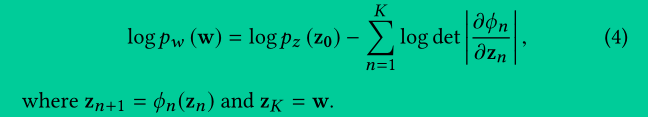
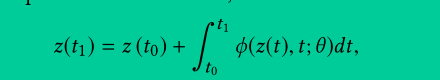
这个公式的含义是：变量 z 在时间 t1 的值，等于变量 z 在时间 t0 的值，加上从时间 t0 到时间 t1 之间变量 z 的变化量的积分。变量 z 的变化量由函数 ϕ 决定，函数 ϕ 取决于变量 z 、时间 t 和神经网络的参数 θ 。这个公式可以用来求解常微分方程 dz dt = ϕ(z(t),t;θ) ，也就是 CNFs 的变换函数。 

变量 z 在时间 t1 的概率密度的对数，等于变量 z 在时间 t0 的概率密度的对数，减去从时间 t0 到时间 t1 之间，函数 ϕ 对变量 z 的偏导数矩阵的迹的积分。函数 ϕ 对变量 z 的偏导数矩阵是雅克比矩阵，其迹是对角线元素之和。这个公式可以用来计算 CNFs 的变换后的概率密度和对数似然。

其中Tr（***/***）所代表的含义：

函数 ϕ 对变量 z 的偏导数矩阵的迹，即矩阵的对角线元素之和。函数 ϕ 对变量 z 的偏导数矩阵是雅克比矩阵，雅克比矩阵的迹表示变量 z 的总变化率。

这段文字是论文中介绍连续正则化流（Continuous Normalizing Flows，CNFs）的部分。它首先介绍了CNFs的数学原理，即使用常微分方程（Ordinary Differential Equations，ODEs）来表示变量之间的可逆变换，以及如何计算变换后的概率密度和对数似然。然后它解释了为什么选择CNFs而不是离散正则化流（Discrete Normalizing Flows，DNFs），主要有三个原因：一是CNFs保证了可逆性，而DNFs需要满足一些条件；二是CNFs的雅克比行列式更容易计算，而DNFs需要计算行列式；三是CNFs可以学习更解耦的内部表示，而DNFs可能存在一些耦合。最后，它说明了在StyleFlow框架中，如何使用CNFs来进行基于属性的采样和编辑。