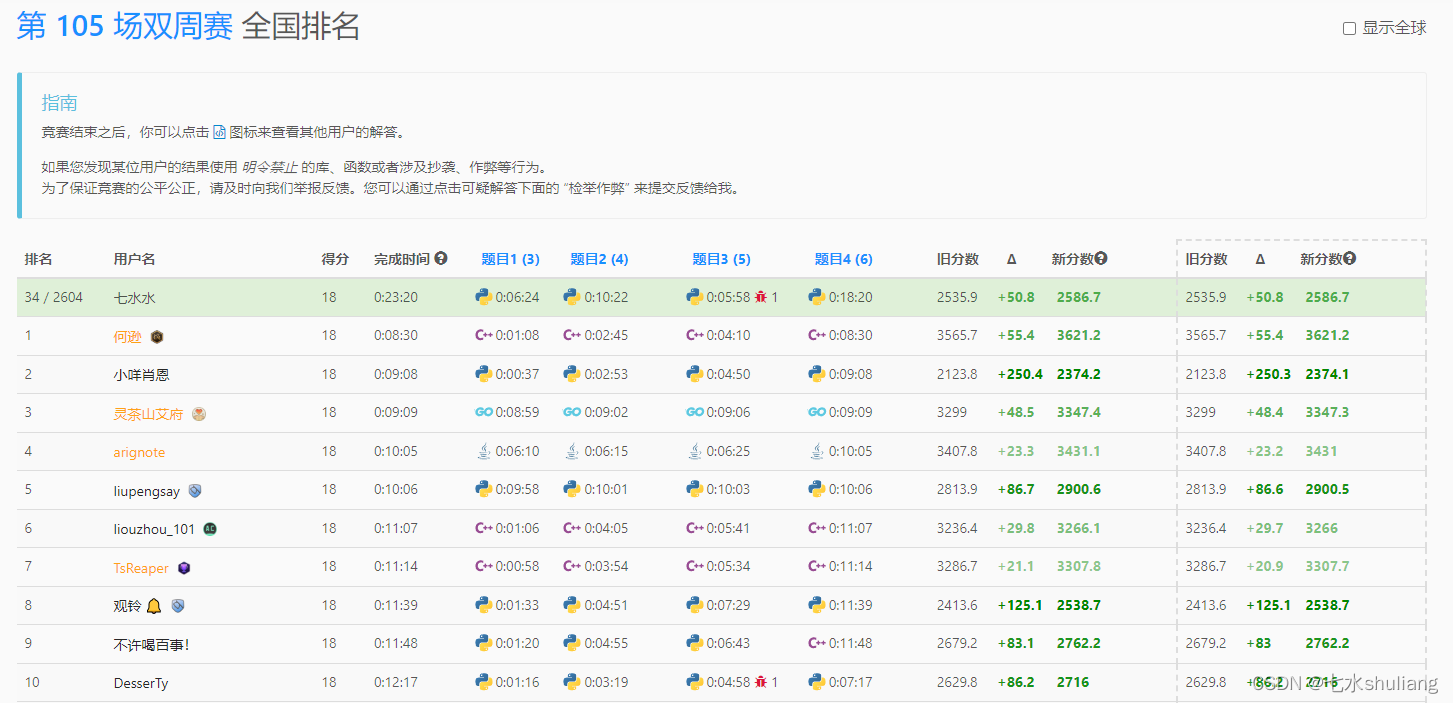
[LeetCode周赛复盘] 第 105 场双周赛20230528
- 一、本周周赛总结
- 6395. 购买两块巧克力
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 6394. 字符串中的额外字符
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 6393. 一个小组的最大实力值
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
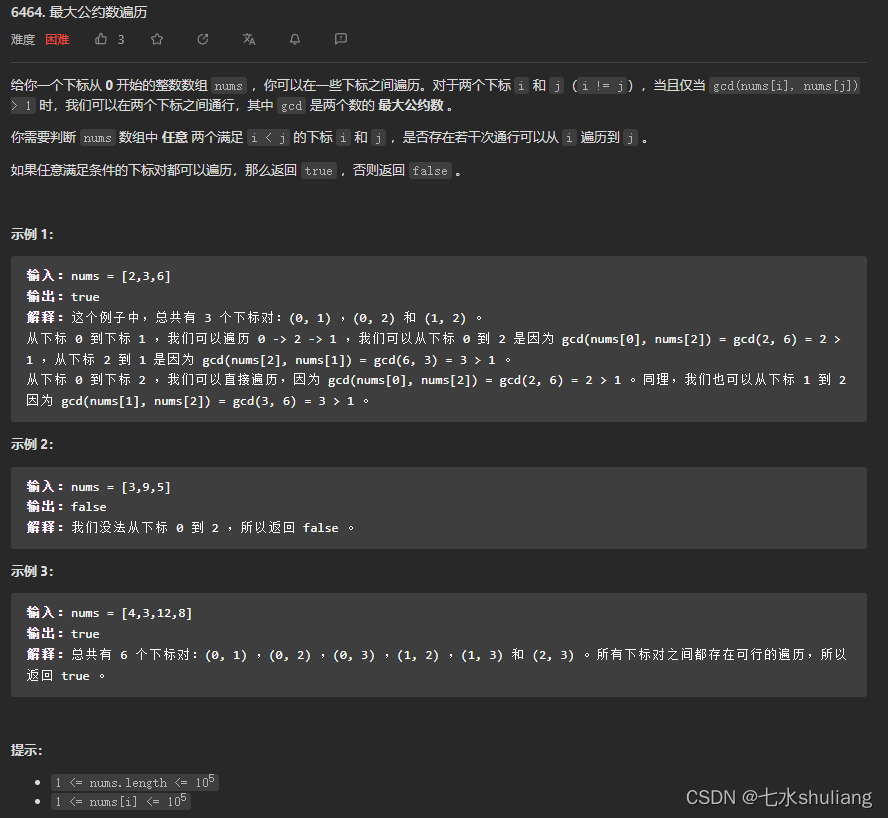
- 6464. 最大公约数遍历
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- 史上发挥最好的一次了,可惜T3空集wa了一次。
- T1 贪心。
- T2 dp。
- T3 状压/dfs/dp。
- T4 分解质因数+并查集。
6395. 购买两块巧克力
6395. 购买两块巧克力
1. 题目描述
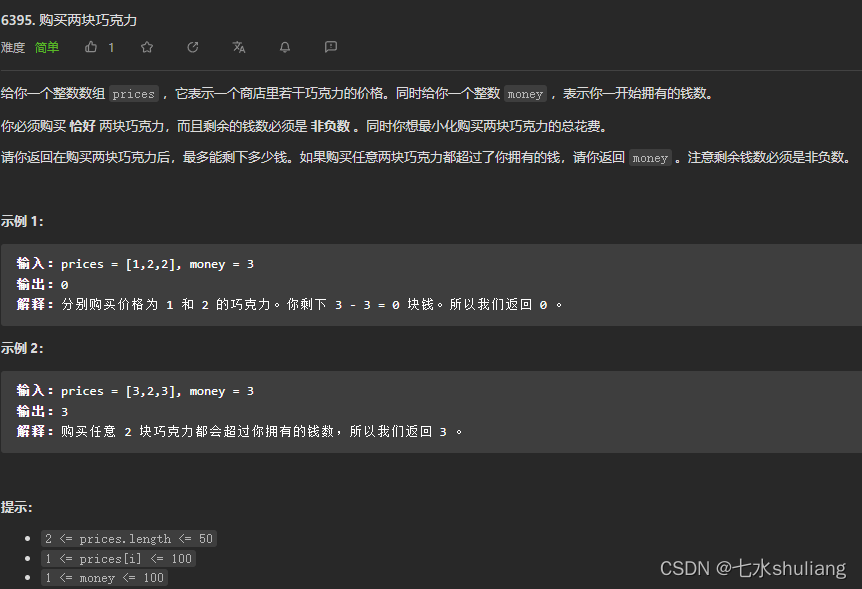
2. 思路分析
- 贪心的取最便宜的两块。
3. 代码实现
class Solution:
def buyChoco(self, prices: List[int], money: int) -> int:
prices.sort()
ans = money - sum(prices[:2])
return ans if ans >= 0 else money
6394. 字符串中的额外字符
6394. 字符串中的额外字符
1. 题目描述
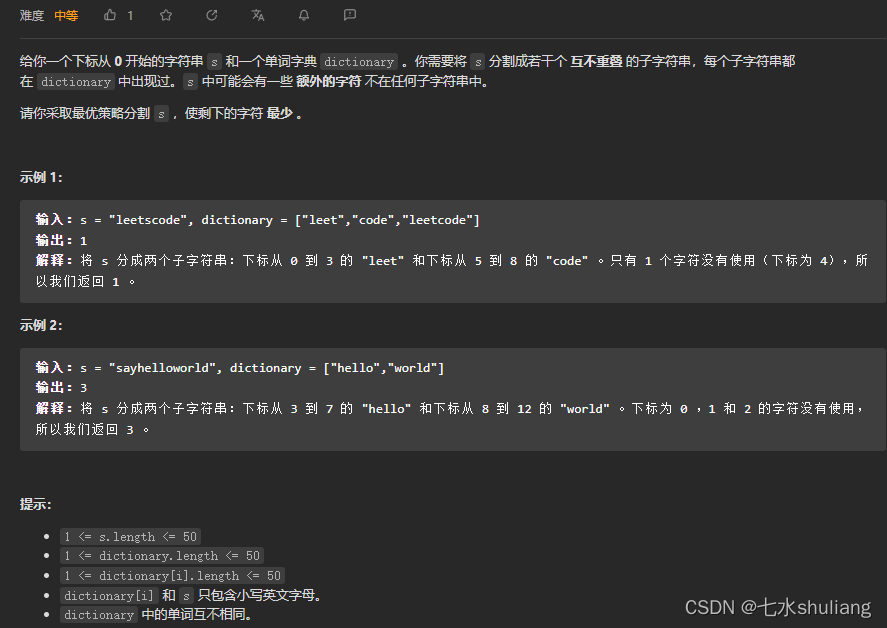
2. 思路分析
dp
- 由于是分割子串,那么讨论最后一段的长度即可。
- 令f[i]为前i个人字符最少剩下的字符。
- 若后缀s[j…i]在字典里,则f[i]=f[j-1]。
- 另外f[i]最差=f[i-1]+1。
- 实现时令下标右移一位方便处理。
- 另外可以用trie优化成n方。
3. 代码实现
class Solution:
def minExtraChar(self, s: str, dictionary: List[str]) -> int:
n = len(s)
dc = set(dictionary)
f = [0]+[inf]*n
for i in range(n):
f[i+1] = f[i]+1
for j in range(i,-1,-1):
if s[j:i+1] in dc:
f[i+1] = min(f[i+1], f[j])
return f[-1]
6393. 一个小组的最大实力值
6393. 一个小组的最大实力值
1. 题目描述
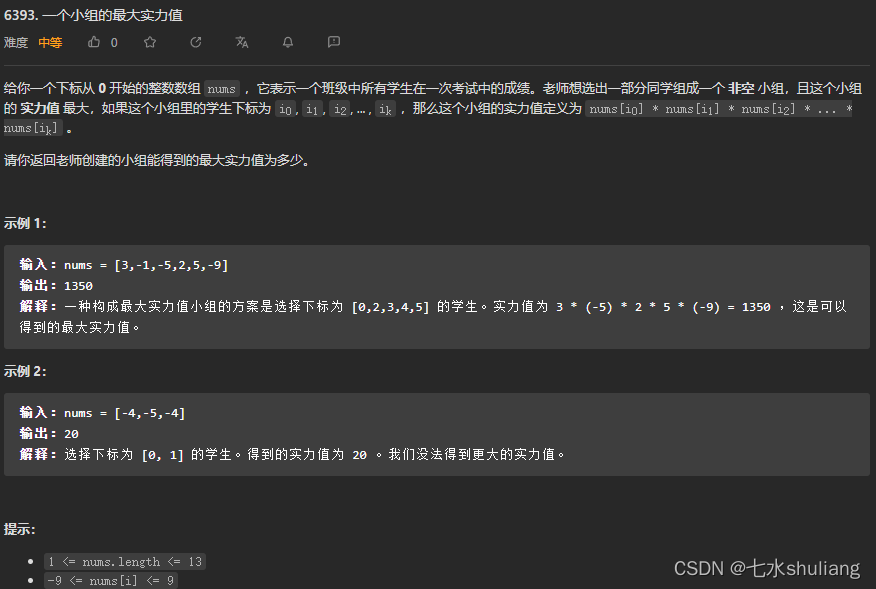
2. 思路分析
- 看到数据量立刻就想暴力。
- 之前有一道数据量20的状压会被卡,这次不会了。
- 当然最优解是dp或者贪心。
3. 代码实现
class Solution:
def maxStrength(self, nums: List[int]) -> int:
n = len(nums)
ans = -inf
# for i in range(1,1<<n):
# s = 1
# for j in range(n):
# if i>>j&1:
# # print(j,nums[j])
# s *= nums[j]
# ans = max(ans,s)
# print(i,ans,s)
# def dfs(i,s,cnt):
# nonlocal ans
# if cnt:
# ans = max(ans,s)
# if i==n:
# return
# dfs(i+1,s,cnt)
# dfs(i+1,s*nums[i],cnt+1)
# dfs(0,1,0)
# return ans
mx = mn = nums[0]
for v in nums[1:]:
t = mx
mx = max(mx,v,v*mx,v*mn)
mn = min(mn,v,v*t,v*mn)
return mx
6464. 最大公约数遍历
6464. 最大公约数遍历
1. 题目描述
2. 思路分析
- 其实就是某些点之间有边,问最后是不是连通图(只有一个连通块)。
- n方建图当然不行,但是可以连虚拟节点,即把每个数字和它的所有质因数连起来。
- 那么开并查集连通对应下标和质因数即可。质因数作为虚拟节点,向右移动1e5位。因此并查集开大点。
- 连值也可以,需要特判count(1)>1 return false。
- 这样并查集就可以开小点,会快一些。
3. 代码实现
class PrimeTable:
def __init__(self, n: int) -> None:
self.n = n
self.primes = primes = [] # 所有n以内的质数
self.min_div = min_div = [0] * (n + 1) # md[i]代表i的最小(质)因子
min_div[1] = 1
# 欧拉筛O(n),顺便求出min_div
for i in range(2, n + 1):
if not min_div[i]:
primes.append(i)
min_div[i] = i
for p in primes:
if i * p > n: break
min_div[i * p] = p
if i % p == 0:
break
# # 埃氏筛O(nlgn),由于切片的原因,仅标记质数的场景下比线性筛表现更好。
# is_primes = [1] * (n + 1)
# is_primes[0] = is_primes[1] = 0 # 0和1不是质数
# for i in range(2, int((n + 1) ** 0.5) + 1):
# if is_primes[i]:
# is_primes[i * i::i] = [0] * ((n - 1 - i * i) // i + 1)
# self.primes = [i for i, v in enumerate(is_primes)]
def is_prime(self, x: int):
"""检测是否是质数,最坏是O(sqrt(x)"""
if x < 3: return x == 2
if x <= self.n: return self.min_div[x] == x
for i in range(2, int(x ** 0.5) + 1):
if x % i == 0: return False
return True
def prime_factorization(self, x: int):
"""分解质因数,复杂度
1. 若x>n则需要从2模拟到sqrt(x),如果中间x降到n以下则走2;最坏情况,不含低于n的因数,则需要开方复杂度
2. 否则x质因数的个数,那么最多就是O(lgx)"""
n, min_div = self.n, self.min_div
for p in range(2, int(x ** 0.5) + 1):
if x <= n: break
if x % p == 0:
cnt = 0
while x % p == 0: cnt += 1; x //= p
yield p, cnt
while 1 < x <= n:
p, cnt = min_div[x], 0
while x % p == 0: cnt += 1; x //= p
yield p, cnt
if x >= n and x > 1:
yield x, 1
def get_factors(self, x: int):
"""求x的所有因数,包括1和x"""
factors = [1]
for p, b in self.prime_factorization(x):
n = len(factors)
for j in range(1, b + 1):
for d in factors[:n]:
factors.append(d * (p ** j))
return factors
def mr_is_prime(self, x):
"""
Miller-Rabin 检测. 检测x是否是质数,置信度: 1 - (1/4)^k. 复杂度k*log^3
但是longlong以内可以用k==3或7的代价,换取100%置信度
https://zhuanlan.zhihu.com/p/349360074
"""
if x < 3 or x % 2 == 0:
return x == 2
if x % 3 == 0:
return x == 3
u, t = x - 1, 0
while not u & 1:
u >>= 1
t += 1
ud = (2, 325, 9375, 28178, 450775, 9780504, 1795265022) # long long 返回用这个7个数检测100%正确
# ud = (2, 7, 61) # int 返回用这3个数检测100%正确
# for _ in range(k):
# a = random.randint(2, x - 2)
for a in ud:
v = pow(a, u, x)
if v == 1 or v == x - 1 or v == 0:
continue
for j in range(1, t + 1):
v = v * v % x
if v == x - 1 and j != t:
v = 1
break
if v == 1:
return False
if v != 1:
return False
return True
class DSU:
"""基于数组的并查集"""
def __init__(self, n):
self.fathers = list(range(n))
self.size = [1] * n # 本家族size
self.edge_size = [0] * n # 本家族边数(带自环/重边)
self.n = n
self.set_count = n # 共几个家族
def find_fa(self, x):
fs = self.fathers
t = x
while fs[x] != x:
x = fs[x]
while t != x:
fs[t], t = x, fs[t]
return x
def union(self, x: int, y: int) -> bool:
x = self.find_fa(x)
y = self.find_fa(y)
if x == y:
self.edge_size[y] += 1
return False
# if self.size[x] > self.size[y]: # 注意如果要定向合并x->y,需要干掉这个;实际上上边改成find_fa后,按轶合并没必要了,所以可以常关
# x, y = y, x
self.fathers[x] = y
self.size[y] += self.size[x]
self.edge_size[y] += 1 + self.edge_size[x]
self.set_count -= 1
return True
pt = PrimeTable(10**5+5)
class Solution:
def canTraverseAllPairs(self, nums: List[int]) -> bool:
# if nums.count(1) >= 2:
# return False
n = len(nums)
dsu = DSU(2*10**5+5)
for i,v in enumerate(nums):
for p,k in pt.prime_factorization(v):
dsu.union(i,p+100000)
f = dsu.find_fa(0)
for i in range(1,n):
if dsu.find_fa(i) != f:
return False
return True





![[元带你学: eMMC协议详解 12] Speed Mode 选择](https://img-blog.csdnimg.cn/img_convert/262abfa94e2b5642120b21810384ce4b.png)