矩阵

直观理解

一个$m\times n$的大小矩阵，直观上看是$m\times n$的数字按矩阵排列。

从向量的角度看，看做是$n$个$m$维列向量从左到右的排列，也可以看做$m$个$n$维行向量从上到下的叠放。

特殊矩阵

1. 方阵：行数等于列数

2. 对称矩阵：原矩阵与其转置矩阵相等：$A=A^T$

   转置：原始矩阵行列互换后得到的新矩阵，称为原矩阵$A$的转置矩阵,记作：$A^T$

3. 行矩阵和列矩阵可以看做是向量

4. 零矩阵：元素全为0，记作：$O_{m\times n}$

5. 对角矩阵：非对角元素全部为0的方阵

6. 单位矩阵：对角元素全为1的对角矩阵

矩阵的基本运算

1. 矩阵加法：两个同等规模的矩阵之间，对应行列元素相加即可
2. 矩阵的数量乘法：将矩阵中每个元素都乘数乘的数

可见矩阵的运算系统中也包含线性运算

3. 矩阵与矩阵相乘，举例：$A$,$B$两个矩阵

   1. 首先如果想要得到$A\times B$的合法条件是，$A$的列数等于$B$的行数

   2. 左边矩阵决定了目标矩阵的行数

   3. 右边矩阵决定了目标矩阵的列数

   4. 具体运算：乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。

      

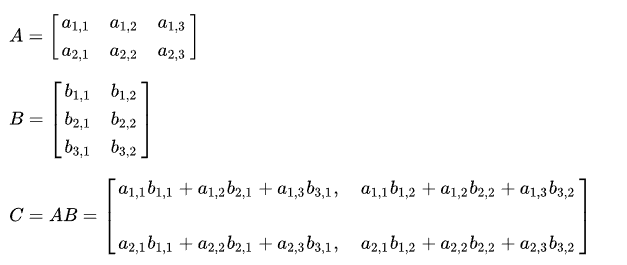
矩阵($A$)乘向量($x$)的本质：改变空间位置

矩阵乘向量的具体运算可以看成是矩阵相乘的特殊情况，不做过多介绍。

1. 从矩阵列的角度

   假设$A=[co{l}_{1}co{l}_2......co{l}_n]$,其中$col$表示矩阵列表示的向量

   $Ax=[co{l}_{1}co{l}_2......co{l}_n][x_1{x}_2...x_n{]}^T=x_{1}co{l}_1+x_{2}co{l}_2+...+x_{n}co{l}_n$

   可以看出：矩阵和向量相乘的过程就是对原矩阵的各列向量进行线性组合的过程，而线性组合的各系数就是向量的对应各成分。

2. 进一步引申：变换向量的基底

   $x=\left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]=x_1\left[\begin{array}{c}1\\ 0\\ ...\\ 0\end{array}\right]+x_2\left[\begin{array}{c}0\\ 1\\ ...\\ 0\end{array}\right]+...+x_n\left[\begin{array}{c}0\\ 0\\ ...\\ 1\end{array}\right]$​,向量$x$​表示为在基底为$(\left[\begin{array}{c}1\\ 0\\ ...\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\\ ...\\ 0\end{array}\right],...,\left[\begin{array}{c}0\\ 0\\ ...\\ 1\end{array}\right])$的坐标。

   我们来看一下在矩阵的作用下会发生怎样的变化。

   $Ax={\left[\begin{array}{ccc}{a}_{11}& \dots & a_{1n}\\ & \ddots & ⋮\\ a_{m1}& & a_{mn}\end{array}\right]}_{m\times n}\left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]=x_1\left[\begin{array}{c}{a}_{11}\\ a_{21}\\ ...\\ x_{m1}\end{array}\right]+x_2\left[\begin{array}{c}{a}_{12}\\ a_{22}\\ ...\\ x_{m2}\end{array}\right]+...+x_n\left[\begin{array}{c}{a}_{1n}\\ a_{2n}\\ ...\\ x_{mn}\end{array}\right]$

   可以看出矩阵对于向量的作用相当于对其基底做了映射转换，由旧基底转换为“新基底”。

   映射后向量维数取决于矩阵的行数。

   至于为啥”新基底“加引号，请往下看。

3. 特殊情况

   对于$m\times n$的矩阵$A$和$n$维列向量$x$，$x$的$n$个$n$维默认基向量构成的基底被转换成了$n$个$m$维的目标向量。

   • 当$n>m$时，这$n$个新向量线性相关，因此不能构成基底。
   • 当$n<m$时，这$n$个新向量不足以表示$R^m$向量空间的所有向量，也不能构成基底。
   • 当且仅当$n=m$并且这$n$个新向量线性无关时，才能被称为变换了基底

   以上所说的基底都是相对于$R^m$向量空间而言

矩阵：空间映射关系

由于矩阵的作用，原始向量的空间位置甚至其所在空间的维度和形态都发生了改变，这就是矩阵乘法的空间映射作用

以下假设矩阵$A$中的$n$个列向量线性无关

矮胖矩阵对空间的降维压缩

当$m<n$的时候，矩阵是一个外表"矮胖’的矩阵，向量$x$是$R^n$空间中的一个$n$维向量，$x$的$n$个基向量$e$分别被矩阵$A$映射成了$n$个$m$维向量，由于$m<n$，这一组目标向量所能张成的空间维数最大就是$m$。这样一来，在矩阵$A$的作用下，位于$R^n$空间中的任意向量$x$，经过映射作用，都转换到了一个维数更低的新空间中的新位置。由此我们看出，“矮胖"矩阵$A$压缩了原始空间$R^n$。

高瘦矩阵无法覆盖目标空间

简单来说就是高瘦矩阵通过对原向量空间的映射是不能够表示目标向量空间的所有向量的。

其实变换后的空间是不会增多的

$m\times n$矩阵中的$m>n$这种情况，我们称之为"高瘦"矩阵。
$x$的$n$个基向量$e$,分别被矩阵$A$映射成了$n$个$m$维向量，由于$m>n$，看上去$x$映射后的目标向量的维数提高了，变成了$m$维。那我们能不能说:经过矩阵$A$的映射，原始向量$x$构成的空间$R^n$变成了维数更高的空间$R^m$呢?答案是否定的，哲学点说，一个事物无中生有，那是不可能的，平白无故的一个向量携带的信息怎么能增加呢?

方阵映射

假设方阵$A_{n\times n}$

1. 当方阵$A$中$n$个列向量线性无关时，意味着原始向量的基被映射成新向量后，仍然可以构成$R^n$空间里的一组基底。
2. 当方阵$A$中$n$个列向量线性相关时，方阵则退化成了矮胖矩阵，参考前面所述即可。

矩阵的秩

我们把一个空间经过矩阵映射后得到的新空间称之为他的像空间。我们发现，一个原始空间，经过几个形状相同的矩阵进行映射，像空间的维数可能不同;经过几个不同形状的矩阵进行映射，又有可能得到维数相同的像空间。那么决定因素是什么?
决定因素就是空间映射矩阵的列向量，列向量张成空间的维数就是原始空间映射后的像空间维数。我们给矩阵列向量的张成空间维数取了一个名字，就叫作:矩阵的秩。从另一方面看，秩也可以说是该矩阵线性无关的列的个数。

间的维数可能不同;经过几个不同形状的矩阵进行映射，又有可能得到维数相同的像空间。那么决定因素是什么?
决定因素就是空间映射矩阵的列向量，列向量张成空间的维数就是原始空间映射后的像空间维数。我们给矩阵列向量的张成空间维数取了一个名字，就叫作:矩阵的秩。从另一方面看，秩也可以说是该矩阵线性无关的列的个数。