本篇文章来介绍一下整形在内存中的存储,内容丰富,干货慢慢。
目录
1.整形家族
2.整形在内存中的存储
3.大端小端存储
4.练习
1.整形家族
在开始之前,我们先来简单回顾一下整形家族:
char
unsigned char
signed char
short
unsigned short
signed short
int
unsigned int
signed short
long
unsigned long
signed long
long long
unsigned long long
signed long long
看到这里,我想肯定会有小伙伴问为什么 char 也属于整形家族,嘿嘿,那是因为 char 类型在内中存储的其实是字符对应的ASCII值,ASCII值也是整数,所以字符类型也归类到整形家族。
对于 unsigned (无符号)和 signed (有符号):生活中有些数值是有正值和负值,如温度,我们要用有符号类型来存储,我们在使用有符号类型时,signed 是可以省略不写的,例如 int 等同于 singed int ,但是要使用无符号类型时,unsigned 是不可以省略的,例如 unsigned int 。
这里值得注意的是,对于 char 类型来说:只写 char 到底是 unsigned char 还是 signed char C语言是没有明确规定的,只是有些编译器做了规定,如在VS编译器上,char 就等同于 signed char 。
2.整形在内存中的存储
变量的创建是要在内存中开辟空间的,空间的大小是根据不同的类型而决定的。
下来了解下面的概念∶
原码、反码、补码:
计算机中的整数有三种表示方法,即原码、反码和补码。
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示"负”,而数值位三种表示方法各不相同。
原码:
直接将二进制按照正负数的形式翻译成二进制就可以。符号位是二进制的第一位。
反码:
将原码的符号位不变,其他位依次按位取反就可以得到了。
补码:
反码加一就得到补码
正数的原、反、补码都相同。
对于整形来说:数据存放内存中其实存放的是补码。为什么呢?
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。这里不理解可以先往下看。
看下面一段代码:
在有符号类型中,二级制表示形式的第一位是符号位,后面位是数值位。
int main()
{
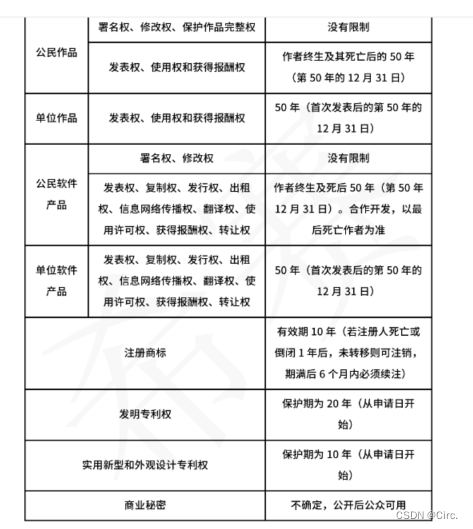
int num = 10;//创建一个整型变量,叫num,这时num向内存申请4个字节来存放数据
//整形4个字节 - 32个bit位(二进制位) 正整数原码,反码,补码相同
//00000000000000000000000000001010 - 原码
//00000000000000000000000000001010 - 反码
//00000000000000000000000000001010 - 补码
//0x 00 00 00 0a 16进制 a是10
int num2 = -10;
//10000000000000000000000000001010 - 原码
//11111111111111111111111111110101 - 反码
//11111111111111111111111111110110 - 补码
//0x FF FF FF F6 //16进制
return 0;
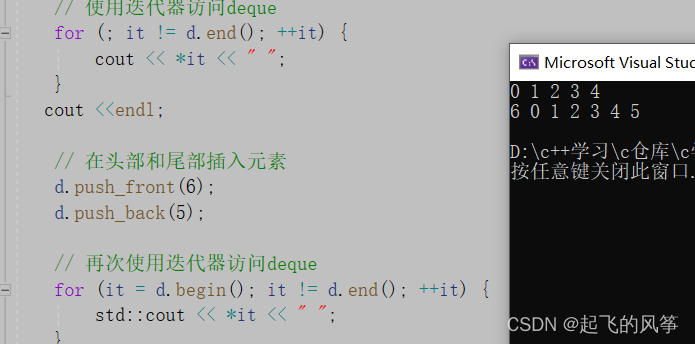
}我们可以通过调试,来查看内存中的数据,通过&num来得到num的地址,不知道如何调试的可以看我上篇关于如何调试的文章。 0x是表示后面的数是16进制数。
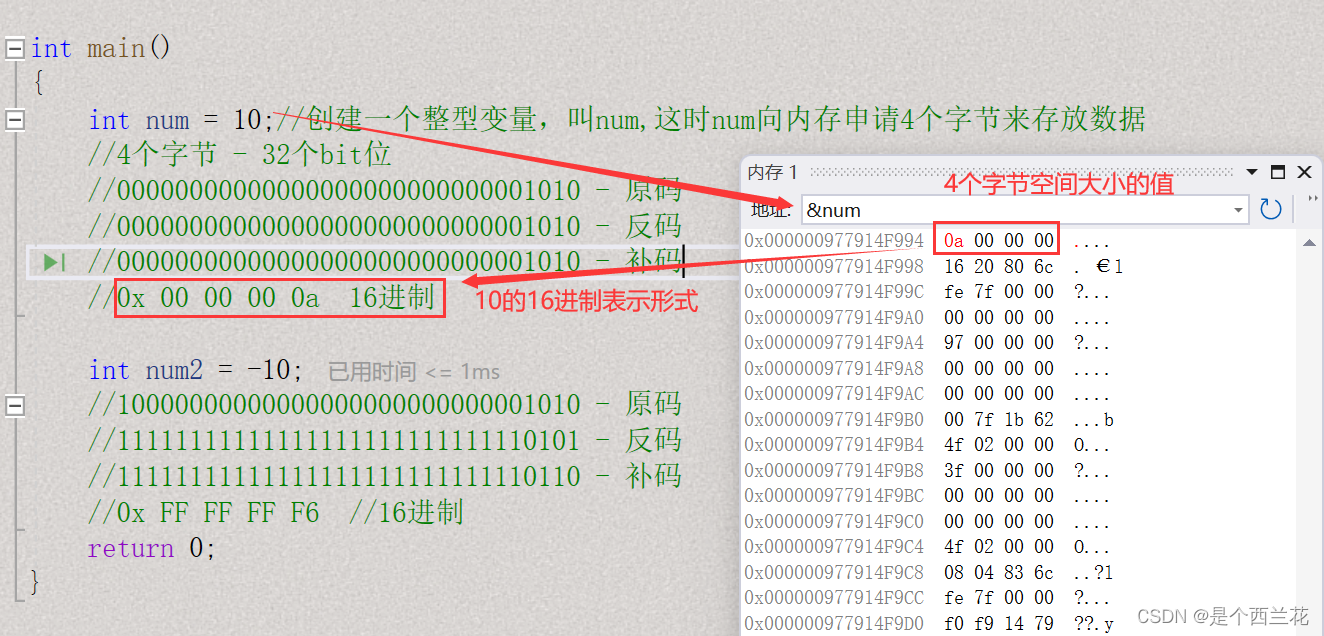
本质上内存中存放的是二进制,但VS为了方便显示,显示的是16进制,一个16进制位等于4个二进制位,因为16等于2的4次方。并且还可以发现数据在内存中是倒着存放的,关于为什么后面会讲。
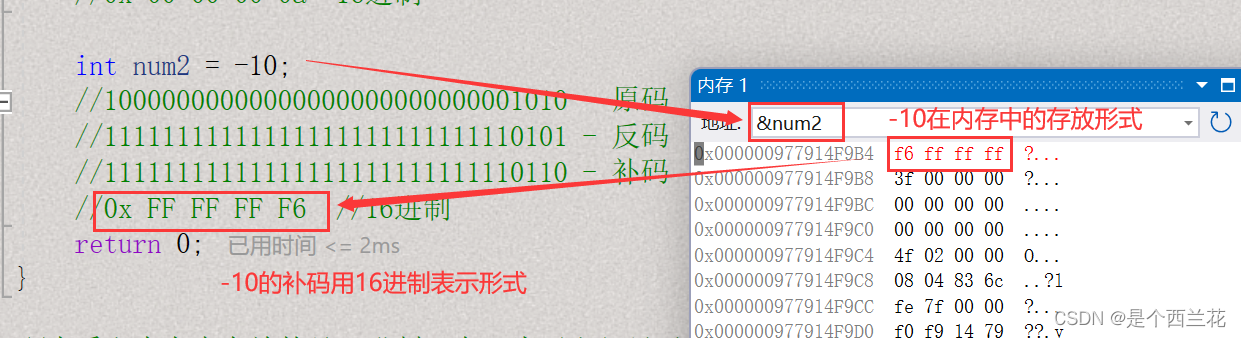
可以发现-10在内存中存放的是一个很大的数,也就是-10的补码。其实对于正整数来说,存放的也是它的补码,只不过是补码,反码,原码相同。
内存中的计算也是通过补码计算的:
上面说到计算机只有加法器,所以当我们计算减法时,是先将被减数换成负数再相加。
下面举一个例子计算1-1,换成加法就是1+(-1)
我们可以先用原码计算一下
00000000000000000000000000000001 1的原码
10000000000000000000000000000001 -1的原码相加,符号位也相加,得到:
10000000000000000000000000000010 -2
可以发现原码相加的得到是-2,是错误的。下面用补码计算
00000000000000000000000000000001 1的补码
10000000000000000000000000000001 -1的原码 我们把它转换为补码
1111111111111111111111111111111111110 -1的反码 (符号位不变,其他位按位取反)
1111111111111111111111111111111111111 -1的补码 (反码加一)将1的补码与-1的补码相加得到:
100000000000000000000000000000000 变成33位 要去掉最高位00000000000000000000000000000000 0 得到0
关于从补码得到原码,有两种方式:
1.通过 原码符号位不变,其他位取反得到反码,反码+1得到补码 这种方式反着推
2.补码 符号位不变,其他位取反,再+1就可得到原码,可以发现与原码得到补码得方式相同,想不到吧,这就是计算机发明者的智慧。
原码,反码,补码之间关系如下图所示:
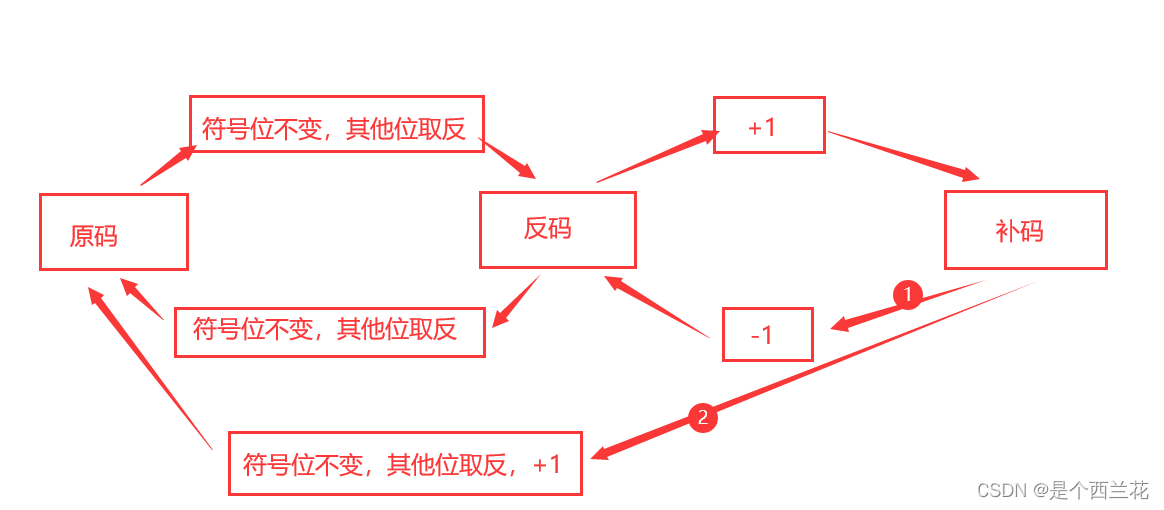
这里就可以理解为什么补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路了。
3.大端小端存储
什么是大端小端∶
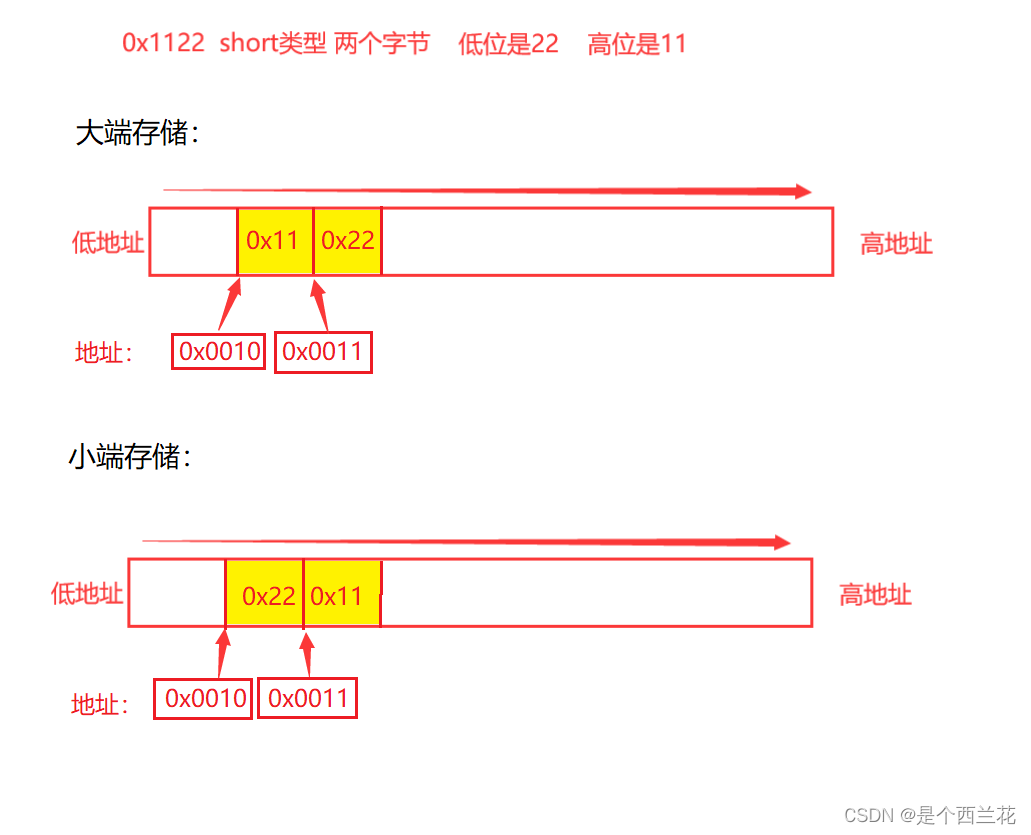
又称大端小端字节序,是以字节为单位,讨论存储顺序的,8个比特位(二进制位)或两个16进制是一个字节
大端(存储)模式,是指数据的低位保存在内存的高地址中,而数据的高位,保存在内存的低地址中;
小端(存储)模式,是指数据的低位保存在内存的低地址中,而数据的高位,,保存在内存的高地址中。为什么有大端和小端∶
为什么会有大小端模式之分呢?
这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为8bit。但是在C语言中除了8bit的char之外,还有16bit的short型,32bit的long型(要看具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如果将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。
例如一个16bit的short类型x变量,在内存中的地址为0x0010,x的值为0x1122,那么0x11为数据的高位,0x22为数据的地位。对于大端模式,就将0x11放在低地址中,即0x0010中,0x22放在高地址中,即0x0011中。小端模式,刚好相反。大端小端存储是由自己电脑的硬件来决定的。
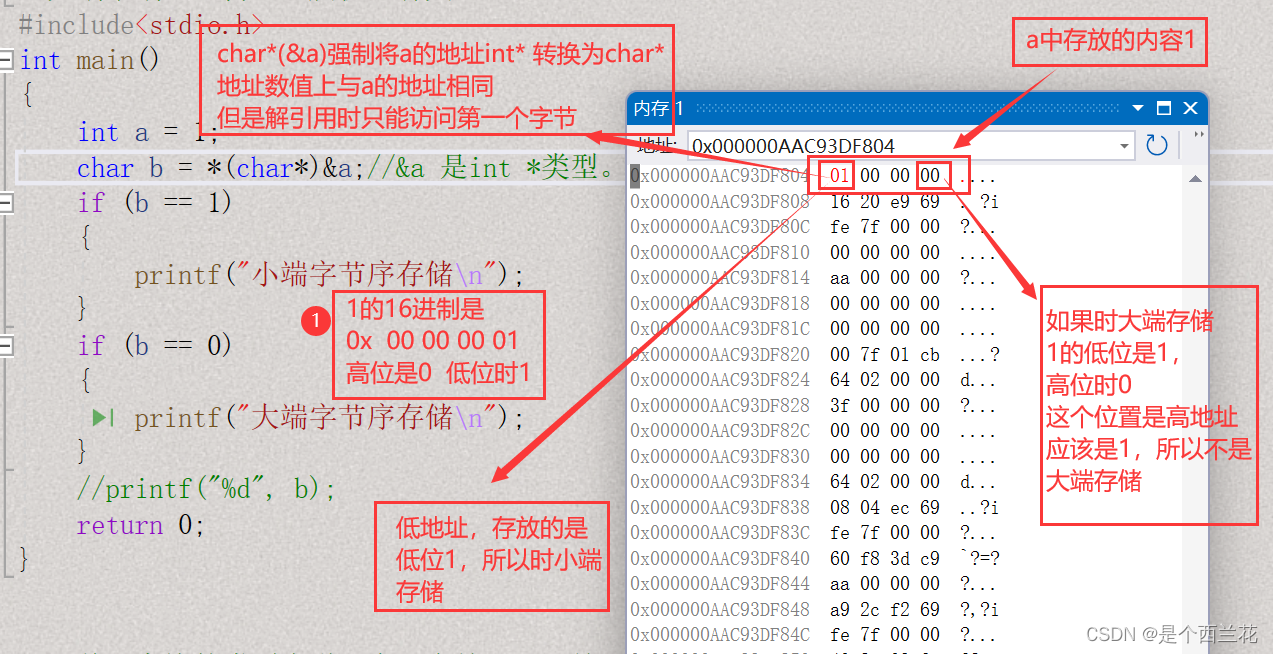
百度2015年系统工程师笔试题︰
请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)
#include<stdio.h>
int main()
{
int a = 1;
char b = *(char*)&a;//&a 是int *类型。
if (b == 1)
{
printf("小端字节序存储\n");
}
if (b == 0)
{
printf("大端字节序存储\n");
}
//printf("%d", b);
return 0;
}
4.练习
这里一起做做些练习,看看自己掌握的怎么样,顺便再讲一些干货。

1.
#include<stdio.h>
int main()
{
char a = -1;
//-1是整数发生截断
//11111111111111111111111111111111 -1补码
//11111111 a截断
signed char b = -1;
//与a相同
unsigned char c = -1;
//11111111111111111111111111111111 -1补码
//11111111 c截断
//%d 十进制打印有符号整形数据,发生整型提升
//整型提升时有符号高位补符号位,无符号补0
//a 11111111111111111111111111111111补码
// 11111111111111111111111111111110 反码
// 10000000000000000000000000000001 -1 原码打印
//b 和a相同
//c 111111111 无符号高位补0
// 00000000000000000000000011111111 255
printf("a=%d b=%d c=%d", a, b, c); -1 -1 255
return 0;
}2.
#include<stdio.h>
int main()
{
char a = -128;
//-128
//10000000000000000000000000001000000 -128原码
//11111111111111111111111111110111111 反码
//11111111111111111111111111111000000 补码
//10000000//截断
//打印整形提升
//11111111111111111111111111111000000
//补码按%u无符号打印 认为是无符号数,原反补相同,打印一个很大的数
printf("%u\n", a);
return 0;
}3. 与第2道结果相同
#include<stdio.h>
int main()
{
char a = 128;
//截断后是与-128截断后相同
//所以结果也与-128相同
printf("%u\n", a);
return 0;
}4.
#include<stdio.h>
int main()
{
int i = -20;
unsigned int j = 10;
printf("%d\n", i + j);
return 0;
}写到这里是不是有些不敢写-10了,没关系我们来推理一下
10000000000000000000000000010100 -20原码
111111111111111111111111111111101011 -20反码
111111111111111111111111111111101100 -20补码
00000000000000000000000000001010 10补码 与原码相同 与signed int 相同
111111111111111111111111111111110110 i + j 是补码
10000000000000000000000000001001 反码
10000000000000000000000000001010 -10 原码
5.
#include<stdio.h>
#include<Windows.h>
int main()
{
unsigned int i;//i恒大于0
for (i = 9; i >= 0; i--)//会死循环 打印很大的数
{
printf("%u\n", i);
}
return 0;
}那 i==0 后再 -1 是谁呢。 我们可以看一下 char 类型, -128到127
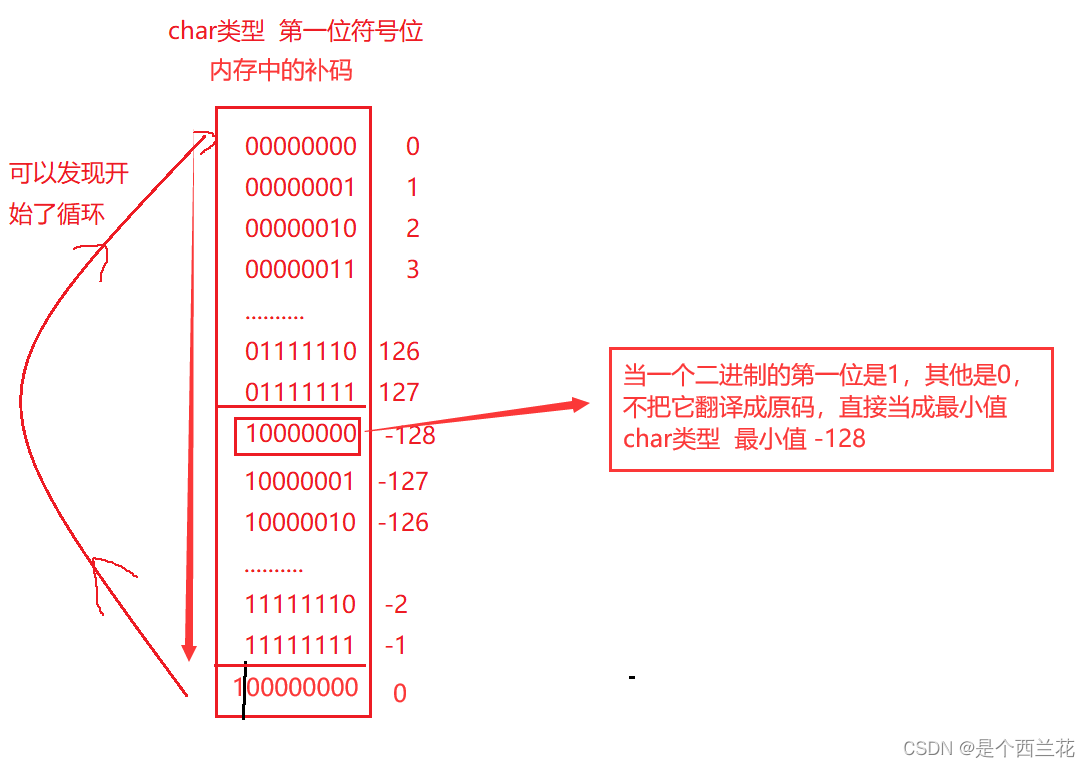
可以发现开始了循环,同理,当类型位为 unsigned char 时,最大值为255,在加一就是0。
知道了这一点,我们来做一下最后一道题
6.
#include<stdio.h>
int main()
{
char a[1000] = { 0 };
int i = 0;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}strlen是求的是 '\0' 之前的字符个数,而'\0'的ASCII码值是0,所以这里计算的是0之前的数组元素个数。
我们可以看 a 数组中的内容 -1,-2,-3 .... -127,-128,因为是char类型的数组,根据上面图片,所以后面是127,126,125 ...2,1,0,-1,... 之后再循环,我们统计 0 之前的元素个数,有128+127=255个,所以答案是255。
本篇结束,下篇讲浮点型数据在内存中的存储