以下内容大部分来源于《MATLAB智能算法30个案例分析》,仅为学习交流所用。
1理论基础
1.1遗传算法概述
遗传算法(genetic algorithm,GA)是一种进化算法,其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法则。遗传算法是把问题参数编码为染色体,再利用迭代的方式进行选择、交叉以及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。
在遗传算法中,染色体对应的是数据或数组,通常是由一维的串结构数据来表示,串上各个位置对应基因的取值。基因组成的串就是染色体,或者称为基因型个体(individuals)。一定数量的个体组成了群体(population)。群体中个体的数目称为群体大小(population size),也称为群体规模。而各个个体对环境的适应程度叫做适应度(fitness)。
遗传算法的基本步骤如下:
1.编码
GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。
2.初始群体的生成
随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。GA以这N个串结构数据作为初始点开始进化。
3.适应度评估
适应度表明个体或解的优劣性。不同的问题,适应性函数的定义方式也不同。4、选择
选择的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。遗传算法通过选择过程体现这一思想,进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。选择体现了达尔文的适者生存原则。
5.交叉
交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体,新个体组合了其父辈个体的特性。交叉体现了信息交换的思想。
6.变异
变异首先在群体中随机选择一个个体,对于选中的个体以一定的概率随机地改变串结构数据中某个串的值。同生物界一样,GA中变异发生的概率很低,通常取值很小。
1.2谢菲尔德遗传算法工具箱
1.工具箱简介
谢菲尔德(Sheffield)遗传算法工具箱是英国谢菲尔德大学开发的遗传算法工具箱。该工具箱是用MATLAB高级语言编写的,对问题使用M文件编写,可以看见算法的源代码,与此匹配的是先进的MATLAB数据分析、可视化工具、特殊目的应用领域工具箱和展现给使用者具有研究遗传算法可能性的一致环境。该工具箱为遗传算法研究者和初次实验遗传算法的用户提供了广泛多样的实用函数。
2.工具箱添加
用户可以通过网络下载gatbx工具箱(官方github下载地址:gatbx)。然后把工具箱添加到本机的MATLAB环境中,该工具箱的安装步骤如下:
(1)将工具箱文件夹复制到本地计算机中的工具箱目录下,路径为matlabroot\ toolbox。其中matlabroot为 MATLAB的安装根目录。
(2)将工具箱所在的文件夹添加到MATLAB的搜索路径中,有两种方式可以实现,即命令行方式和图形用户界面方式。
①命令行方式:用户可以调用addpath命令来添加,例如:
str = [matlabroot, '\toolbox\gatbx'];
addpath(str)②图形用户界面方式:在 MATLAB主窗口上选择主页→设置路径菜单项,单击“添加文件夹”按钮。找到工具箱所在的文件夹( gatbx),单击“OK”按钮,则工具箱所在的文件夹出现在“设置路径”的最上端。单击“保存”按钮保存搜索路径的设置,然后单击“关闭”按钮关闭对话框。

(3)批量修改后缀
该工具箱文件后缀为M,即*.M,matlab是区分大小写的,如果这一步没有操作,将会报错,在该文件路径下,新建txt,输入以下命令,并保存修改文件后缀为bat,点击运行:
ren *.M *.m如果文件夹中.M后缀的文件并未修改为.m的后缀,可以通过一个中间后缀名进行修改,先将其后缀名转为.txt,再转为.m,也就是先输入下面的命令,并保存修改文件后缀为bat,点击运行:
ren *.M *.txt所有.M后缀的文件都修改为了.txt后缀,然后再输入下面的命令并保存修改文件后缀为bat,点击运行:
ren *.txt *.m这样就把所有文件的后缀名都改成了.m文件。如果还是不行的话。。。。。就一个一个手动改吧。
2案例背景
2.1问题描述
1.简单一元函数优化
利用遗传算法寻找以下函数的最小值:
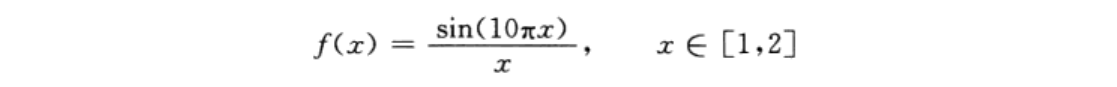
2.多元函数优化
利用遗传算法寻找以下函数的最大值:
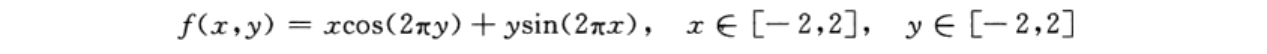
2.2解题思路及步骤
将自变量在给定范围内进行编码,得到种群编码,按照所选择的适应度函数并通过遗传算法中的选择,交叉和变异对个体进行筛选和进化,使适应度值大的个体被保留,小的个体被淘汰,新的群体继承了上一代的信息,又优于上一代,这样反复循环,直至满足条件,最后留下来的个体集中分布在最优解周围,筛选出其中最优的个体作为问题的解。
3 MATLAB程序实现
下面详细介绍各部分常用的函数,其他的函数用户可以直接参考工具箱中的GATBXA2.PDF文档,其中有详细的用法介绍。
3.1 工具箱结构
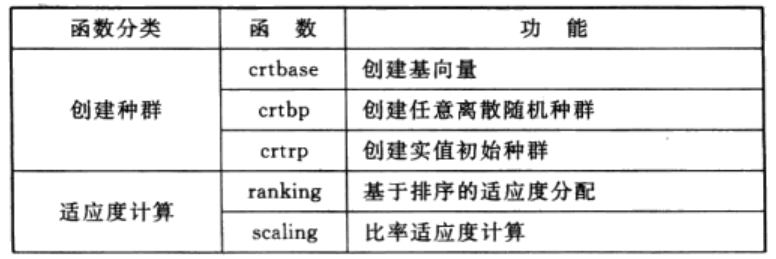
遗传算法工具箱中的主要函数如表1所列。
表1 遗传算法工具箱的主要函数列表

3.2遗传算法常用函数
1.创建种群函数——crtbp功能:创建任意离散随机种群。调用格式:
% 调用格式1
[Chrom,Lind,Basev]= crtbp(Nind,Lind)
% 调用格式2
[Chrom,Lind,Basev]= crtbp(Nind,Base)
% 调用格式3
[Chrom,Lind,Base]= crtbp(Nind,Lind,Base) 格式①创建一个大小为Nind×Lind 的随机二进制矩阵,其中,Nind 为种群个体数,Lind为个体长度。返回种群编码Chrom和染色体基因位的基本字符向量 BaseV。
格式②创建一个种群个体为Nind,个体的每位编码的进制数由Base 决定(Base 的列数即为个体长度)。
格式③创建一个大小为Nind×Lind 的随机矩阵,个体的各位的进制数由Base决定﹐这时输入参数Lind可省略(Base 的列数即为Lind),即为格式②。
【用法举例】使用函数crtbp创建任意离散随机种群的应用举例。
(1)创建一个种群大小为5,个体长度为10的二进制随机种群:
[Chrom,Lind,BaseV] = crtbp(5,10)
或者
[Chrom,Lind,BaseV] = crtbp(5,10,[2 2 2 2 2 2 2 2 2 2])
或者
[Chrom,Lind,BaseV] = crtbp(5,[2 2 2 2 2 2 2 2 2 2])
输出结果为:
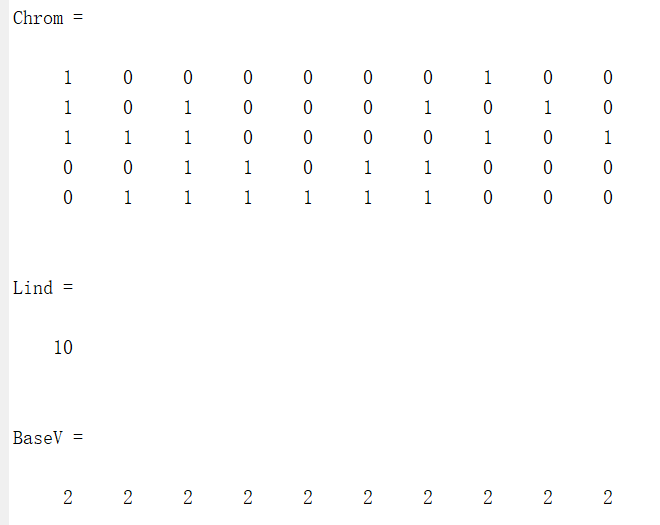
2.适应度计算函数一—ranking功能:基于排序的适应度分配。调用格式:
% 调用格式1
Fitnv = ranking(Objv)
% 调用格式2
Eitnv = ranking(Objv,RFun)
% 调用格式3
Fitnv = ranking(Objv,RFun,SUBPOP) 格式①是按照个体的目标值ObjV(列向量)由小到大的顺序对个体进行排序的,并返回个体适应度值FitnV的列向量。
格式②中RFun有三种情况: .
(1)若RFun是一个在[1,2]区间内的标量,则采用线性排序,这个标量指定选择的压差。
(2)若RFun是一个具有两个参数的向量,则RFun(2):指定排序方法,0为线性排序,1为非线性排序。RFun(1);对线性排序﹐标量指定的选择压差RFun(1)必须在[1,2]区间;对非线性排序,RFun(1)必须在[1, length(ObjV)一2]区间;如果为NAN,则 RFun(1)假设为2。
(3)若RFun是长度为length(ObjV)的向量,则它包含对每一行的适应度值计算。格式③中的参数ObjV和RFun与格式①和格式②一致,参数SUBPOP是一个任选参数,指明在-ObjV中子种群的数量。省略SUBPOP或SUBPOP为NAN,则 SUBPOP=1。在ObjV中的所有子种群大小必须相同。如果ranking被调用于多子种群,则ranking 独立地对每个子种群执行。
【用法举例】考虑具有10个个体的种群,其当前目标值如下:
ObjV = [1;2;3;4;5;10;9;8;7;6](1)使用线性排序和压差为⒉估算适应度:
Fitnv= ranking(ObjV)
% 或者
Fitnv= ranking(ObjV,[2,0])
% 或者
Fitnv= ranking(ObjV,[2,0],1)运行结果如下:

(2〉使用RFun中的值估算适应度:
RFun = [3;5;7;10;14;18;25;30;40;50];
Fitnv = ranking(Objv, RFun)运行结果:
(3〉使用非线性排序,选择压差为2,在ObjV中有两个子种群估算适应度:
FitnV =ranking(ObjV,[2,1],2)运行结果:
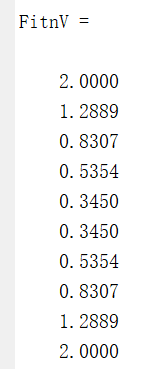
3.选择函数——select 功能:从种群中选个体(高级函数)。 调用格式:
selCh = select(SEL_F,Chrom,Fitnv)
selCh = select(SEL_r,Chrom,Eitnv,GGAP)
selCh = select(SRL_F,Chrom,Fitnv,GGAP,SUBPOP)SEL_F是一个字符串,包含一个低级选择函数名,如 rws 或 sus;
FitnV是列向量,包舍种群 Chrom中个体的适应度值。这个适应度值表明了每个个体被 选择的预期概率。
GGAP是可选参数,指出了代沟部分种群被复制。如果GGAP省略或为NAN,则GAP 假设为1.0。
SUBPOP是一个可选参数,决定 Chrom 中子种群的数量。如果 SUBPOP 省略或为 NAN,则 sUBPOP=1。Chrom 中所有子种群必须有相同的大小。
【用法举例】考虑以下具有8个个体的种群Chrom,适应度值为FitnV:
Chrom = [1 11 21;2 12 22;3 13 23;4 14 24;5 15 25;6 16 26;7 17 27;8 18 28]
FitnV = [1.50;1.35;1.21;1.07;0.92;0.78;0.64;0.5]使用随机遍历抽样 sus 选择8个个体
selch = select('sus',Chrom,FitnV)运行结果为:
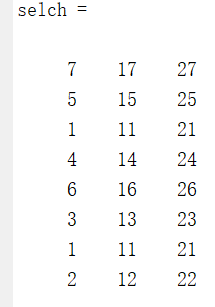
4.交叉算子函数——recombin功能:重组个体(高级函数)。调用格式:
NewChrom = recombin(REC_r,Chrom)
NewChrom = recombin(REC_F,Chrom,Recopt)
NewChrom = recombin(REC_F,Chrom,RecOpt,SUBPOP) recombin完成种群Chrom中个体的重组,在新种群NewChrom中返回重组后的个体。Chrom和NewChrom中的一行对应一个个体。
REC_F是一个包含低级重组函数名的字符串,例如recdis或xovsp.
RecOpt是一个指明交叉概率的任选参数,如省略或为NAN,将设为缺省值。
SUBPOP是一个决定Chrom中子群个数的可选参数,如果省略或为NAN,则 SUBPOP为1。Chrom中的所有子种群必须有相同的大小。
【用法举例】使用函数recombin对5个个体的种群进行重组。
Chrom = crtbp(5,10)
NewChrom = recombin('xovsp',Chrom)
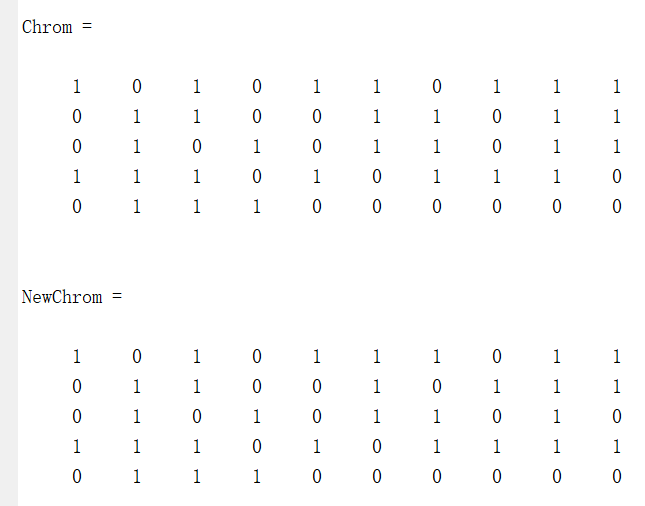
5.变异算子函数——mut功能:离散变异算子。
调用格式:
NewChrom = mut(O1dChrom,Pm,Basev)OldChrom为当前种群,Pm为变异概率(省略时为0.7/Lind),BaseV指明染色体个体元素的变异的基本字符(省略时种群为二进制编码)。
【用法举例】使用函数mut将当前种群变异为新种群。
(1)种群为二进制编码:
oldChrom = crtbp(5,10)
NewChrom = mut(oldChrom)
(2)种群为非二进制编码,创建一个长度为8、有6个个体的随机种群;
BaseV = [8 8 8 4 4 4 4 4];
[Chrom, Lind,BaseV] = crtbp(6,BaseV);
Chrom
NewChrom = mut(Chrom,0.7,BaseV)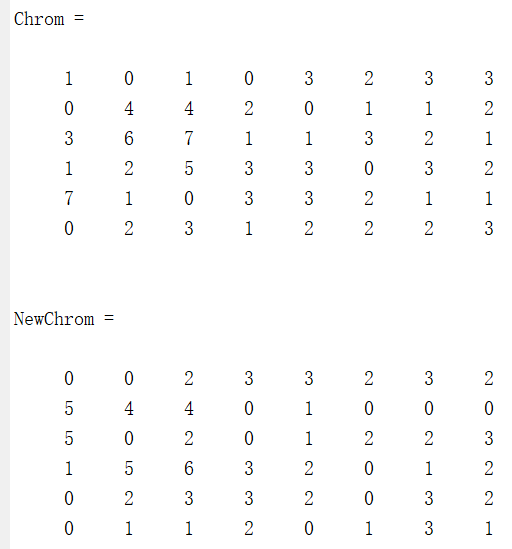
6.重插入函数———reins功能:重插入子代到种群。调用格式:
Chrom = reins(Chrom,SelCh)
Chrom = reins(Chrom,Se1Ch,SUBPOP)
Chrom = reins(Chrom,SelCh,SUBPOP, InsOpt,0bjvCh)
[Chrom,0bjVCh]= reins(Chrom,SelCh,SUBPOP,Ins0pt,0bjvCh,0bjvSel) reins完成插人子代到当前种群,用子代代替父代并返回结果种群。Chrom为父代种群,SelCh为子代,每一行对应一个个体。
SUBPOP是一个可选参数,指明Chrom和 SelCh中子种群的个数。如果省略或者为NAN,则假设为1。在Chrom和SelCh中每个子种群必须具有相同大小。
InsOpt是一个最多有两个参数的任选向量。
InsOpt(1)是一个标量,指明用子代代替父代的方法。0为均匀选择,子代代替父代使用均匀随机选择。1为基于适应度的选择,子代代替父代中适应度最小的个体。如果省略InsOpt(1)或InsOpt(1)为NAN,则假设为0。
InsOpt(2)是一个在[o,1]区间的标量,表示每个子种群中重插入的子代个体在整个子种群中个体的比率。如果InsOpt(2)省略或为NAN,则假设InsOpt(2)=1.0。
ObjVCh是一个可选列向量,包括Chrom中个体的目标值。对基于适应度的重插入,ObjVCh是必需的。
ObjVSel是一个可选参数,包含SelCh中个体的目标值。如果子代的数量大于重插入种群中的子代数量﹐则ObjVSel是必需的。这种情况子代将按它们的适应度大小选择插人。
【用法举例】在5个个体的父代种群中插入子代种群。
Chrom = crtbp(5,10) % 父代
selch = crtbp(2,10) % 子代
Chrom = reins(Chrom,selch) % 重插入
7.实用函数——bs2rv
功能:二进制到十进制的转换。调用格式:
Phen = bs2rv(Chrom,FieldD) bs2rv根据译码矩阵FieldD将二进制串矩阵Chrom 转换为实值向量,返回十进制的矩阵。
矩阵FieldD有如下结构:
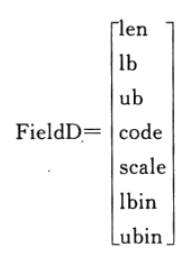
这个矩阵的组成如下:
len是包含在Chrom中的每个子串的长度,注意sum(len)=size(Chrom,2)。lb和ub分别是每个变量的下界和上界。
code指明子串是怎样编码的,1为标准的二进制编码,0为格雷编码。scale指明每个子串所使用的刻度,0表示算术刻度,1表示对数刻度。
lbin和 ubin指明表示范围中是否包含边界。0表示不包含边界,1表示包含边界。
【用法举例】先使用crtbp创建二进制种群Chrom,表示在[一1,10]区间的一组简单变量,然后使用bs2rv将二进制串转换为实值表现型。
Chrom = crtbp(4,8) % 创建二进制串
FieldD = [size(Chrom,2);-1;10;1;0;1;1] % 包含边界
Phen = bs2rv(Chrom,FieldD) % 转换二进制到10进制
8.实用函数—-rep功能:矩阵复制。
调用格式: Matout = rep(MatIn,REPN)
函数rep完成矩阵MatIn的复制,REPN指明复制次数,返回复制后的矩阵 MatOut。REPN包含每个方向复制的次数,REPN(1)表示纵向复制次数,REPN(2)表示水平方向复制次数。
【用法举例】使用函数rep 复制矩阵MatIn。
MatIn = [1 2 3 4;5 6 7 8]
MatOut = rep(MatIn,[1,2]) 
3.3遗传算法工具箱应用举例
本节通过一些具体的例子来介绍遗传算法工具箱函数的使用。
1.简单一元函数优化
利用遗传算法计算以下函数的最小值:
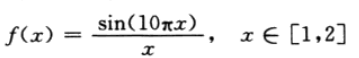
选择二进制编码,遗传算法参数设置如表2所列。
表2 遗传算法参数

遗传算法优化程序代码:
clc
clear all
close all
%% 画出函数图
figure(1);
hold on;
lb=1;ub=2; %函数自变量范围【1,2】
ezplot('sin(10*pi*X)/X',[lb,ub]); %画出函数曲线
xlabel('自变量/X')
ylabel('函数值/Y')
%% 定义遗传算法参数
NIND=40; %个体数目
MAXGEN=20; %最大遗传代数
PRECI=20; %变量的二进制位数
GGAP=0.95; %代沟
px=0.7; %交叉概率
pm=0.01; %变异概率
trace=zeros(2,MAXGEN); %寻优结果的初始值
FieldD=[PRECI;lb;ub;1;0;1;1]; %区域描述器
Chrom=crtbp(NIND,PRECI); %初始种群
%% 优化
gen=0; %代计数器
X=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换
ObjV=sin(10*pi*X)./X; %计算目标函数值
while gen<MAXGEN
FitnV=ranking(ObjV); %分配适应度值
SelCh=select('sus',Chrom,FitnV,GGAP); %选择
SelCh=recombin('xovsp',SelCh,px); %重组
SelCh=mut(SelCh,pm); %变异
X=bs2rv(SelCh,FieldD); %子代个体的十进制转换
ObjVSel=sin(10*pi*X)./X; %计算子代的目标函数值
[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代,得到新种群
X=bs2rv(Chrom,FieldD);
gen=gen+1; %代计数器增加
%获取每代的最优解及其序号,Y为最优解,I为个体的序号
[Y,I]=min(ObjV);
trace(1,gen)=X(I); %记下每代的最优值
trace(2,gen)=Y; %记下每代的最优值
end
plot(trace(1,:),trace(2,:),'bo'); %画出每代的最优点
grid on;
plot(X,ObjV,'b*'); %画出最后一代的种群
hold off
%% 画进化图
figure(2);
plot(1:MAXGEN,trace(2,:));
grid on
xlabel('遗传代数')
ylabel('解的变化')
title('进化过程')
bestY=trace(2,end);
bestX=trace(1,end);
fprintf(['最优解:\nX=',num2str(bestX),'\nY=',num2str(bestY),'\n'])
运行结果:

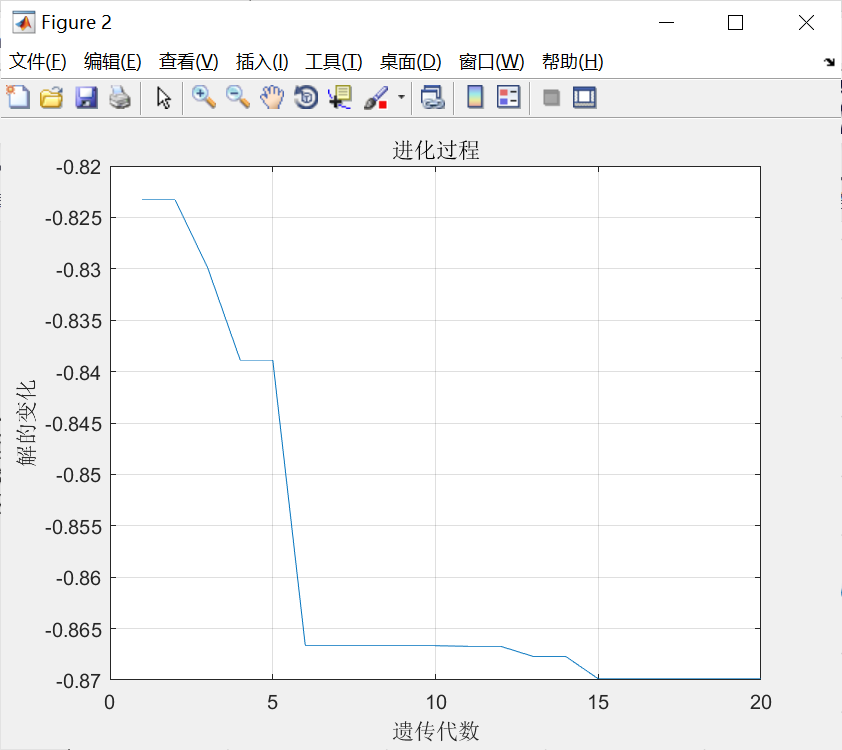
2.多元函数优化
利用遗传算法计算以下函数的最大值:
![]()
选择二进制编码,遗传算法参数设置如表3所列。
表3 遗传算法参数

遗传算法优化程序代码:
clc
clear all
close all
%% 画出函数图
figure(1);
lbx=-2;ubx=2; %函数自变量x范围【-2,2】
lby=-2;uby=2; %函数自变量y范围【-2,2】
ezmesh('y*sin(2*pi*x)+x*cos(2*pi*y)',[lbx,ubx,lby,uby],50); %画出函数曲线
hold on;
%% 定义遗传算法参数
NIND=40; %个体数目
MAXGEN=50; %最大遗传代数
PRECI=20; %变量的二进制位数
GGAP=0.95; %代沟
px=0.7; %交叉概率
pm=0.01; %变异概率
trace=zeros(3,MAXGEN); %寻优结果的初始值
FieldD=[PRECI PRECI;lbx lby;ubx uby;1 1;0 0;1 1;1 1]; %区域描述器
Chrom=crtbp(NIND,PRECI*2); %初始种群
%% 优化
gen=0; %代计数器
XY=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjV=Y.*sin(2*pi*X)+X.*cos(2*pi*Y); %计算目标函数值
while gen<MAXGEN
FitnV=ranking(-ObjV); %分配适应度值
SelCh=select('sus',Chrom,FitnV,GGAP); %选择
SelCh=recombin('xovsp',SelCh,px); %重组
SelCh=mut(SelCh,pm); %变异
XY=bs2rv(SelCh,FieldD); %子代个体的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjVSel=Y.*sin(2*pi*X)+X.*cos(2*pi*Y); %计算子代的目标函数值
[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代,得到新种群
XY=bs2rv(Chrom,FieldD);
gen=gen+1; %代计数器增加
%获取每代的最优解及其序号,Y为最优解,I为个体的序号
[Y,I]=max(ObjV);
trace(1:2,gen)=XY(I,:); %记下每代的最优值
trace(3,gen)=Y; %记下每代的最优值
end
plot3(trace(1,:),trace(2,:),trace(3,:),'bo'); %画出每代的最优点
grid on;
plot3(XY(:,1),XY(:,2),ObjV,'bo'); %画出最后一代的种群
hold off
%% 画进化图
figure(2);
plot(1:MAXGEN,trace(3,:));
grid on
xlabel('遗传代数')
ylabel('解的变化')
title('进化过程')
bestZ=trace(3,end);
bestX=trace(1,end);
bestY=trace(2,end);
fprintf(['最优解:\nX=',num2str(bestX),'\nY=',num2str(bestY),'\nZ=',num2str(bestZ),'\n'])
运行结果:
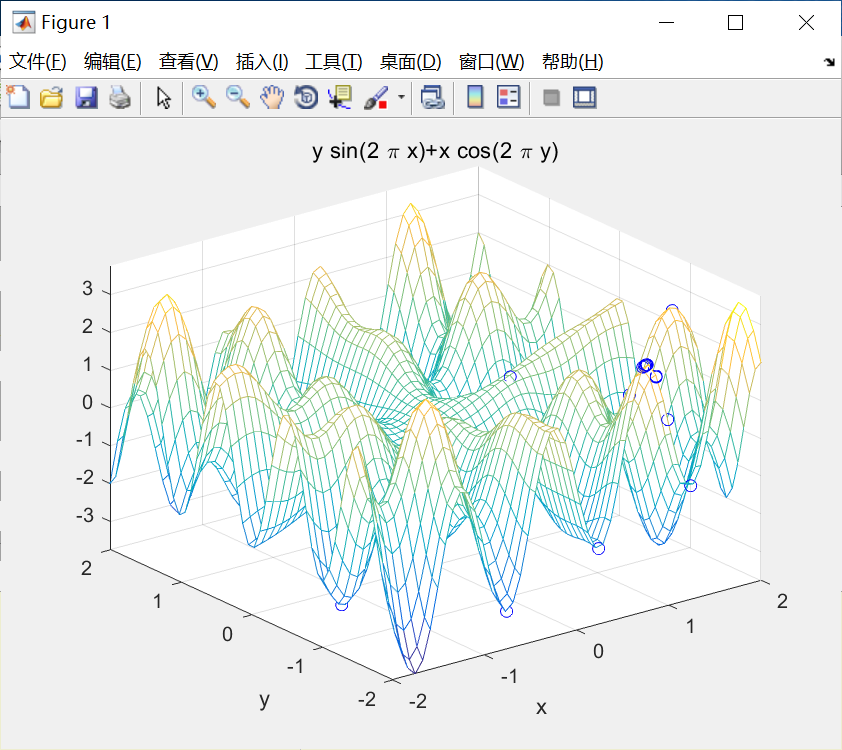
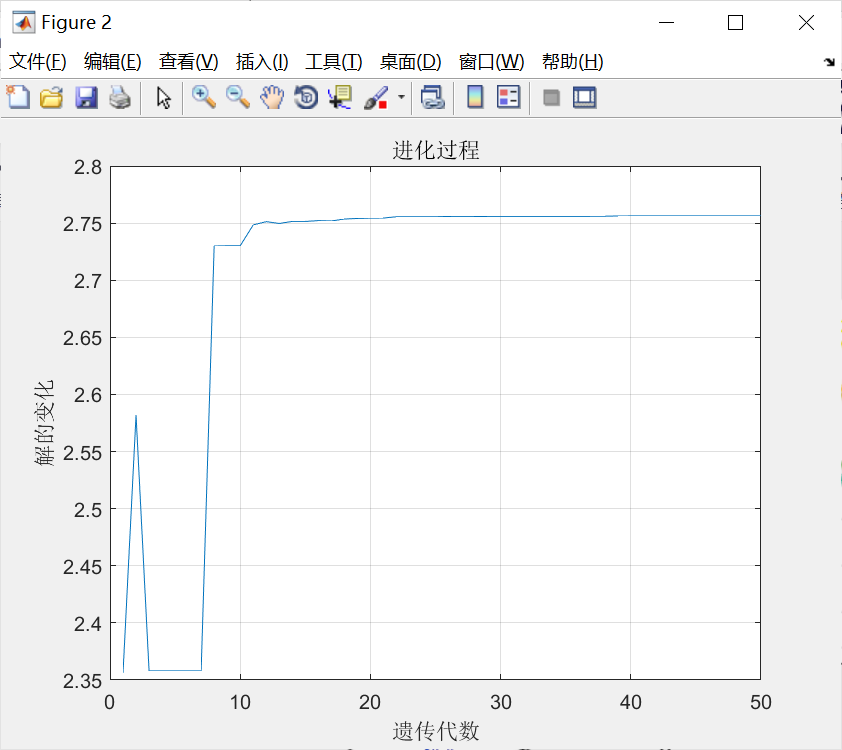
4.总结
遗传算法工具箱提供了一种求解非线性、多模型、多目标等复杂系统优化问题的通用框架,它不依赖问题的具体领域,对问题的种类具有很强的鲁棒性,所以它广泛应用于各个科学领域。遗传算法在函数优化、组合优化、生产调度、自动控制﹑机器人学﹑图像处理、人工生命、遗传编码和机器学习等方面得到了广泛运用。