二叉搜索树的实现(C语言)

news2024/11/29 0:56:46

目录

前言：

一：准备工作

(1)需要的头文件

(2)树节点结构体描述

(3)初始化

二：指针

三：插入新节点(建树)

(1)生成一个新节点

(2)找插入位置

四：查找和遍历

(1)查找

(2)遍历

五：删除节点

六：全部代码

(1)BinarySearchTree.h(声明)

(2)BinarySearchTree.c(函数具体实现)

(3)test.c(测试)

前言：

二叉搜索树（Binary Search Tree，BST）是一种非常常见的数据结构，它是一个二叉树，其中每个节点都包含一个键值。

对于任何一个结点，它的左子树中的所有键值都小于它的键值，右子树中的所有键值都大于它的键值。基于这样的特性，我们只需要依据根节点的数据域来判断目标节点是在根节点的左子树中还是右子树中，从而提高查找效率。

这种特殊的性质使得对于一个含有N个结点的二叉搜索树，对它进行查找和插入操作的时间复杂度不超过O(logN)，是一种非常高效的数据结构。

注意：本文采用递归来实现，但我不会详细讲递归展开的思路，强烈建议大家先掌握二叉树遍历的递归实现再来看本文(理解不了也可以画一下递归展开图)。

二叉树基本接口递归实现：https://blog.csdn.net/2301_76269963/article/details/130231257?spm=1001.2014.3001.5502

一：准备工作

(1)需要的头文件

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

(2)树节点结构体描述

//重定义数据类型，方便以后更改
typedef int BSTData;

typedef struct BSTNode
{
	//数据域
	BSTData data;
	//指针域，左孩子和右孩子
	struct BSTNode* LeftChild;
	struct BSTNode* RightChild;
}BSTNode;

(3)初始化

    //定义一个结构体指针，初始化为空
	BSTNode* root = NULL;

二：指针

插入新节点和删除节点有可能需要修改节点的指针域，因此需要传入二级指针来进行修改(C需要)，为了方便大家理解后续树的结构调整，我单独讲一下。

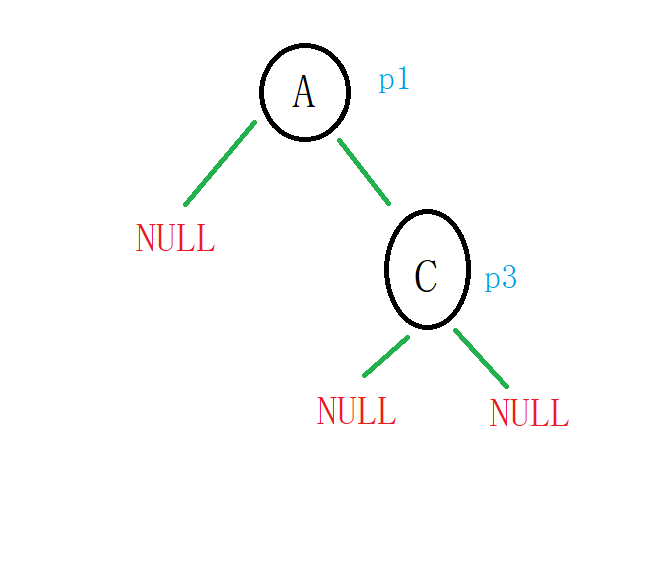
我们看下面这颗树：

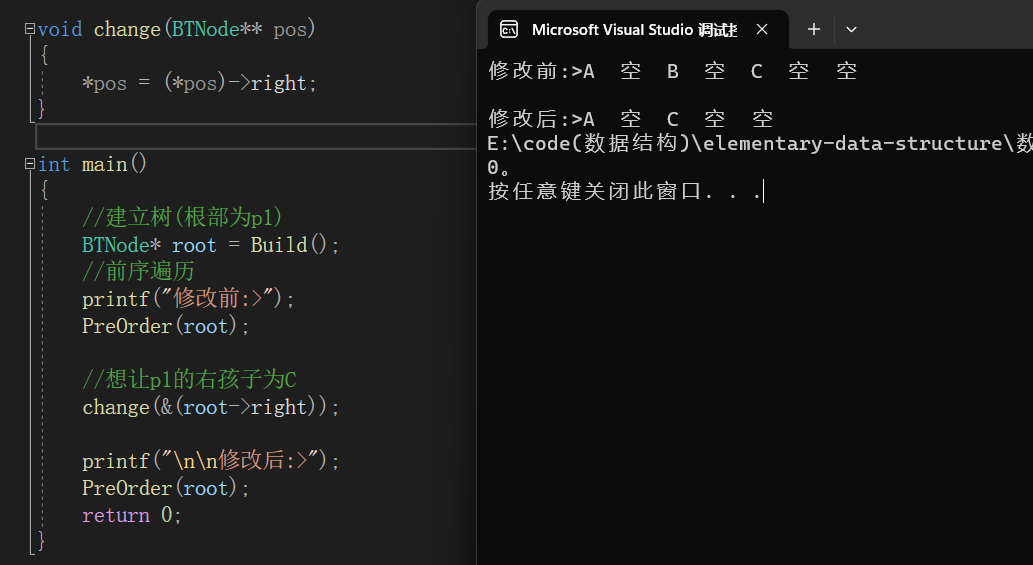
如果我们要让p1的右孩子为C(即修改p1的指针域)，下面这段代码可以吗？

答案当然是不行

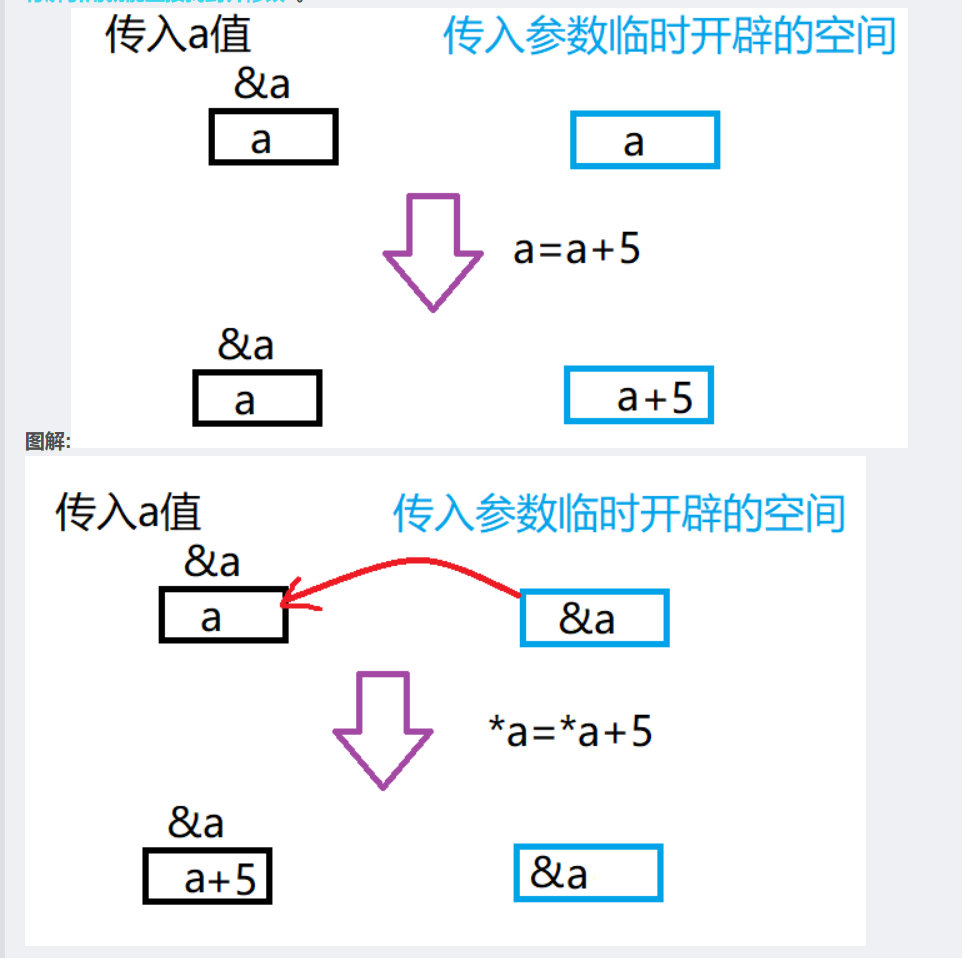
原因：形参不过是实参的一份临时拷贝，两者在不同空间，你给了我结构体指针，我可以通过指针找到结构体空间并修改成员，但要更改这个指针本身是做不到的。

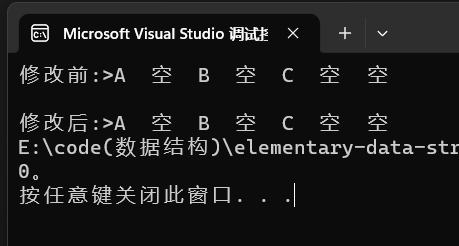
就像这个代码一样：

我们可以传二级指针来进行修改，虽然依然是一份临时拷贝，但是可以通过这个二级指针找到一级指针空间来进行修改。

三：插入新节点(建树)

(1)生成一个新节点

//生成一个新结点，很简单
BSTNode* BuyNewNode(BSTData x)
{
	BSTNode* NewNode = (BSTNode*)malloc(sizeof(BSTNode));
	if (NewNode == NULL)
	{
		printf("malloc error\n");
		exit(-1);
	}
	NewNode->LeftChild = NewNode->RightChild = NULL;
	NewNode->data = x;
	return NewNode;
}

(2)找插入位置

插入新节点后要保证二叉树任何一个结点，它的左子树中的所有键值都小于它的键值，右子树中的所有键值都大于它的键值。

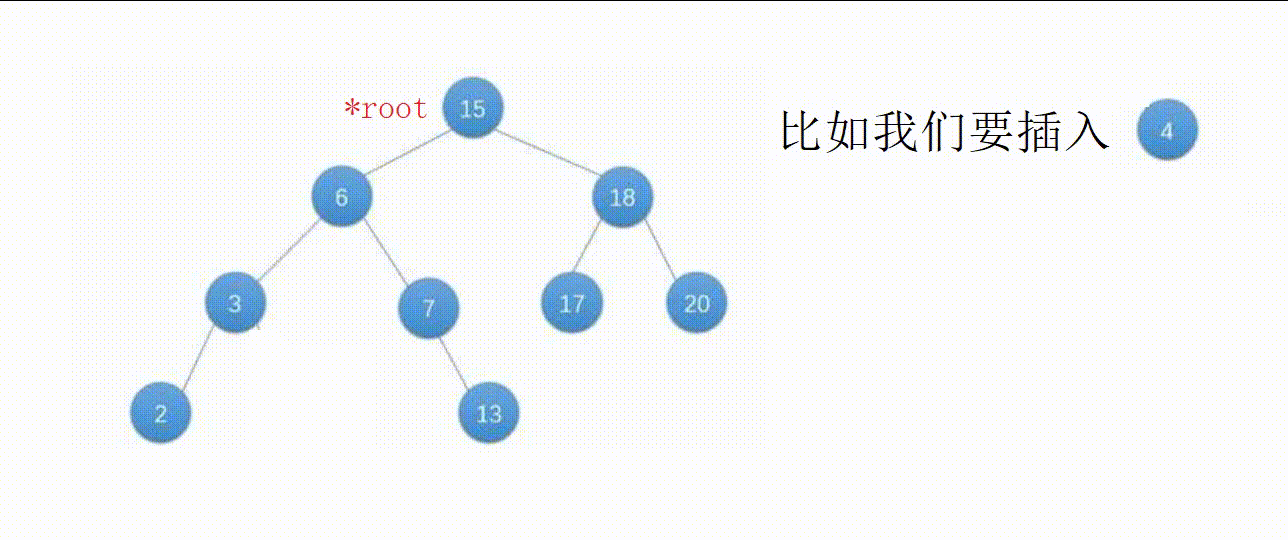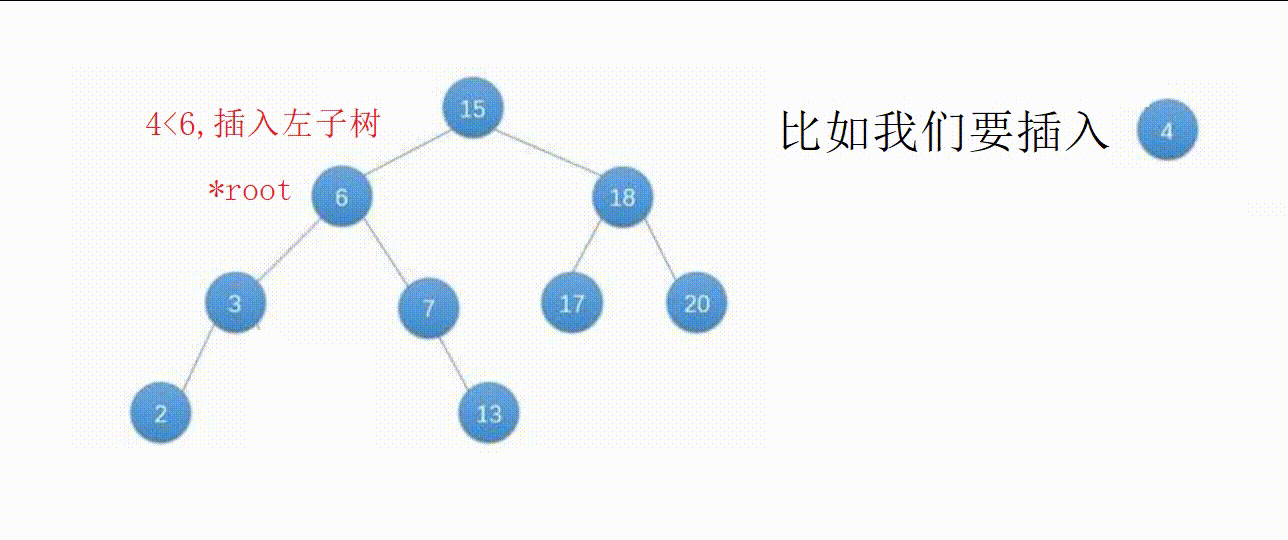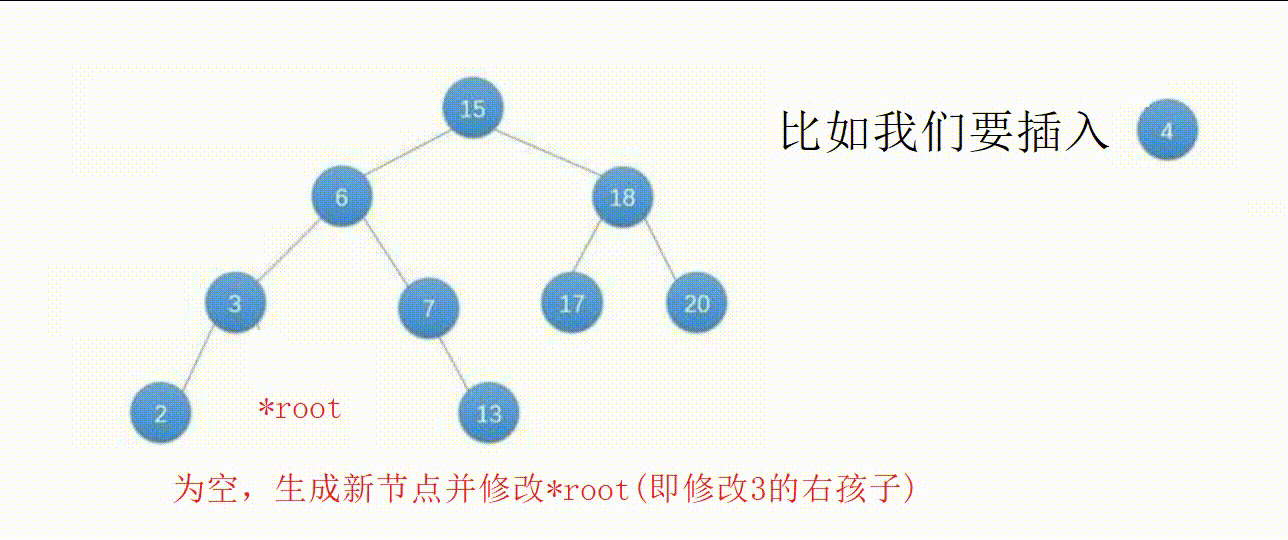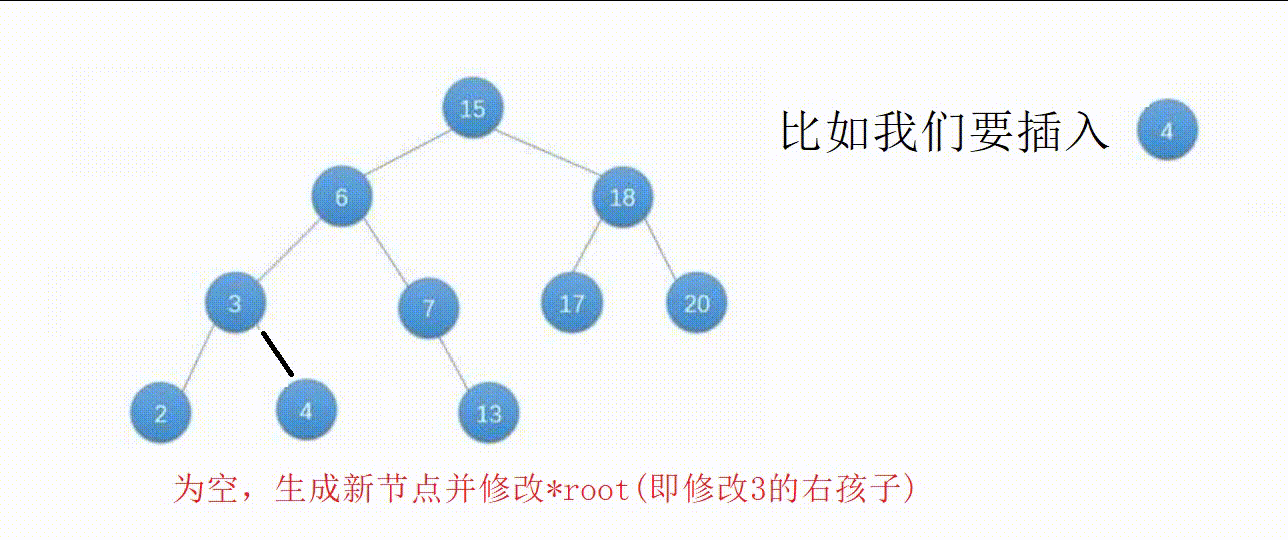
【1】设待插入数据为x。

【2】如果根部节点的值大于x，我们要把新节点插入到左子树中，小于x插入到右子树中，等于x不可以插入(如果搜索二叉树允许相同数据，那么相同的数据会放在同一个节点上，会导致树的结构变得不平衡，甚至可能会退化成链表。这样会极大地影响搜索二叉树的搜索效率，而且也违反了搜索二叉树的定义)。

【3】按这个思路向下递归，一直到空节点，这个位置就是适合插入的位置。

图解：

 

代码：

//搜索二叉树插入,成功返回0，失败返回-1
//可能改变指针域，传二级
int BSTInsert(BSTNode** root, BSTData x)
{
	//如果为空，生成一个新结点并链接
	if (*root == NULL)
	{
		BSTNode* NewNode = BuyNewNode(x);
		*root = NewNode;
		return 0;
	}
	//不为空，看是插入右子树中还是左子树中
	//小于插入左子树
	if (x < (*root)->data)
	{
		return BSTInsert(&(*root)->LeftChild, x);
	}
	//大于插入右子树
	else if (x > (*root)->data)
	{
		return BSTInsert(&(*root)->RightChild, x);
	}
	//相等不能插入，返回-1
	else
	{
		return -1;
	}
}

四：查找和遍历

(1)查找

查找的思路和找插入位置基本是一样的。

【1】设待查找数据为x。

【2】如果根部节点的值大于x，目标节点只可能在左子树中，小于x目标节点只可能在右子树中，等于就找到了目标节点，返回节点地址。

【3】按这个思路向下递归，如果到空节点，说明树中没有这个节点，返回空。

图解：

 

代码：

//搜索二叉树查找,查找到返回结点地址，否则返回空指针
BSTNode* BSTFind(BSTNode* root, BSTData x)
{
	//如果这个结点是目标结点或者 
	//已经走到空(未找到返回空)
	if ((root->data == x) || (root == NULL))
	{
		return root;
	}

	//不是就查找子树，比x大在右树中查找，小在左树中查找
	if (x > root->data)
	{
		return BSTFind(root->RightChild, x);
	}
	else
	{
		return BSTFind(root->LeftChild, x);
	}
}

(2)遍历

遍历就不细讲了，文章开头的链接有，这里只是想单独讲一点。

基于搜索二叉树的性质，我们采用中序遍历的方式(先遍历左子树再访问根部节点最后遍历右子树)来遍历二叉搜索树，会得到一个有序的序列，利用中序遍历可以方便我们观察搜索二叉树的创建是否成功以及还原树的逻辑结构。

 

代码：

//搜索二叉树遍历(中序)
void InOrder(BSTNode* root)
{
	if (root == NULL)
	{
		printf("空 ");
		return;
	}
	InOrder(root->LeftChild);
	printf("%d ", root->data);
	InOrder(root->RightChild);
}

五：删除节点

找到待删除节点并不困难，难点在于删除后维持搜索二叉树的结构，我们可以把删除节点分成四种情况。

①节点不存在，直接返回-1即可

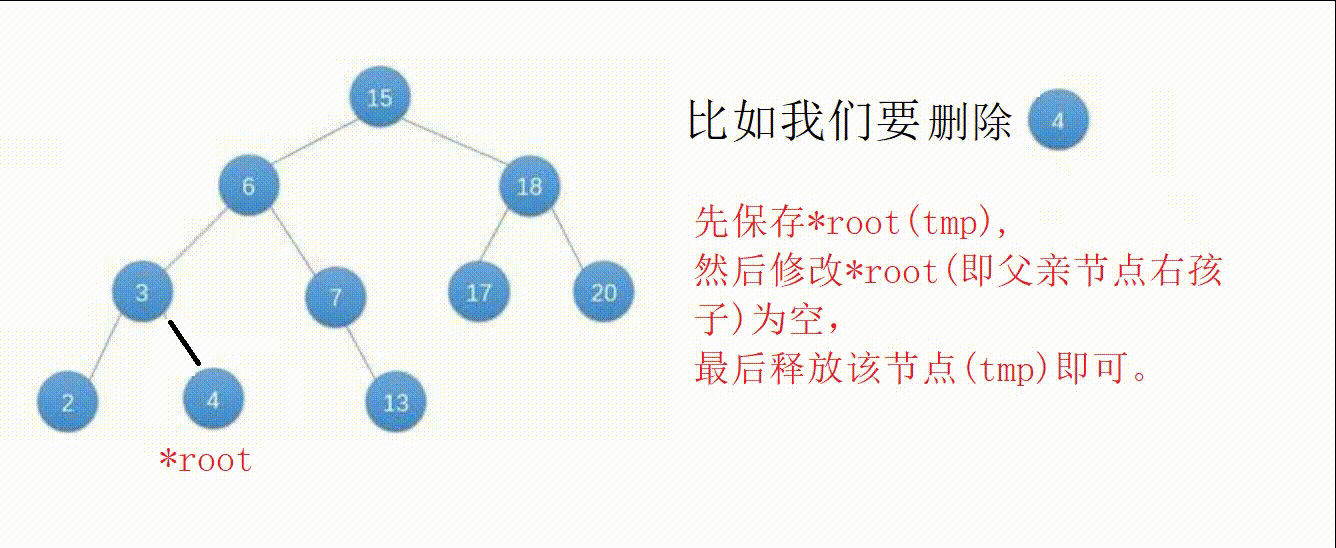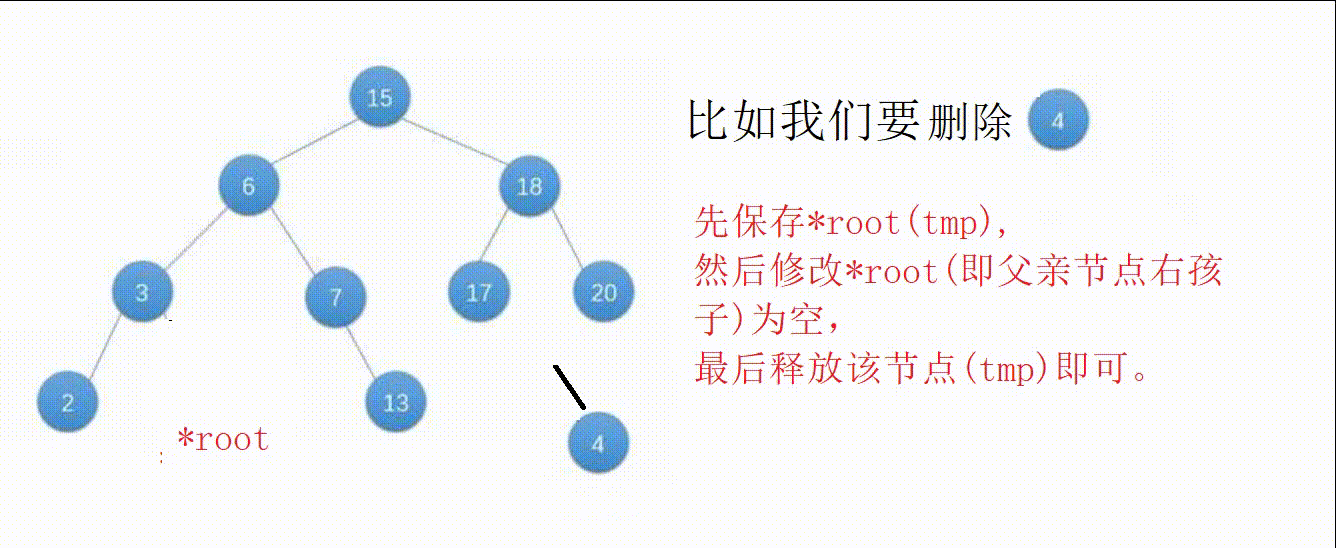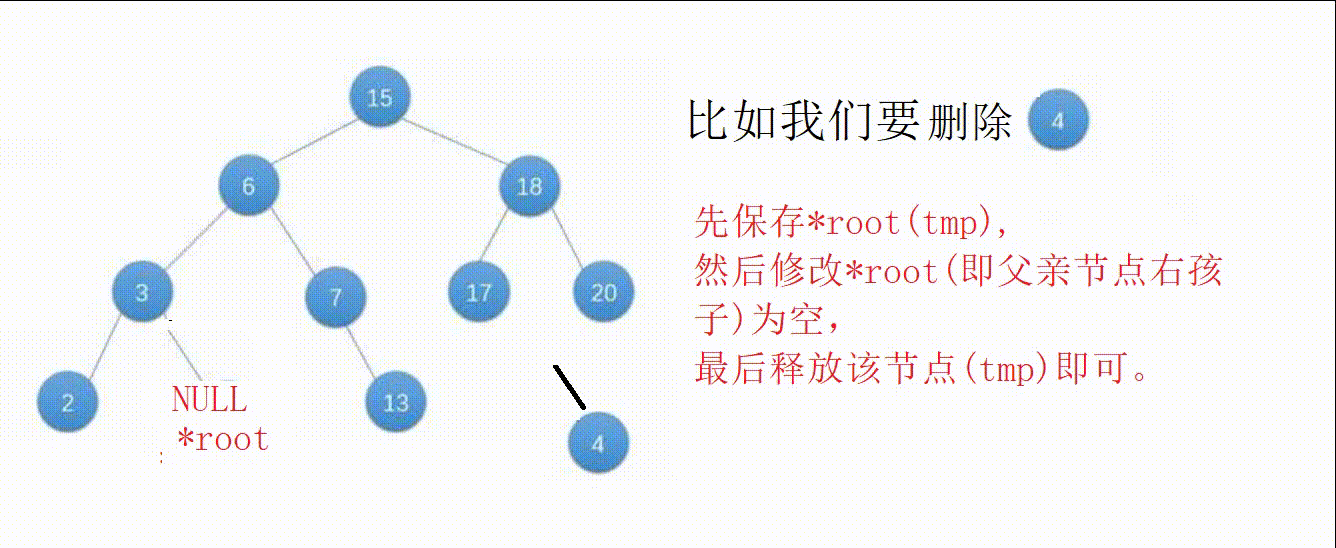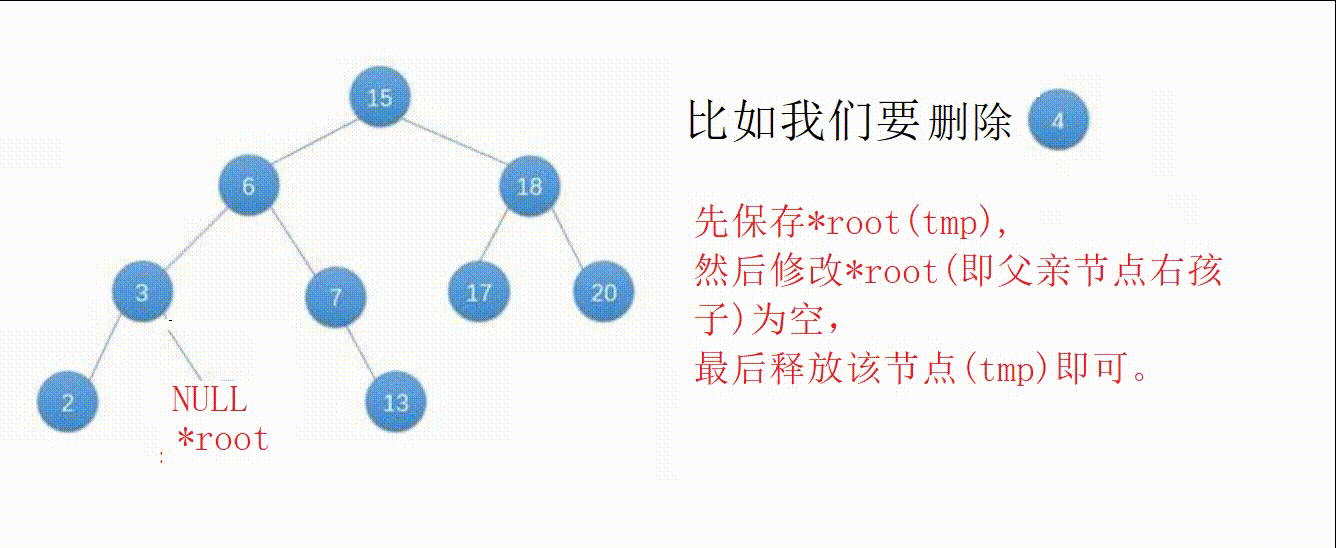
②节点为叶子节点(左右子树都为空)，修改父亲节点的指针域为空后释放该节点即可。

 

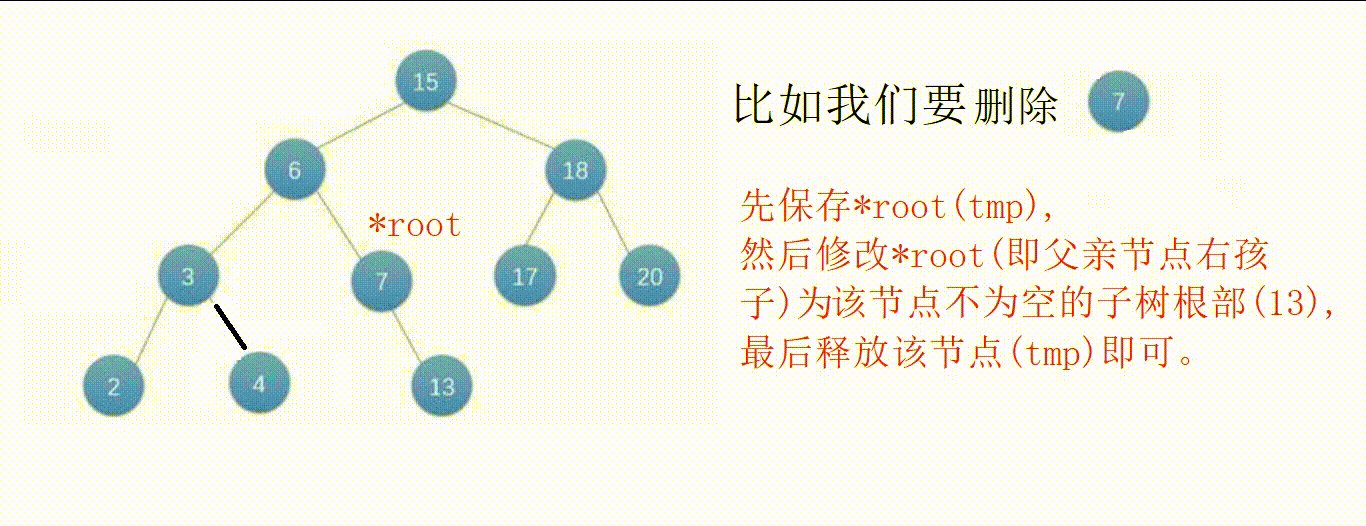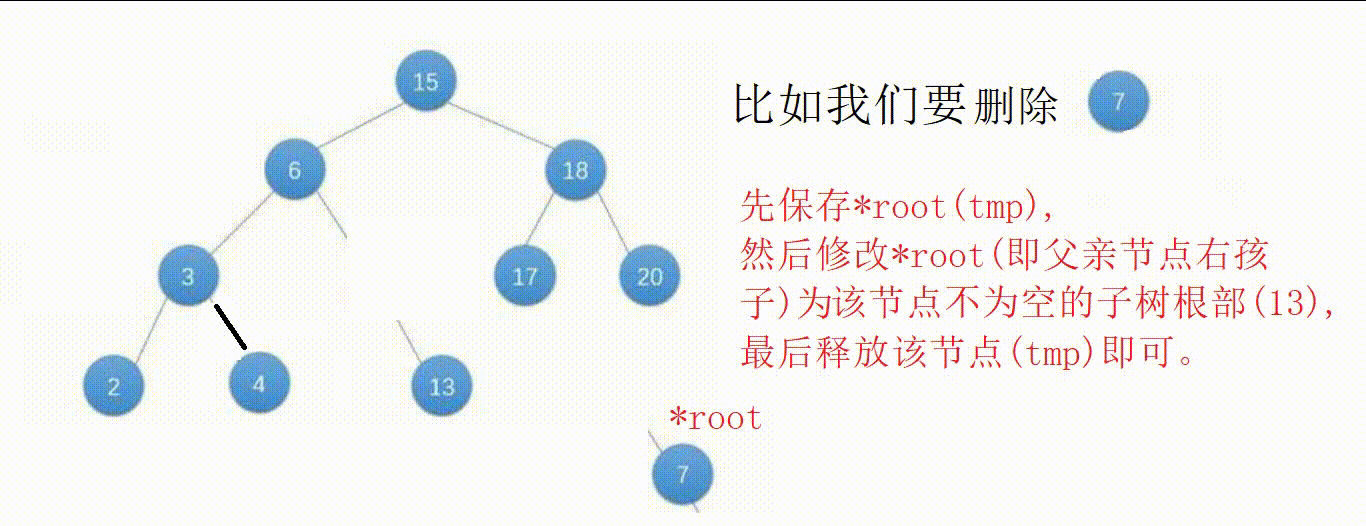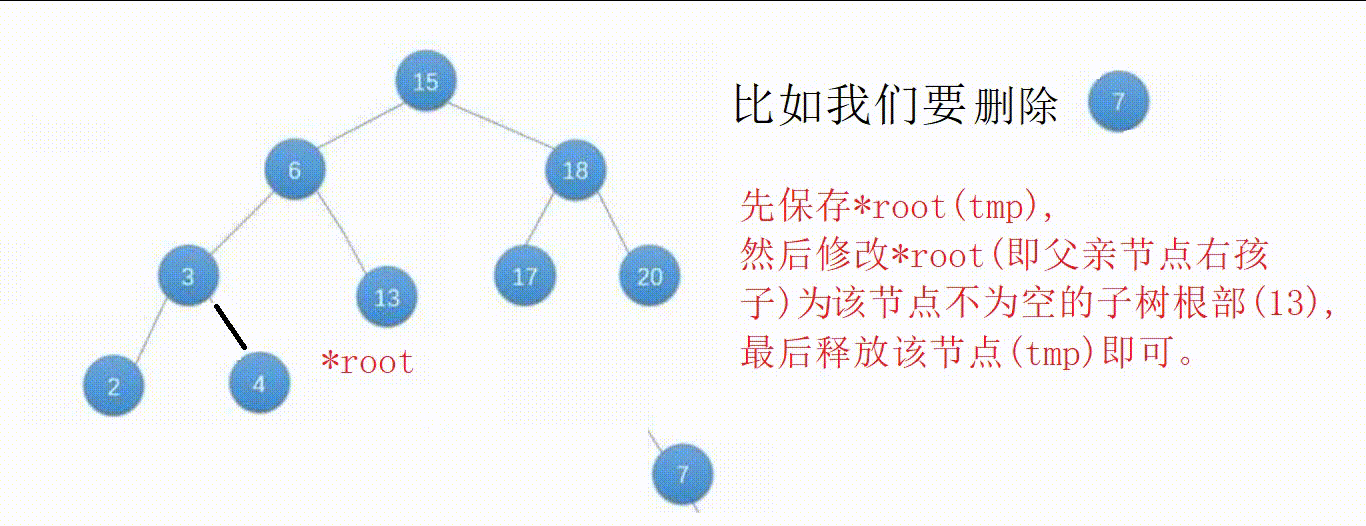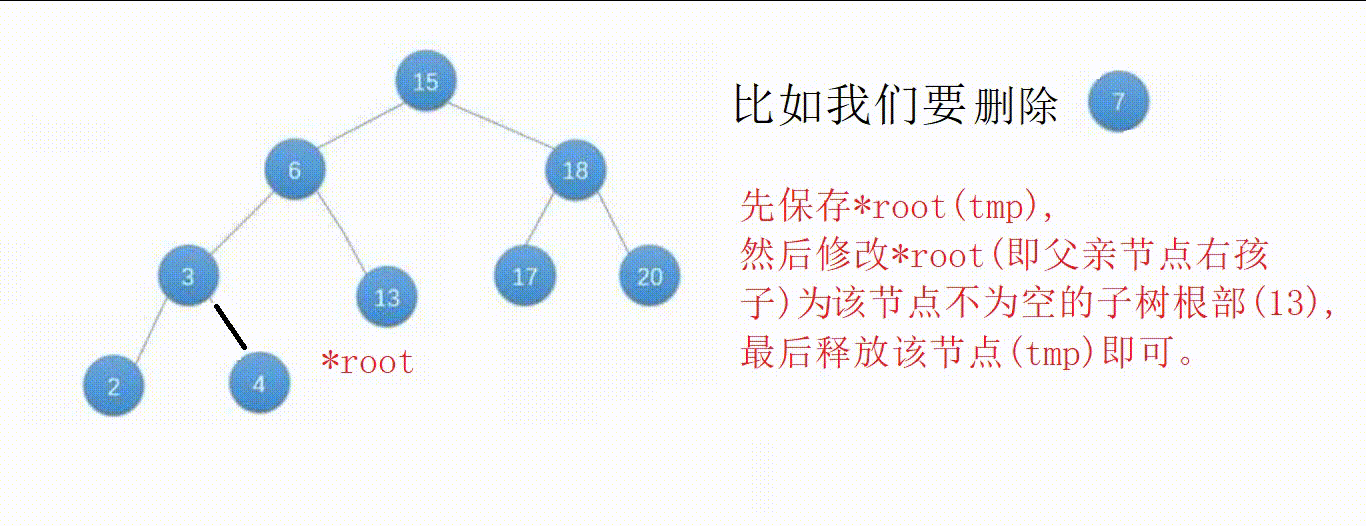
③节点只有左子树或者右子树，另一边为空，修改父亲节点指针域为该节点不为空的子树根部后释放该节点即可。

 

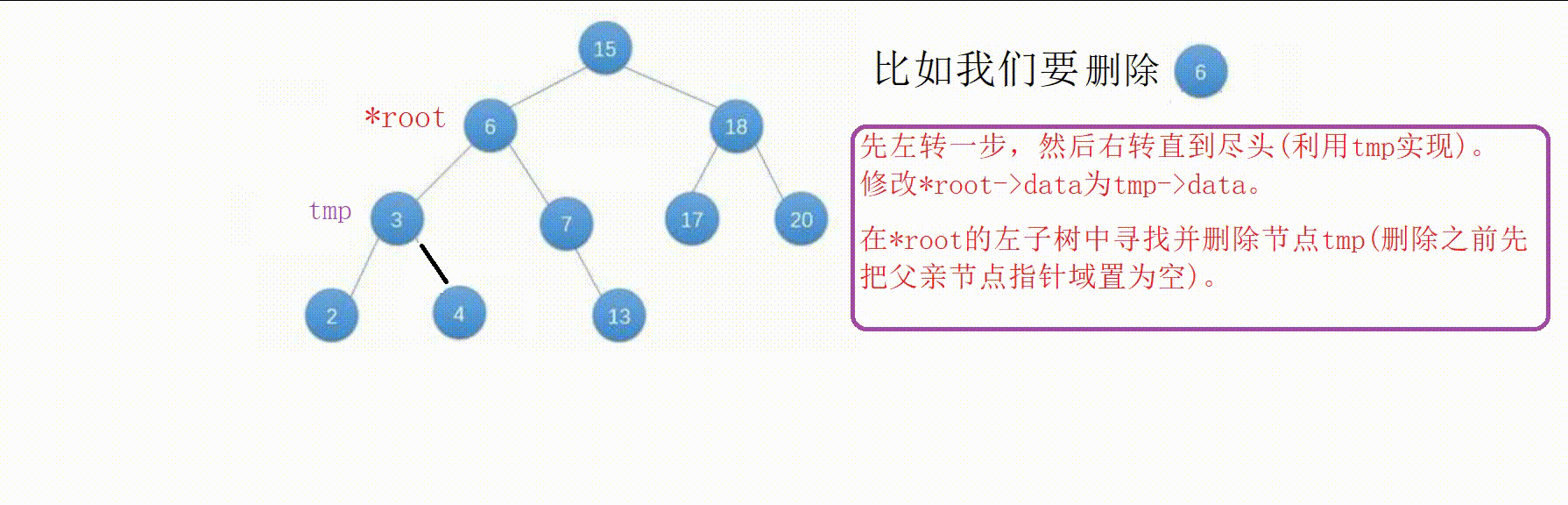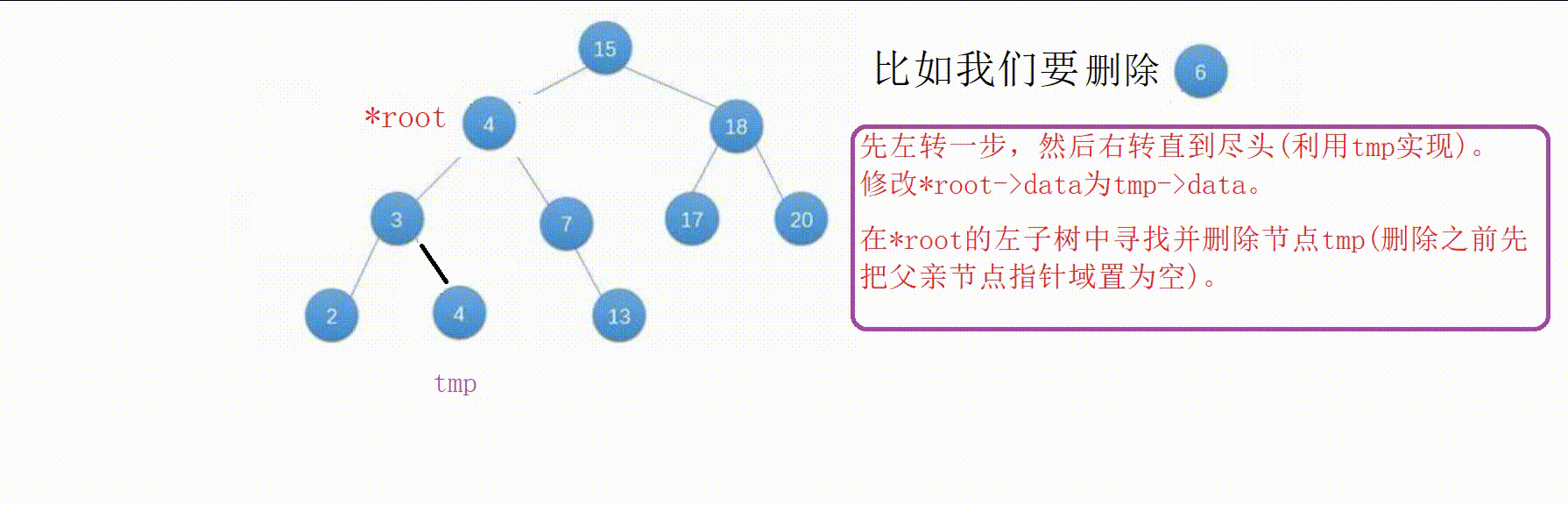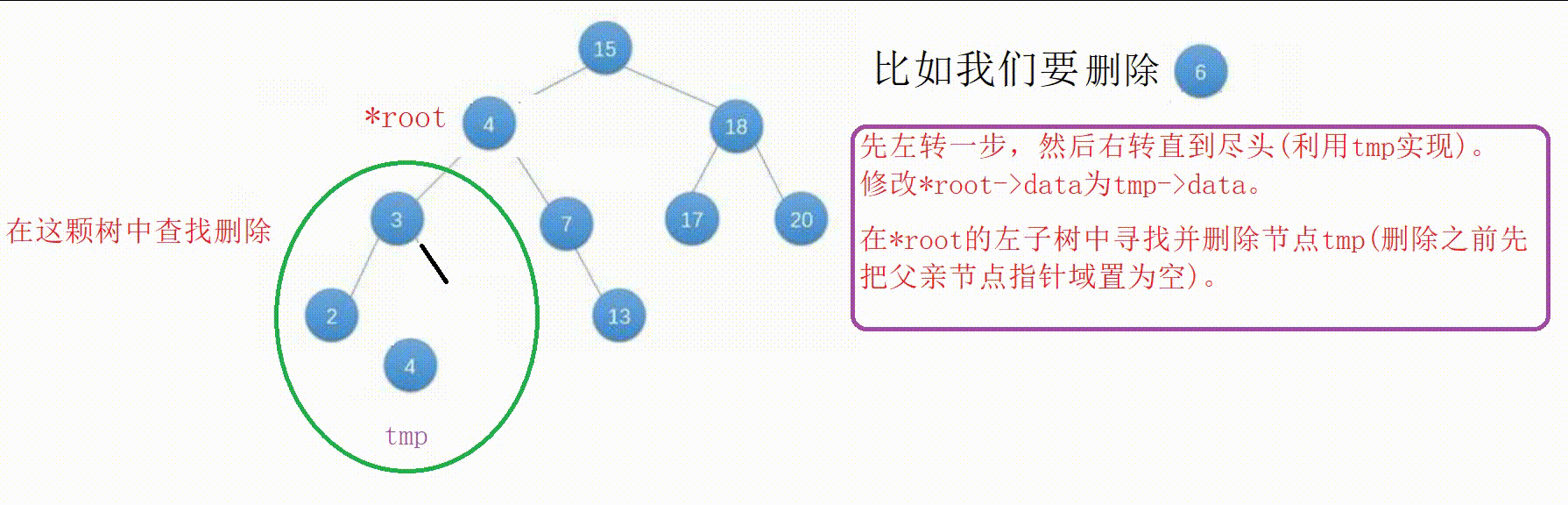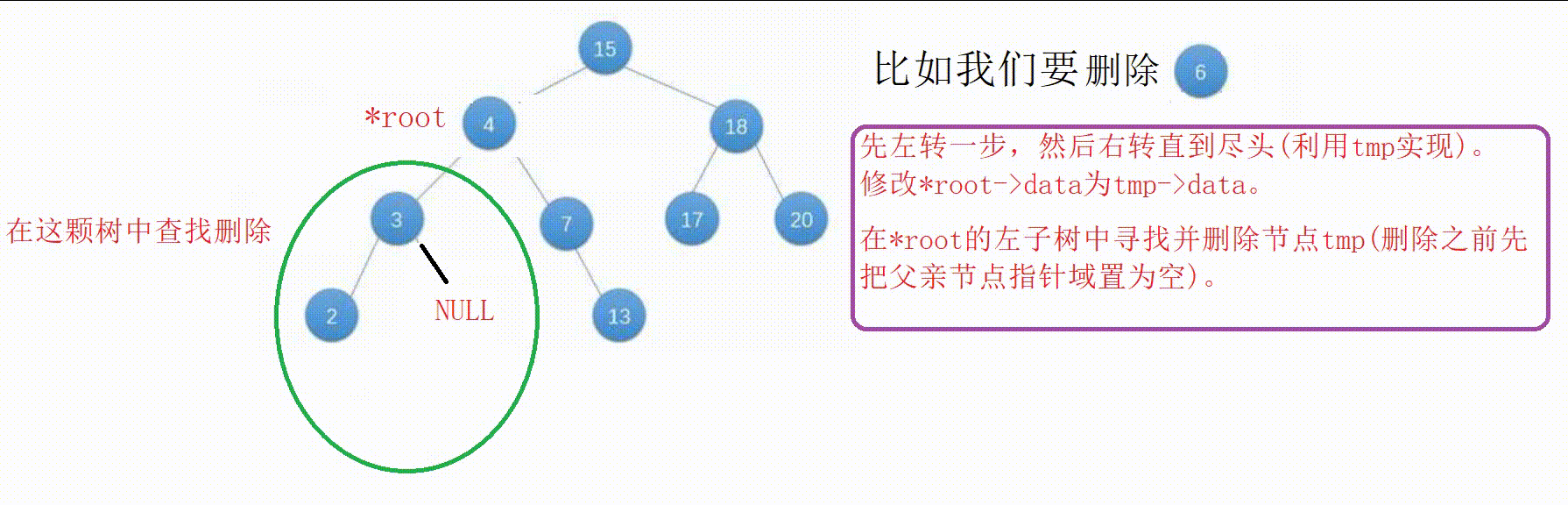
④节点左右子树均不为空。

【1】为了维持搜索树的结构，我们先从该节点(原节点)左转一步，然后一直右转到尽头，这个时候找到的值为左子树中的最大值。

【2】我们把这个值赋值给原节点，将它的父亲节点指针域置空后删除这个节点。

(这个节点要么是叶子节点要么只有一边不为空，可以利用删除函数去递归删除)

【3】这样不仅维持了搜索树的结构(对于任何一个结点，它的左子树中的所有键值都小于它的键值，右子树中的所有键值都大于它的键值)，也达到了删除的效果。

 

代码：

//搜索二叉树删除,删除成功返回0，失败返回-1
//可能改变指针域，传二级
int BSTDelete(BSTNode** root, BSTData x)
{
	//情况①，节点不存在
	if (*root == NULL)
	{
		return -1;
	}

	//找到了
	if ((*root)->data == x)
	{
		BSTNode* tmp = NULL;
		//情况③只有左子树(左右子树都为空的情况②也可以实现)
		if ((*root)->RightChild == NULL)
		{
			tmp = *root;
			//让父亲结点指针域指向待删除结点的左子树
			*root = (*root)->LeftChild;
			free(tmp);
		}
		//情况③只有右子树
		else if ((*root)->LeftChild == NULL)
		{
			tmp = *root;
			//让父亲结点指针域指向待删除结点的右子树
			*root = (*root)->RightChild;
			free(tmp);
		}
		//情况④左右子树都不为空
		else
		{
			tmp = (*root)->LeftChild;
			while (tmp->RightChild != NULL)
			{
				tmp = tmp->RightChild;
			}
			//把最右结点值赋值给现结点
			(*root)->data = tmp->data;
			//递归删除最右结点,在现节点的左子树中找要删除的节点
			BSTDelete(&((*root)->LeftChild), tmp->data);
		}
		return 0;
	}
	//如果x大于现结点值，目标结点在右子树中
	else if (x > (*root)->data)
	{
		return BSTDelete(&(*root)->RightChild, x);
	}
	//如果x小于现结点值，目标结点在左子树中
	else
	{
		return BSTDelete(&(*root)->LeftChild, x);
	}
}

六：全部代码

(1)BinarySearchTree.h(声明)

#pragma once
#include <stdio.h>
#include <stdlib.h>

//重定义数据类型，方便以后更改
typedef int BSTData;

typedef struct BSTNode
{
	//数据域
	BSTData data;
	//指针域，左孩子和右孩子
	struct BSTNode* LeftChild;
	struct BSTNode* RightChild;
}BSTNode;

//搜索二叉树插入,成功返回0，失败返回-1
int BSTInsert(BSTNode** root, BSTData x);

//搜索二叉树遍历(中序)
void InOrder(BSTNode* root);

//搜索二叉树查找,查找到返回结点地址，否则返回空指针
BSTNode* BSTFind(BSTNode* root, BSTData x);

//搜索二叉树删除,删除成功返回0，失败返回-1
int BSTDelete(BSTNode** root, BSTData x);

(2)BinarySearchTree.c(函数具体实现)

#define _CRT_SECURE_NO_WARNINGS 1
#include "BinarySearchTree.h"

//生成一个新结点，很简单
BSTNode* BuyNewNode(BSTData x)
{
	BSTNode* NewNode = (BSTNode*)malloc(sizeof(BSTNode));
	if (NewNode == NULL)
	{
		printf("malloc error\n");
		exit(-1);
	}
	NewNode->LeftChild = NewNode->RightChild = NULL;
	NewNode->data = x;
	return NewNode;
}


//搜索二叉树遍历(中序)
void InOrder(BSTNode* root)
{
	if (root == NULL)
	{
		printf("空 ");
		return;
	}
	InOrder(root->LeftChild);
	printf("%d ", root->data);
	InOrder(root->RightChild);
}


//搜索二叉树插入,成功返回0，失败返回-1
//可能改变指针域，传二级
int BSTInsert(BSTNode** root, BSTData x)
{
	//如果为空，生成一个新结点并链接
	if (*root == NULL)
	{
		BSTNode* NewNode = BuyNewNode(x);
		*root = NewNode;
		return 0;
	}
	//不为空，看是插入右子树中还是左子树中
	//小于插入左子树
	if (x < (*root)->data)
	{
		return BSTInsert(&(*root)->LeftChild, x);
	}
	//大于插入右子树
	else if (x > (*root)->data)
	{
		return BSTInsert(&(*root)->RightChild, x);
	}
	//相等不能插入，返回-1
	else
	{
		return -1;
	}
}


//搜索二叉树查找,查找到返回结点地址，否则返回空指针
BSTNode* BSTFind(BSTNode* root, BSTData x)
{
	//如果这个结点是目标结点或者 
	//已经走到空(未找到返回空)
	if ((root->data == x) || (root == NULL))
	{
		return root;
	}

	//不是就查找子树，比x大在右树中查找，小在左树中查找
	if (x > root->data)
	{
		return BSTFind(root->RightChild, x);
	}
	else
	{
		return BSTFind(root->LeftChild, x);
	}
}


//搜索二叉树删除,删除成功返回0，失败返回-1
//可能改变指针域，传二级
int BSTDelete(BSTNode** root, BSTData x)
{
	//情况①，节点不存在
	if (*root == NULL)
	{
		return -1;
	}

	//找到了
	if ((*root)->data == x)
	{
		BSTNode* tmp = NULL;
		//情况③只有左子树(左右子树都为空的情况②也可以实现)
		if ((*root)->RightChild == NULL)
		{
			tmp = *root;
			//让父亲结点指针域指向待删除结点的左子树
			*root = (*root)->LeftChild;
			free(tmp);
		}
		//情况③只有右子树
		else if ((*root)->LeftChild == NULL)
		{
			tmp = *root;
			//让父亲结点指针域指向待删除结点的右子树
			*root = (*root)->RightChild;
			free(tmp);
		}
		//情况④左右子树都不为空
		else
		{
			tmp = (*root)->LeftChild;
			while (tmp->RightChild != NULL)
			{
				tmp = tmp->RightChild;
			}
			//把最右结点值赋值给现结点
			(*root)->data = tmp->data;
			//递归删除最右结点,在现节点的左子树中找要删除的节点
			BSTDelete(&((*root)->LeftChild), tmp->data);
		}
		return 0;
	}
	//如果x大于现结点值，目标结点在右子树中
	else if (x > (*root)->data)
	{
		return BSTDelete(&(*root)->RightChild, x);
	}
	//如果x小于现结点值，目标结点在左子树中
	else
	{
		return BSTDelete(&(*root)->LeftChild, x);
	}
}

(3)test.c(测试)

#define _CRT_SECURE_NO_WARNINGS 1
#include "BinarySearchTree.h"

void text1()
{
	//一个节点指针，初始化为空
	BSTNode* root = NULL;
	BSTInsert(&root, 15);
	BSTInsert(&root, 6);
	BSTInsert(&root, 18);
	BSTInsert(&root, 3);
	BSTInsert(&root, 7);
	BSTInsert(&root, 17);
	BSTInsert(&root, 20);
	BSTInsert(&root, 2);
	BSTInsert(&root, 4);
	BSTInsert(&root, 13);

	printf("中序遍历>:");
	InOrder(root);

	if (BSTFind(root, 17))
	{
		printf("\n查找成功\n");
	}
		
	if (BSTInsert(&root, 13))
	{
		printf("插入失败\n");
	}

	printf("中序遍历>:");
	InOrder(root);

	if (BSTDelete(&root, 17))
	{
		printf("\n删除失败\n");
	}
	else
	{
		printf("\n删除成功\n");
	}
		
	printf("中序遍历>:");
	InOrder(root);
}

int main()
{
	text1();
	return 0;
}

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/576598.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

mysql 主从同步

mysql 主从同步

① 修改 master 配置文件② 新建同步账号③ 创建数据库④ 修改 slave 配置文件⑤ 配置主从关系⑥ 检验主从结果 角色ipmaster192.168.233.100slave1192.168.233.101slave2192.168.233.102 禁用 selinux 跟 firewal l情况下&#xff1a; ① 修改 master 配置文件 vim /etc/my…
阅读更多...
NEFU linux实验二

NEFU linux实验二

在linux中&#xff0c;家目录又称“home目录”、“主目录”&#xff0c;是用户的宿主目录&#xff0c;通常用来保存用户的文件&#xff0c;可以使用“~”来表示。一个用户登录系统&#xff0c;进入后所处的位置就是“/home”&#xff0c;即家目录&#xff1b;root用户的家目录为…
阅读更多...
路径规划算法：基于鸡群优化的路径规划算法- 附代码

路径规划算法：基于鸡群优化的路径规划算法- 附代码

路径规划算法&#xff1a;基于鸡群优化的路径规划算法- 附代码 文章目录 路径规划算法&#xff1a;基于鸡群优化的路径规划算法- 附代码1.算法原理1.1 环境设定1.2 约束条件1.3 适应度函数 2.算法结果3.MATLAB代码4.参考文献 摘要&#xff1a;本文主要介绍利用智能优化算法鸡群…
阅读更多...
输电线路故障诊断（利用随机森林方法实现二分类和多分类）

输电线路故障诊断（利用随机森林方法实现二分类和多分类）

1.simunlike仿真系统的建立&#xff08; 运行效果 &#xff1a;输电线路故障诊断_哔哩哔哩_bilibili&#xff09; 2.在仿真系统的基础上获取数据集 分别获取单相接地故障、两相接地故障、两相间短路故障、三相接地故障、三相间短路故障和正常状态下的电流&#xff08;Ia,Ib,I…
阅读更多...
一文带你了解MySQL之optimizer trace神器的功效

一文带你了解MySQL之optimizer trace神器的功效

前言&#xff1a; 对于MySQL 5.6以及之前的版本来说&#xff0c;查询优化器就像是一个黑盒子一样&#xff0c;你只能通过EXPLAIN语句查看到最后优化器决定使用的执行计划&#xff0c;却无法知道它为什么做这个决策。这对于一部分喜欢刨根问底的小伙伴来说简直是灾难&#xff1…
阅读更多...
2023年5月14日蓝桥杯c++省赛中级组

2023年5月14日蓝桥杯c++省赛中级组

选择题讲解 1.）C++中，bool类型的变量占用字节数为 ( )。 A.1B.2 C.3 D.4 答案：A 解析：（C++ 中 bool 类型与 char 类型一样，都需要1 byte。一些其他类型的占用字节数：short：2 byte。int：4 byte。long long：8 byte。double：8 byte。） 2.）以下关于C++结构体的说…
阅读更多...
代码随想录二刷 day04 | 链表之 24两两交换链表中的节点 19删除链表的倒数第N个节点 面试题 02.07. 链表相交 142.环形链表II

代码随想录二刷 day04 | 链表之 24两两交换链表中的节点 19删除链表的倒数第N个节点 面试题 02.07. 链表相交 142.环形链表II

24. 两两交换链表中的节点 题目链接 解题思路&#xff1a; 先将一些可能会改变的节点保存一下&#xff0c;然后再按照三个步骤就行修改 注意 要使用改变以后节点的指针&#xff08;这个地方一刷的时候没注意到&#xff0c;稀里糊涂的过去了&#xff09; 代码如下&#xff1a;…
阅读更多...
【八股】计算机网络-HTTP和HTTPS的区别、HTTPS加密传输原理

【八股】计算机网络-HTTP和HTTPS的区别、HTTPS加密传输原理

计算机网络-HTTP和HTTPS的区别、HTTPS加密传输原理 一、HTTP和HTTPS的基本概念二、HTTP与HTTPS的区别三、HTTPS加密传输原理1. 什么是HTTPS1.1 https诞生的原因1.2 https加密方式1.3.http和https的区别 2. https的工作流程3. 数字证书3.1 什么是数字证书3.2 如何申请数字证书3.…
阅读更多...
亚马逊六页纸沟通法，拒绝PPT

亚马逊六页纸沟通法，拒绝PPT

亚马逊六页纸沟通管理法&#xff0c;拒绝PPT 使用一种简洁的「结构化备忘录」 内部管理会议沟通&#xff0c;每次不超过六页 趣讲大白话&#xff1a;让沟通更有效 【趣讲信息科技178期】 **************************** 那么“6页备忘录”到底是什么呢&#xff1f; 1. What we d…
阅读更多...
供应链 | 在线平台的研究与思考（一）：销售渠道与模式选择

供应链 | 在线平台的研究与思考（一）：销售渠道与模式选择

封面图来源&#xff1a; https://www.pexels.com/zh-cn/photo/4968391/ 编者按 当前&#xff0c;电商平台主要采用两种销售模式&#xff1a;代理和分销。商家根据自身情况选择线上或线下渠道&#xff0c;而电商平台会根据不同的线上商家选择适当的分销模式。本期编者精选的两…
阅读更多...
Unity 工具 之 Azure 微软语音合成普通方式和流式获取音频数据的简单整理

Unity 工具 之 Azure 微软语音合成普通方式和流式获取音频数据的简单整理

Unity 工具 之 Azure 微软语音合成普通方式和流式获取音频数据的简单整理 目录 Unity 工具 之 Azure 微软语音合成普通方式和流式获取音频数据的简单整理 一、简单介绍 二、实现原理 三、注意实现 四、实现步骤 六、关键脚本 一、简单介绍 Unity 工具类&#xff0c;自己整…
阅读更多...
从事黑客工作十余年，究竟如何成为一名高级的安全工程师？

从事黑客工作十余年，究竟如何成为一名高级的安全工程师？

目录 1. 前言 2. 经验 3. 要考虑的问题 4. 学习路线详解 第一步&#xff1a;计算机基础 第二步&#xff1a;编程能力 第三步&#xff1a;安全初体验 第四步&#xff1a;分方向 尾言 参考书籍列表 1. 前言 说实话&#xff0c;一直到现在&#xff0c;我都认为绝大多数…
阅读更多...
STP协议

STP协议

目录 STP的基本概念&#xff1a; 桥ID&#xff08;Bridge ID&#xff09;&#xff1a; 根桥&#xff1a; 开销&#xff08;Cost&#xff09;&#xff1a; RPC&#xff08;根路径开销&#xff09;&#xff1a; Port ID&#xff1a; BPDU&#xff1a;&#xff08;网桥协议…
阅读更多...
ROS：ROS是什么

ROS：ROS是什么

目录 一、ROS简介二、ROS可以做些什么三、ROS特征四、ROS特点4.1点对点设计4.2不依赖编程语言4.3精简与集成4.4便于测试4.5开源4.6强大的库与社区 五、ROS的发展六、ROS架构6.1OS层6.2中间层6.3应用层 七、通信机制八、计算图8.1节点&#xff08;Node&#xff09;8.2节点管理器…
阅读更多...
当ChatGPT参加中国高考，把全国A卷B卷喂给它后，竟严重偏科

当ChatGPT参加中国高考，把全国A卷B卷喂给它后，竟严重偏科

作者 |Python ChatGPT作为一个智能人机对话应用&#xff0c;在推出后迅速风靡全球。仅仅一个月的时间&#xff0c;其用户数量已经突破了一亿大关。人们也用ChatGPT测试了很多考试项目&#xff0c;例如SAT、AP、GRE等。然而&#xff0c;如果让ChatGPT来参加我们中国的高考&…
阅读更多...
Jetson Orin Nano 快速安装 ROS2 Foxy详解

Jetson Orin Nano 快速安装 ROS2 Foxy详解

大家好&#xff0c;我是虎哥&#xff0c;入手一块Jeston Orin nano 8G模块&#xff0c;这个模块因为是英伟达未来5年左右主推的模块&#xff0c;所以我逐步会将之前所有的应用都在这个模块环境上做适配&#xff0c;本章内容&#xff0c;我将主要围绕安装ROS2 Foxy版本为主展开。…
阅读更多...
探索Java面向对象编程的奇妙世界(四)

探索Java面向对象编程的奇妙世界(四)

⭐ 变量的分类和作用域⭐ 包机制(package、import)⭐ 面向对象三大特征——继承⭐ 继承的作用⭐ 继承的实现⭐ instanceof 运算符⭐ 继承使用要点⭐ 方法重写 override⭐ final 关键字⭐ 继承和组合 ⭐ 变量的分类和作用域 变量有三种类型&#xff1a;局部变量、成员变量(也称为…
阅读更多...
Diffusion Model 深入剖析

Diffusion Model 深入剖析

Diffusion Model 深入剖析 最近AI生成艺术领域非常火热&#xff0c;从 Midjourney 到 Stable Diffusion&#xff0c;不管你是绘画高手还是艺术小白&#xff0c;只要输入想要绘制内容的描述或者基础图像&#xff0c;就可以生成富有艺术感的画作&#xff01; 这些风格各异、以假…
阅读更多...
CodeForces..构建美丽数组.[简单].[情况判断].[特殊条件下的最小值奇偶问题]

CodeForces..构建美丽数组.[简单].[情况判断].[特殊条件下的最小值奇偶问题]

题目描述&#xff1a; 题目解读&#xff1a; 给定数组a[n]&#xff0c;ai>0&#xff0c;问能否得到一个数组b[n]&#xff0c;数组b中的元素都大于0且全奇or全偶。 数组b中的元素biai or ai-aj&#xff08;1<j<n&#xff09;。 解题思路&#xff1a; 数组b中的元素都…
阅读更多...
IDEA代码替换

IDEA代码替换

IDEA代码替换 快捷键 当前文件内容 C t r l R CtrlR CtrlR 全局替换 C t r l S h i f t R CtrlShiftR CtrlShiftR 使用 第一行输入栏&#xff1a;输入被替换内容 第二行输入栏&#xff1a;输入替换内容 详细使用 第一行输入栏后第一个图标&#xff1a;换行 第一行输…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023