1143.最长公共子序列

教程视频：https://www.bilibili.com/video/BV1ye4y1L7CQ
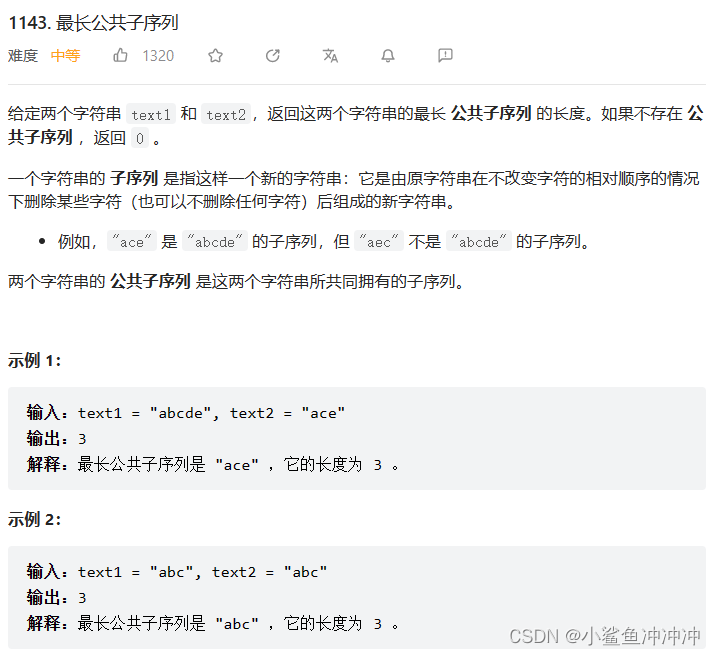
在这里插入图片描述

解法一：动态规划

思路：
1、dp[i][j]含义：表示以text1从0 ~ i-1个字符和text2从0 ~ j-1个字符之间最长公共子序列的长度。
2、递归公式：当前会有两种状况：
a. text1.charAt(i-1)==text2.charAt(j-1)，相同则dp[i][j]=dp[i-1][j-1]+1;
b. text1.charAt(i-1)!=text2.charAt(j-1)，不相同则比较从哪边获得的长度最大：dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
3、dp初始化：dp[i][0]和dp[0][j]没有实际意义，为保证递归，全部初始化为0
4、遍历顺序：外层遍历text1，内层遍历text2
5、打印验证。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp =new int[text1.length()+1][text2.length()+1];
        int maxLength = 0;
        for(int i=1;i<=text1.length();i++){
            for(int j=1;j<=text2.length();j++){
                if(text1.charAt(i-1)==text2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
                }
                maxLength=Math.max(maxLength,dp[i][j]);
            }
        }
        return maxLength;
    }
}

1035.不相交的线

教程视频：https://www.bilibili.com/video/BV1h84y1x7MP
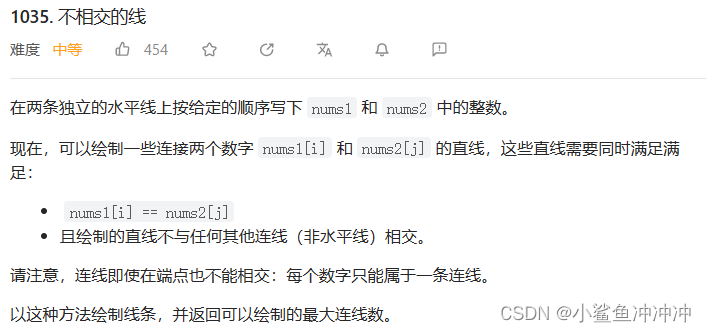
在这里插入图片描述

解法一：动态规划

思路：（本题同上一题【1143.最长公共子序列】）
1、dp[i][j]含义：表示以nums1从0 ~ i-1和nums2从0 ~ j-1范围之间最长公共子序列的长度。
2、递归公式：当前会有两种状况：
a. nums1[i - 1] 与 nums2[j - 1]相同，相同则dp[i][j]=dp[i-1][j-1]+1;
b. nums1[i - 1] 与 nums2[j - 1]不相同，不相同则比较从哪边获得的长度最大：dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
3、dp初始化：dp[i][0]和dp[0][j]没有实际意义，为保证递归，全部初始化为0
4、遍历顺序：外层遍历text1，内层遍历text2

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length+1][nums2.length+1];
        int maxLength = 0;
        for(int i=1;i<=nums1.length;i++){
            for(int j=1;j<=nums2.length;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
                }
                maxLength=Math.max(maxLength,dp[i][j]);
            }
        }
        return maxLength;
    }
}

53. 最大子序和动态规划

教程视频：https://www.bilibili.com/video/BV19V4y1F7b5
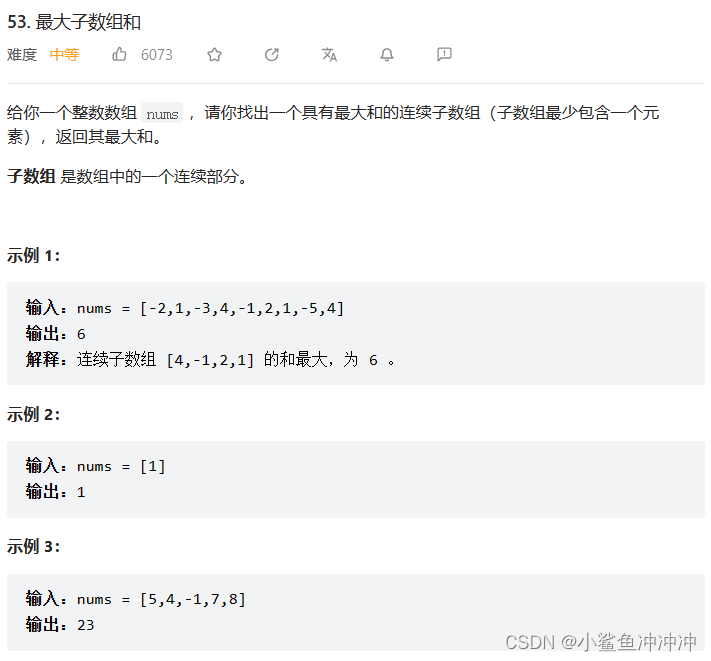
在这里插入图片描述

解法一：动态规划

思路：
1、dp[i]含义：以nums[i-1]为结尾的最大连续子数组和。
2、递归公式：dp[i]=nums[i-1]+Math.max(dp[i-1], 0);
3、dp初始化：dp[0]没有实际意义，为保证递归，初始化为0，其余索引值都会在递归时被覆盖无需考虑。由于数组和可能是负数，需要将maxSum初始化为Integer.MIN_VALUE
4、遍历顺序：正向遍历
5、打印验证。

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp =new int[nums.length+1];
        int maxSum=Integer.MIN_VALUE;
        for(int i=1;i<=nums.length;i++){
            dp[i]=nums[i-1]+Math.max(dp[i-1],0);
            maxSum=Math.max(maxSum,dp[i]);
        }
        return maxSum;
    }
}