昨天一位邻居在群里问了一道题目：

已知：如图，OA平分∠BAC，∠1=∠2．
求证：△ABC是等腰三角形．

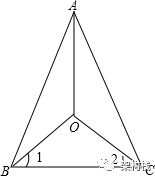
先不讲如何来解答这个题目，重点是我们来分析这道题到底在考察什么，如果条件换成AB=AC，证明OA平分∠BAC，那么就重点看等腰三角形的特性，但是这里反过来证明AB=AC，那么就要把突破口放在角平分线上面。下面我们来梳理一下角平分线的几个模型：

【模型】一、角平分线垂两边 角平分线+外垂直 

当已知条件中出现OP 为△OAB 的角平分线、 PM⊥OA于点 M时，辅助线的作法大都为过点P作PN⊥OB 即可.即有 PM ⊥ PN 、 △OMP ≌ △ONP 等，利用相关结论解决问题. 

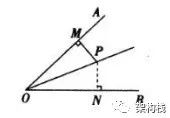
【模型】二、角平分线垂中间 角平分线+内垂直 

当已知条件中出现OP 为△AOB 的角平分线, PM⊥OP 于点 P 时，辅助线的作法大都为延长MP交OB 于点 N 即可.即有 △OMN 是等腰三角形、OP 是三线等。

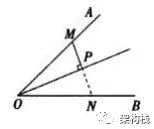
【模型】三、角平分线构造轴对称 角平分线+截线段等 

当 已知 条件中出现OP 为AOB 的角平分线、PM不具备特殊位置时，辅助线的作法大都为在OB上截取ON  OM ，连结 PN 即可.即有 △OMP ≌ △ONP 

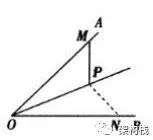
【模型】四、角平分线加平行线等腰现角平分线+平行线

当已知条件中出现OP 为∠AOB 的角平分线，点 P 角平分线上任一点时，辅助线的作法大都为过点P作 PM //OB 或 PM //OA即可.即有 △OMP 是等腰三角形。

有了这四个模型，我们就有了以下多种解题思路，这里先列2个方案：

如果我们考虑模型一，那么解题思路如下：

证明：作OE⊥AB于E，OF⊥AC于F，

∵AO平分∠BAC，

∴OE=OF

∵∠1=∠2，

∴OB=OC．

∴Rt△OBE≌Rt△OCF．

∴∠ABO=∠ACO．

∴∠1+∠ABO=∠2+∠ACO．

即∠ABC=∠ACB．

∴AB=AC．

∴△ABC是等腰三角形．

如果我们考虑模型三，那么解题思路如下：

如果AB≠AC, 不失一般性，假设AB<AC, 于是在AC上取一点D，让AB=AD,

由于∠BAO=∠DAO, 利用三角形全等S.A.S判定方法，可以得到△ABO≌△ADO, 

∴OB=OD，

∵∠1=∠2，

∴OB=OC，进而得到OD=OC，由于∠AOD在锐角△ABC内部，∴∠AOD>90°，进而可以得到∠ODC>90°，这与OD=OC矛盾

∴AB=AC，△ABC是等腰三角形。

同样的，我们也可以按照模型二和模型四完成这道题的解决，如果感兴趣的朋友，可以自行完成。

因此，摸清楚底层的几何模型，才是解题举一反三的关键。