强连通分量(SCC, Strongly Connected Component)
- 强连通分量的概念
- 强连通分量的应用
- 强连通分量的算法——Tarjan算法
强连通分量的概念
在有向图中,任意两个顶点 v i v_i vi 和 v j v_j vj 互相可达(也即存在路径 v i → v j v_i \rightarrow v_j vi→vj 和路径 v j → v i v_j \rightarrow v_i vj→vi),则称这些顶点构成连通分量。
强连通分量(SCC, Strongly Connected Component),即极大连通分量,对于一个联通分量,如果每个包含它的极大联通分量就是其本身,则称为极大联通分量。或者说强连通分量只要增加一个顶点,则无法构成连通分量。

例如在上图中,BCDE构成强连通分量,而CD则不是强连通分量。
强连通分量的应用
将有向图中的强连通分量缩成一个顶点,有向图则成为一个有向五环图(DAG),而DAG也称为拓扑图,其顶点可以进行拓扑排序。

而拓扑图在图论中可以用于求解最短/长路径。拓扑图在优化编译器中也有重要应用。
强连通分量的算法——Tarjan算法
比较典型的算法是Tarjan算法,该算法时间复杂度为 O(V+E)。下面介绍下该算法原理,参考了youtube一位大佬的视频。
Tarjan算法主体采用DFS遍历,每访问一个顶点,给该顶点赋值一个id和low-link,low-link表示当前顶点能到达的顶点中最小的id(包括它自己的id)。

可见low-link相同的节点就组成强联通分量。该算法核心就是计算每个节点low-link值。
该算法需要维护一个栈,防止跨Sccs跟新low-link,也就是说在有效的顶点范围内更新low-link。
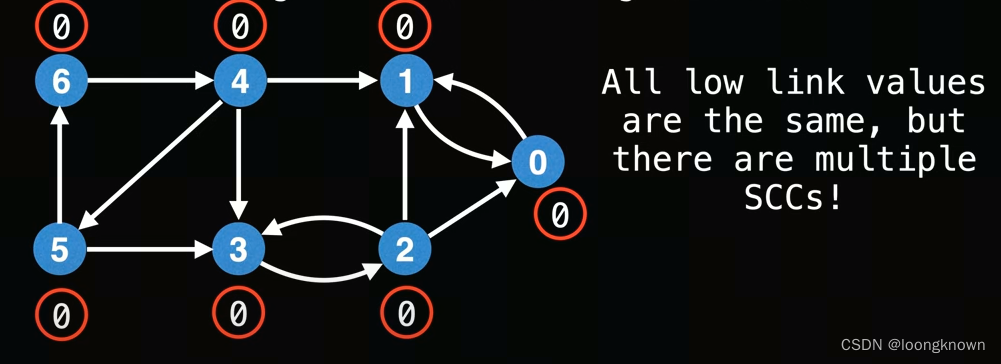
DFS访问一个未访问的顶点即加入栈中作为有效顶点,当找到一个Scc时,将这些顶点从栈中弹出。
low-link的更新条件为:使用节点v的low-link更新顶点u的low-link,必须有一个从u到v的边,并且顶点v必须在栈中。
Tarjan算法概览:
- 标记所有节点为未访问状态(unvisited)。
- 开始DFS,访问节点,并为其分配id和low-link值,标记该顶点已经访问过(visited),并加入到栈中。
- 当DFS回溯时,如果先前节点在栈中,则使用当前顶点的前一个顶点来更新当前顶点的low-link(取二者最小值)。
- 在完成当前顶点的所有邻居后,如果以当前顶点为起始的顶点组成Sccs,则将栈中的顶点弹出,直到当前顶点。
例如:

任意选择顶点开始DFS,这里选择的是顶点0,依次将顶点0、1、2入栈,当顶点2继续DFS时,发现顶点0已经访问过了,于是开始回溯,并更新计算low-link值。当回溯到顶点0时,其id值等于low-link值,说明找到了一个Scc,此时将相关顶点弹出。
然后再选择一个顶点继续DFS,这里选择顶点3。

将顶点3、4、5依次入栈,从顶点5继续DFS,访问顶点0,顶点已经访问过了,则回溯到顶点5,此时不更新low-link,因为顶点0不在栈中。接着继续DFS到顶点6和4,将顶点6和4入栈(顶点2和顶点0的情况一样),顶点4已经访问过了,开始回溯,并更新low-link值。当回溯到顶点4时,其id值和low-link值相等,找到一个Scc,依次将顶点6、5、4弹出。

此时栈中还剩顶点3,继续DFS到顶点4,节点4已经访问过了,回溯到顶点3,顶点4不在栈中,不更新顶点3的low-link。此时虽然顶点3的id和low-link相等,但顶点3的邻居还没访问完,继续DFS到顶点7。

同样地,找到一个新的Scc。
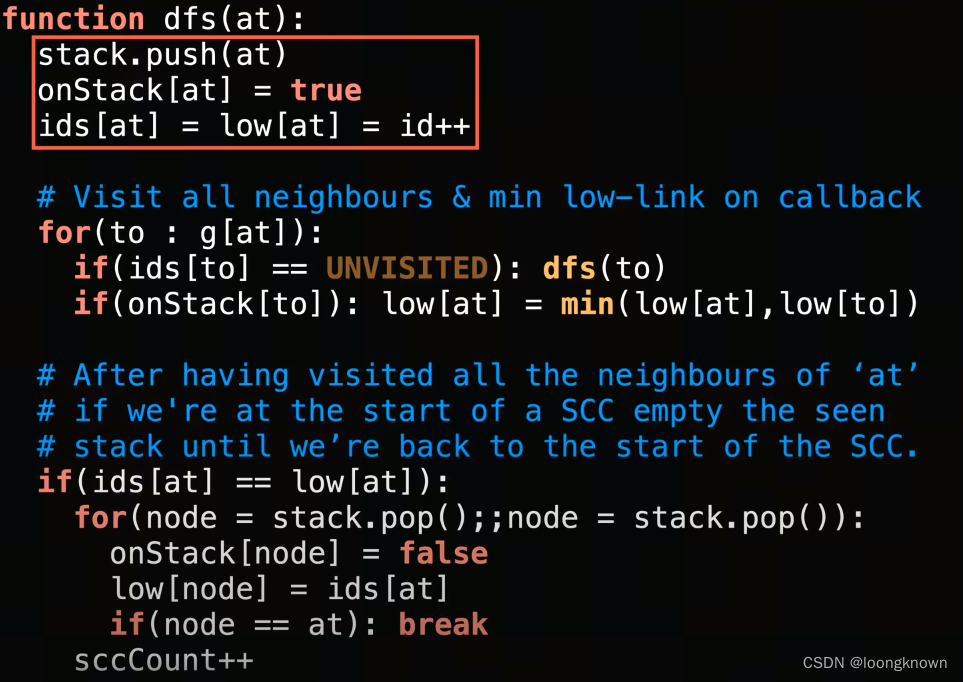
最后,给出完整的为伪代码:

参考:
- https://www.youtube.com/watch?v=wUgWX0nc4NY
- https://github.com/williamfiset/Algorithms