1. 作者介绍

唐杰，男，西安工程大学电子信息学院，2022级研究生
研究方向：机器视觉与人工智能
电子邮件：3225033259@qq.com

陈梦丹，女，西安工程大学电子信息学院，2022级硕士研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：1169738496@qq.com

2. LDA降维算法

2.1 基本概念

线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同，LDA是一种监督学习的降维技术，数据集的每个样本有类别输出。

LDA分类思想：多维空间中，数据处理分类问题较为复杂，LDA算法将多维空间中的数据投影到一条直线上，将d维数据转化成1维数据进行处理。对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离。对数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别。

如果用一句话概括LDA思想，即“投影后类内方差最小，类间方差最大”。

2.2 算法流程

LDA算法流程如下：
在这里插入图片描述

3. LDA算法实现

3.1 数据集介绍

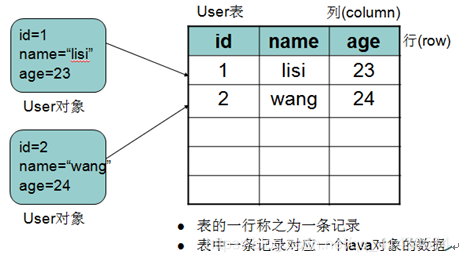
Iris数据集的中文名是安德森鸢尾花卉数据集，英文全称是Anderson’s Iris data set。Iris包含150个样本，对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息，所以Iris数据集是一个150行5列的二维表。

通俗地说，Iris数据集是用来给花做分类的数据集，每个样本包含了花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征（前4列），我们需要建立一个分类器，分类器可以通过样本的四个特征来判断样本属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾（这三个名词都是花的品种）。

Iris的每个样本都包含了品种信息，即目标属性（第5列，也叫target或label）。如下所示：
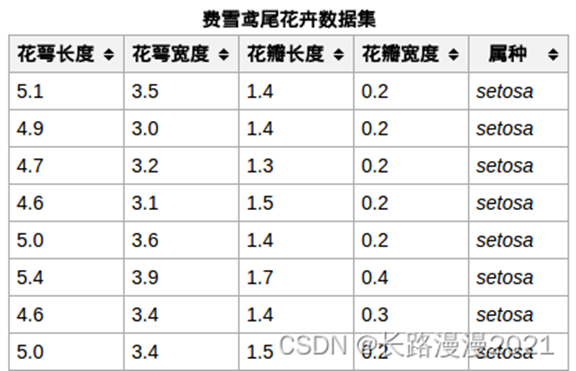
在这里插入图片描述

3.2 代码实现

import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# 定义LDA类
class LDA:
    def __init__(self, n_components=2, kernel='rbf', gamma=400):
      self.n_components = n_components
      self.kernel = kernel
      self.gamma = gamma
    def fit(self, X, y):
      # 计算内部和外部类别散度矩阵
      X_mean = np.mean(X, axis=0)
      S_W = np.zeros((X.shape[1], X.shape[1]))
      S_B = np.zeros((X.shape[1], X.shape[1]))
      for i in range(3):
         X_class = X[y == i, :]
         X_class_mean = np.mean(X_class, axis=0)
         S_W += np.dot((X_class - X_class_mean).T, (X_class - X_class_mean))
         S_B += len(X_class) * np.dot((X_class_mean - X_mean).reshape(-1, 1), (X_class_mean - X_mean).reshape(1, -1))
      # 使用LDA算法计算投影矩阵W
      eig_val, eig_vec = np.linalg.eig(np.dot(np.linalg.inv(S_W), S_B))
      idx = np.argsort(-eig_val.real)
      self.W = eig_vec[:, idx[:self.n_components]]
      # 归一化处理
      scaler = MinMaxScaler()
      self.W = scaler.fit_transform(self.W)
    def transform(self, X):
      # 投影到特征空间
      X_new = np.dot(X, self.W)
      # 归一化处理
      scaler = MinMaxScaler()
      X_new = scaler.fit_transform(X_new)
      return X_new
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 模型训练
lda = LDA(n_components=2, kernel='rbf')
lda.fit(X, y)
# 数据转换
X_new = lda.transform(X)
# 可视化降维后的数据分布
plt.scatter(X_new[:, 0], X_new[:, 1], c=y)