香农-范诺编码

简介

香农-范诺编码（Shannon–Fano Coding）是一种基于一组符号集及其出现的或然率（估量或测量所得），从而构建前缀码的技术。
一般过程：符号从最大可能到最少可能排序，将排列好的信源符号分化为两大组，使两组的概率和近于相同，并各赋予一个二元码符号0和1。只要有符号剩余，以同样的过程重复这些集合以此确定这些代码的连续编码数字。依次下去，直至每一组的只剩下一个信源符号为止。当一组已经降低到一个符号，显然，这意味着符号的代码是完整的，不会形成任何其他符号的代码前缀。

算法

Shannon-Fano的树是根据旨在定义一个有效的代码表的规范而建立的。实际的算法很简单：

1. 对于一个给定的符号列表，制定了概率相应的列表或频率计数，使每个符号的相对发生频率是已知。
2. 排序根据频率的符号列表，最常出现的符号在左边，最少出现的符号在右边。
3. 清单分为两部分，使左边部分的总频率和尽可能接近右边部分的总频率和。
4. 该列表的左半边分配二进制数字0，右半边是分配的数字1。这意味着，在第一半符号代都是将所有从0开始，第二半的代码都从1开始。
5. 对左、右半部分递归应用步骤3和4，细分群体，并添加位的代码，直到每个符号已成为一个相应的代码树的叶。

示例

五个可被编码的字母有如下出现次数：

符号	A	B	C	D	E
计数	15	7	6	6	5
概率	0.38461538	0.17948718	0.15384615	0.15384615	0.12820513

从左到右，所有的符号以它们出现的次数划分。在字母B与C之间划定分割线，得到了左右两组，总次数分别为22，17。这样就把两组的差别降到最小。通过这样的分割, A与B同时拥有了一个以0为开头的码字, C，D，E的码子则为1。随后，在树的左半边，于A，B间建立新的分割线，这样A就成为了码字为00的叶子节点，B的码字为01。经过四次分割，得到了一个树形编码。

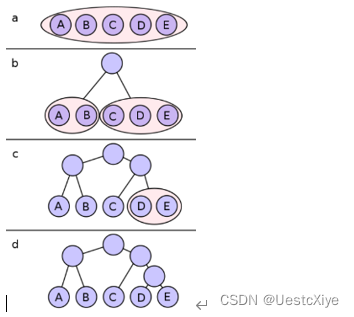
在最终得到的树中，拥有最大频率的符号被两位编码，其他两个频率较低的符号被三位编码。

符号	A	B	C	D	E
编码	00	01	10	110	111

最终的平均码字长度（平均比特率）=((15+7+6)*2bit+(6+5)*3bit)/39=2.28bit。