1 TreeMap的特点
概念:
TreeMap是一个双列集合,是Map的子类。底层由红黑树结构构成。
特点:
- 元素中键不能重复
- 元素会按照大小顺序排序
2 TreeMap的数据结构
2.1二叉查找树
2.1.1二叉查找树的定义
特点:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有相等的结点;
结论:
二叉查找树就是每个结点的值按照大小排列的二叉树,二叉查找树方便对结点的值进行查找。
图:

2.1.2 二叉查找树的查找操作
查找方式:
从根结点开始,如果要查找的数据等于结点的值, 那就返回。
如果要查找的数据小于结点的值,那就在左子树中递归查找;
如果要查找的数据大于结点的值,那就在右子树中递归查找。
图:

2.2 平衡二叉树
2.2.1平衡二叉树的定义
为了避免出现"瘸子"的现象,减少树的高度,提高我们的搜素效率,又存在一种树的结构:"平衡二叉树"它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。

2.2.2平衡二叉树的旋转
概念:
在构建一棵平衡二叉树的过程中,当有新的结点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构。
两种旋转方式:
左旋:
左旋就是将结点的右支往左拉,右子结点变成父结点,并把晋升之后多余的左子结点出让给降级结点的右子结点;

右旋:
将结点的左支往右拉,左子结点变成了父结点,并把晋升之后多余的右子结点出让给降级结点的左子结点

四种失衡情况:
左左情况,需要以10为基准结点进行右旋

左右情况,先以7为基准结点进行左旋,再以11为基准结点进行右旋

右左情况,先以15为基准结点进行右旋,再以11为基准结点进行左旋

右右情况,以11未基准结点进行左旋

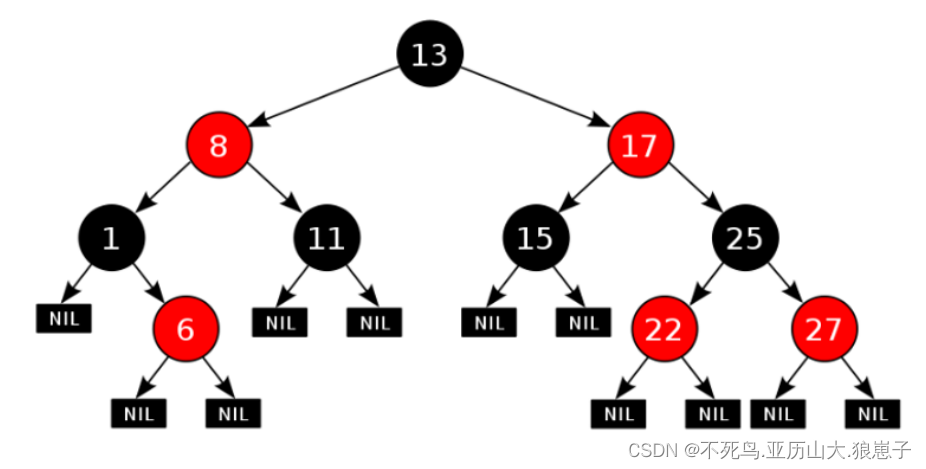
2.3红黑树
2.3.1红黑树的定义
概述:
红黑树是一种自平衡的二叉查找树。
红黑树的每一个结点上都有存储位表示结点的颜色,可以是红或者黑。
红黑树不是高度平衡的,它的平衡是通过"红黑树的特性"进行实现的。
红黑树的特性:
- 每一个结点或是红色的,或者是黑色的;
- 根结点必须是黑色;
- 每个叶结点是黑色的(叶结点是Nil)
- 如果某一个结点是红色,那么它的子结点必须是黑色(不能出现两个红色结点相连的情况)
- 对每一个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点;
图: