因为和焦点弦相关的定理太多,我不会把哪一个公式叫成这样的名字,但百度搜出来就是这个名字
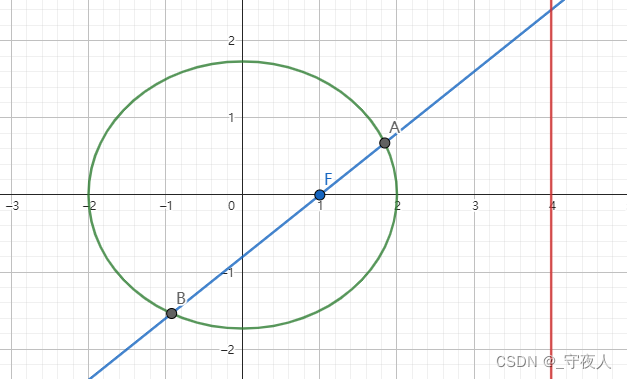
如图,椭圆中焦点弦
A
B
,
∣
F
B
∣
=
k
∣
F
A
∣
(
k
>
0
)
AB, |FB|=k|FA|(k>0)
AB,∣FB∣=k∣FA∣(k>0) ,求
A
B
AB
AB 倾斜角的余弦值
cos
θ
\cos\theta
cosθ。
利用 第二定义
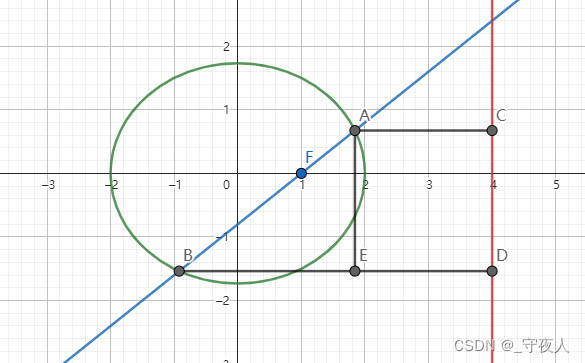
如图,
l
l
l 为椭圆准线,过
A
A
A 做
A
C
⊥
l
AC \perp l
AC⊥l ,过
B
B
B 做
B
D
⊥
l
BD \perp l
BD⊥l ,过
A
A
A 做
A
E
⊥
B
D
AE \perp BD
AE⊥BD
则 A C = ∣ F A ∣ e , B D = k ∣ F A ∣ e , AC=\frac{|FA|}{e},BD=\frac{k|FA|}{e}, AC=e∣FA∣,BD=ek∣FA∣,
B E = ( k − 1 ) ∣ F A ∣ e , A B = ( k + 1 ) ∣ F A ∣ BE=\frac{(k-1)|FA|}{e}, AB=(k+1)|FA| BE=e(k−1)∣FA∣,AB=(k+1)∣FA∣
∴ cos θ = B E A B = k − 1 e ( k + 1 ) , \therefore \cos \theta=\frac{BE}{AB}=\frac{k-1}{e(k+1)}, ∴cosθ=ABBE=e(k+1)k−1,
e cos θ = k − 1 k + 1 . \bf {e \cos \theta = \frac{k-1}{k+1}}. ecosθ=k+1k−1.
代入计算即可。
抛物线,双曲线中结论相同,
其中抛物线中 e = 1 e=1 e=1 ,结论简化为 cos θ = k − 1 k + 1 \cos \theta = \frac{k-1}{k+1} cosθ=k+1k−1。



![[附源码]Python计算机毕业设计Django交通事故档案管理系统](https://img-blog.csdnimg.cn/d369f1b7905846d1a7a2dfaf9ef566e0.png)

![[附源码]JAVA毕业设计家庭理财管理系统(系统+LW)](https://img-blog.csdnimg.cn/b2d7577c2805493aa0a064dfd01c41ad.png)