本文使用ArcMap10.2,以湖北省为例,通过空间插值,制作湖北省1981-2010年20年平均气温空间分布图
树谷资料库资源大全
1 数据准备
可在中国气象数据网下载湖北省1981-2010共20年的各区站累年平均气温数据和各区站经纬度数据。打开为txt格式

在excel表格中对txt数据进行处理,同时将经纬度数据关联到气温表中。(提示:可自行百度excel文本分列向导和VLookup函数使用方法)
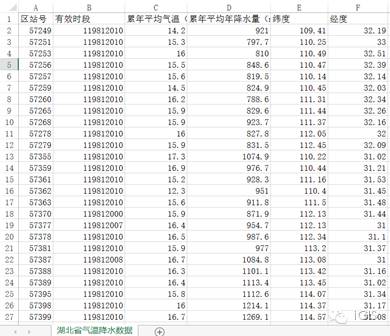
打开ArcMap,添加区站X、Y坐标,坐标系选择WGS84。
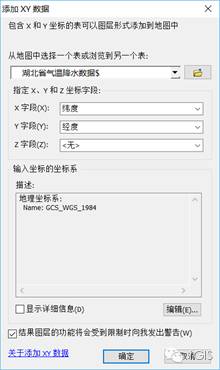
将加载的数据导出成shp文件,如下图所示:

在ArcGIS中,在工具箱依次选择 数据管理工具—投影和转换—要素—投影,将坐标系输出为湖北省级行政区划图矢量文件所采用的坐标系(此处以兰伯特投影为例)
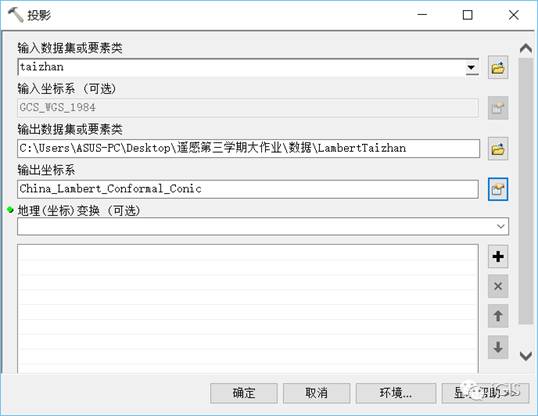
最终同时在ArcMap中加载区站点矢量文件和湖北省级行政区划图矢量文件如下图所示:

2 空间插值
ArcMap中,在工具栏空白处右击打开Geostatistical Analyst工具条,选择地统计向导,统计方法选择克里金法/协同克里金法,数据字段分别选择累年平均气温和海拔高度(插值方法及相应参数设置视具体情况而定,以下仅做参考)

协同克里金法类型选择普通克里金,趋势的移除阶数选择一次

多项式的阶数为1,核函数为指数函数

步长数改为24

扇区类型选择8个扇区
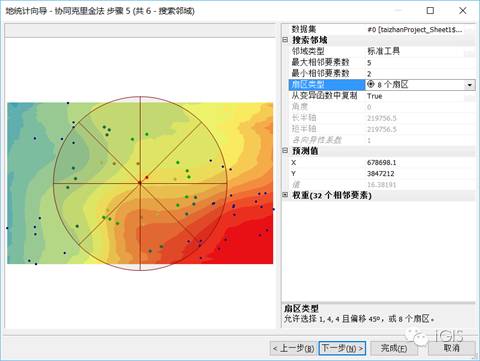
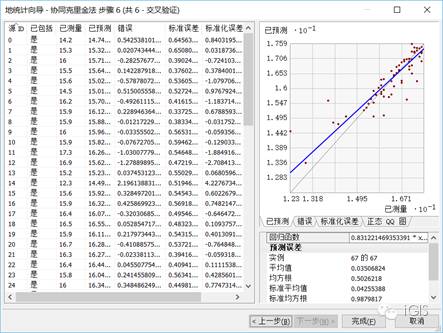
完成后生成的如下图所示
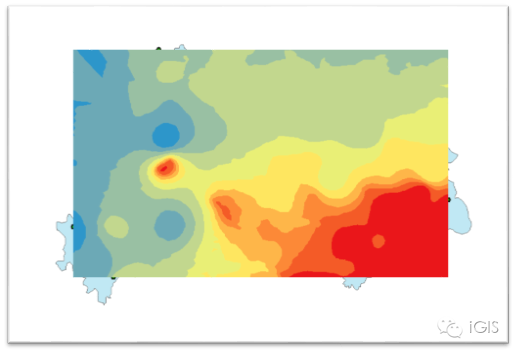
右键选择图层属性,在范围中将范围设置为“矩形范围 省级行政区”
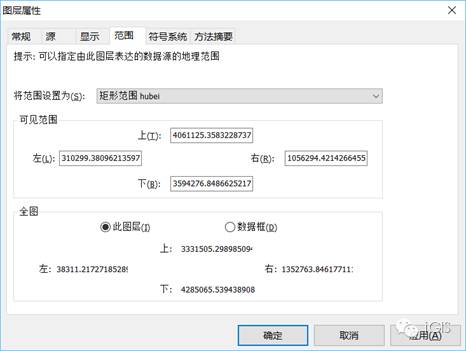
生成的新图层如下所示
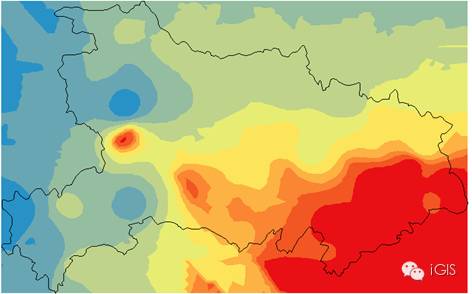
右键图层,依次选择 数据—导出至栅格
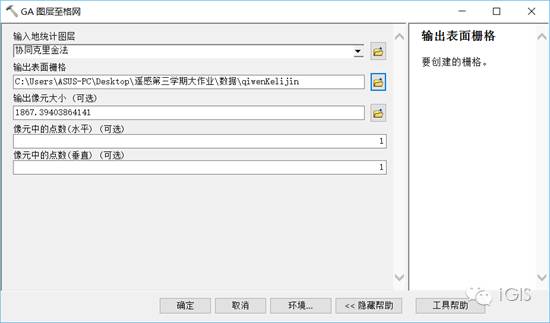
在工具箱中依次选择 Spatial Analyst工具—提取分析—按掩膜提取

掩膜提取后的气温分布图如下
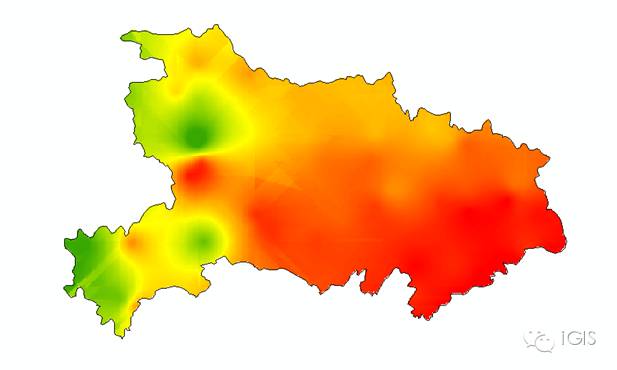
来源:lGIS