以下内容大部分来源于《MATLAB智能算法30个案例分析》,仅为学习交流所用。
1 理论基础
1.1 非线性规划
非线性规划是20世纪50年代形成的一门新兴学科。1951年库恩和塔克发表的关于最优性条件(后来称为库恩·塔克条件)的论文是非线性规划诞生的标志。非线性规划研究一个n元实函数在一组等式或不等式的约束条件下的极值问题,非线性规划的理论来源于1951年库恩·塔克建立的最优条件。20世纪50年代,非线性规划的研究主要注重对梯度法和牛顿法的研究,以Davidon(1959)、Fletcher和Powell(1963)提出的DFP方法为代表。20世纪60年代侧重于对牛顿方法和共轭梯度法的研究,其中以由Broyden、Fletcher、Goldfarb和Shanno从不同角度共同提出的BFGS方法为代表。20世纪70年代是非线性规划飞速发展时期,约束变尺度(SQP)方法(Han和Powell为代表)和Lagrange乘子法(代表人物是Powell和Hestenes)为这一时期的主要研究成果。20世纪80年代以来,随着计算机技术的快速发展,非线性规划方法取得了长足进步,在信赖域法、稀疏拟牛顿法、并行计算、内点法和有限储存法等领域取得了丰硕的研究成果。
1.2 非线性规划函数
函数fmincon是MATLAB最优化工具箱中求解非线性规划问题的函数,它从一个预估值出发,搜索约束条件下非线性多元函数的最小值。函数fmincon的约束条件为:
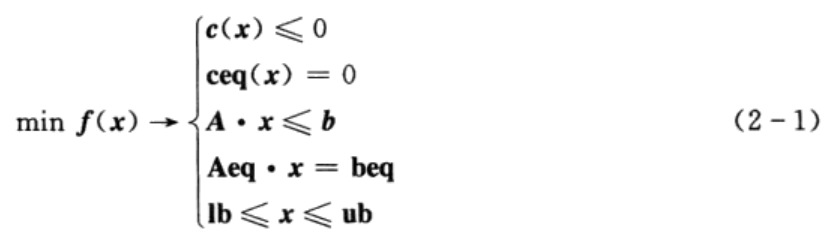
其中,x、b、beq、Ib和ub是矢量;A和Aeq为矩阵;c(x)和ceq(x)返回矢量的函数;f(x)、c (x)和ceq(x)是非线性函数。函数fmincon的基本用法为:
x=fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
其中,lb和ub分别为x的下界和上界。当函数输入参数不包括A、b、Aeq、beq时,默认 A=0、b=0、Aeq=[]、beq=[]。x0为x的初设值。
1.3 遗传算法基本思想
遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法,非常适用于处理传统搜索算法难以解决的复杂和非线性优化问题。目前,遗传算法已被广泛应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域,并在这些领域中取得了良好的成果。与传统搜索算法不同,遗传算法从随机产生的初始解开始搜索,通过一定的选择、交叉、变异操作逐步迭代以产生新的解。群体中的每个个体代表问题的一个解,称为染色体,染色体的好坏用适应度值来衡量,根据适应度的好坏从上一代中选择一定数量的优秀个体,通过交叉、变异形成下一代群体。经过若干代的进化之后,算法收敛于最好的染色体,它即是问题的最优解或次优解。
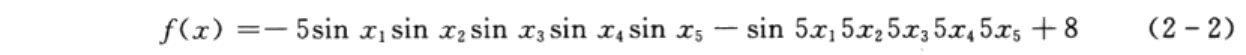

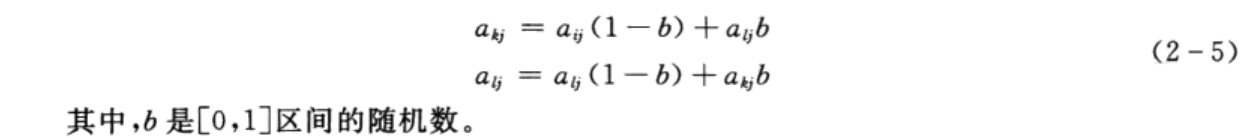

遗传算法提供了求解非线性规划的通用框架,它不依赖于问题的具体领域。遗传算法的优点是将问题参数编码成染色体后进行优化,而不针对参数本身,从而不受函数约束条件的限制;搜索过程从问题解的一个集合开始,而不是单个个体,具有隐含并行搜索特性,可大大减少陷入局部最小的可能性。而且优化计算时算法不依赖于梯度信息,且不要求目标函数连续及可导,使其适于求解传统搜索方法难以解决的大规模、非线性组合优化问题。
经典非线性规划算法大多采用梯度下降的方法求解,局部搜索能力较强,但是全局搜索能力较弱。遗传算法采用选择、交叉和变异算子进行搜索,全局搜索能力较强,但是局部搜索能力较弱,一般只能得到问题的次优解,而不是最优解。因此,本案例结合了两种算法的优点,一方面采用遗传算法进行全局搜索,一方面采用非线性规划算法进行局部搜索,以得到问题的全局最优解。
2 案例背景
2.1 问题描述
采用遗传算法和非线性规划的方法求解如下函数的极小值:
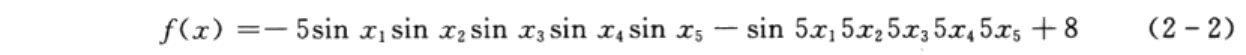
其中,x1、x2、x3、x4、x5是0~0.9π之间的实数。该函数的最小值为-2,最小值位置为(π/2,π/2,π/2,π/2,π/2)。
2.2 算法流程
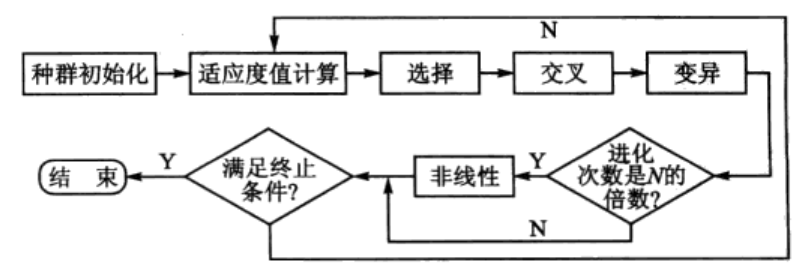
非线性规划遗传算法的算法流程如图1所示。
图1 遗传算法流程图

其中,种群初始化模块根据求解问题初始化种群,适应度值计算模块根据适应度函数计算种群中染色体的适应度值,选择、交叉和变异为遗传算法的搜索算子,N为固定值,当进化次数为N的倍数时,则采用非线性寻优的方法加快进化,非线性寻优利用当前染色体值采用函数fmincon寻找问题的局部最优值。
2.3 遗传算法实现
1.种群初始化
由于遗传算法不能直接处理问题空间的参数,因此必须通过编码把要求问题的可行解表示成遗传空间的染色体或者个体。常用的编码方法有位串编码、Grey编码、实数编码(浮点法编码)、多级参数编码、有序串编码、结构式编码等。实数编码不必进行数值转换,可以直接在解的表现型上进行遗传算法操作。因此本案例采用该方法编码,每个染色体为一个实数向量。
2.适应度函数
适应度函数是用来区分群体中个体好坏的标准,是进行自然选择的唯一依据,一般是由目标函数加以变换得到。本案例是求函数的最小值,把函数值的倒数作为个体的适应度值。函数值越小的个体,适应度值越大,个体越优。适应度计算函数为

3.选择操作
选择操作从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体。个体被选中的概率跟适应度值有关,个体适应度值越高,被选中的概率越大。遗传算法选择操作有轮盘赌法、锦标赛法等多种方法,本案例选择轮盘赌法,即基于适应度比例的选择策略,个体i被选中的概率为
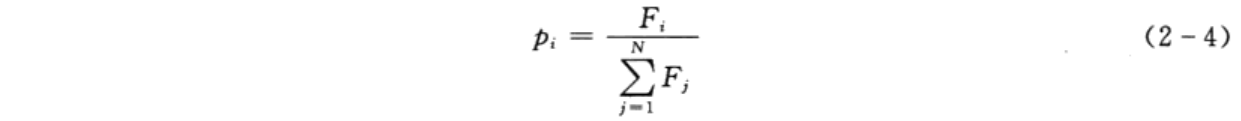
其中,Fi为个体i的适应度值;N为种群个体数目。
4.交叉操作
交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。由于个体采用实数编码,所以交叉操作采用实数交叉法,第k个染色体a;和第l个染色体a:在j位的交叉操作方法为
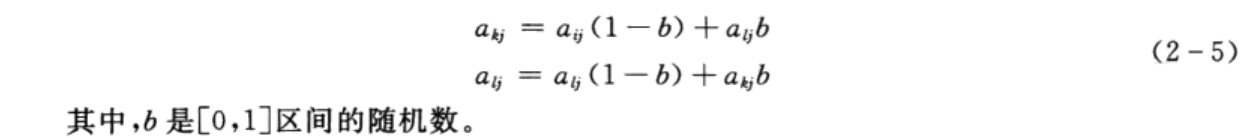
5.变异操作
变异操作的主要目的是维持种群多样性。变异操作从种群中随机选取一个个体,选择个体中的一点进行变异以产生更优秀的个体。第i个个体的第j个基因a,进行变异的操作方法为

6.非线性寻优
遗传算法每进化一定代数后,以所得到的结果为初始值,采用MATLAB优化工具箱中线性规划函数fmincon进行局部寻优,并把寻找到的局部最优值作为新个体染色体继续进化。
3 MATLAB程序实现
根据遗传算法和非线性规划理论,在MATLAB软件中编程实现基于遗传算法和非线性规划的函数寻优算法。
3.1 适应度函数
个体的适应度值为适应度函数值的倒数,适应度函数如下,对其取倒数即为个体适应度值。
function y = fun(x)
y=-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))+8;
3.2 选择操作
选择操作采用轮盘赌法从种群中选择适应度好的个体组成新种群。
function ret=Select(individuals,sizepop)
% 本函数对每一代种群中的染色体进行选择,以进行后面的交叉和变异
% individuals input : 种群信息
% sizepop input : 种群规模
% opts input : 选择方法的选择
% ret output : 经过选择后的种群
individuals.fitness= 1./(individuals.fitness);
sumfitness=sum(individuals.fitness);
sumf=individuals.fitness./sumfitness;
index=[];
for i=1:sizepop %转sizepop次轮盘
pick=rand;
while pick==0
pick=rand;
end
for j=1:sizepop
pick=pick-sumf(j);
if pick<0
index=[index j];
break; %寻找落入的区间,此次转轮盘选中了染色体i,注意:在转sizepop次轮盘的过程中,有可能会重复选择某些染色体
end
end
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;3.3 交叉操作
交叉操作是从种群中选择两个个体,按一定概率交叉得到新个体。
function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss input : 交叉概率
% lenchrom input : 染色体的长度
% chrom input : 染色体群
% sizepop input : 种群规模
% ret output : 交叉后的染色体
for i=1:sizepop
% 随机选择两个染色体进行交叉
pick=rand(1,2);
while prod(pick)==0
pick=rand(1,2);
end
index=ceil(pick.*sizepop);
% 交叉概率决定是否进行交叉
pick=rand;
while pick==0
pick=rand;
end
if pick>pcross
continue;
end
flag=0;
while flag==0
% 随机选择交叉位置
pick=rand;
while pick==0
pick=rand;
end
pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同
pick=rand; %交叉开始
v1=chrom(index(1),pos);
v2=chrom(index(2),pos);
chrom(index(1),pos)=pick*v2+(1-pick)*v1;
chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
flag1=test(lenchrom,bound,chrom(index(1),:)); %检验染色体1的可行性
flag2=test(lenchrom,bound,chrom(index(2),:)); %检验染色体2的可行性
if flag1*flag2==0
flag=0;
else flag=1;
end %如果两个染色体不是都可行,则重新交叉
end
end
ret=chrom;
3.4 变异操作
变异操作是从种群中随机选择一个个体,按一定概率变异得到新个体。
function ret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound)
% 本函数完成变异操作
% pcorss input : 变异概率
% lenchrom input : 染色体长度
% chrom input : 染色体群
% sizepop input : 种群规模
% pop input : 当前种群的进化代数和最大的进化代数信息
% ret output : 变异后的染色体
for i=1:sizepop
% 随机选择一个染色体进行变异
pick=rand;
while pick==0
pick=rand;
end
index=ceil(pick*sizepop);
% 变异概率决定该轮循环是否进行变异
pick=rand;
if pick>pmutation
continue;
end
flag=0;
while flag==0
% 变异位置
pick=rand;
while pick==0
pick=rand;
end
pos=ceil(pick*sum(lenchrom)); %随机选择了染色体变异的位置,即选择了第pos个变量进行变异
v=chrom(i,pos);
v1=v-bound(pos,1);
v2=bound(pos,2)-v;
pick=rand; %变异开始
if pick>0.5
delta=v2*(1-pick^((1-pop(1)/pop(2))^2));
chrom(i,pos)=v+delta;
else
delta=v1*(1-pick^((1-pop(1)/pop(2))^2));
chrom(i,pos)=v-delta;
end %变异结束
flag=test(lenchrom,bound,chrom(i,:)); %检验染色体的可行性
end
end
ret=chrom;3.5 算法主函数
遗传算法主函数流程如下:
(1)随机初始化种群。
(2)计算种群适应度值,从中找出最优个体。
(3)选择操作。
(4)交叉操作。
(5)变异操作。
(6)非线性寻优。
(7)判断进化是否结束,若否,则返回步骤(2)。
主函数MATLAB代码如下:
%% 清空环境
clc
clear
%% 遗传算法参数
maxgen=30; %进化代数
sizepop=100; %种群规模
pcross=[0.6]; %交叉概率
pmutation=[0.01]; %变异概率
lenchrom=[1 1 1 1 1]; %变量字串长度
bound=[0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi]; %变量范围
%% 个体初始化
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %种群结构体
avgfitness=[]; %种群平均适应度
bestfitness=[]; %种群最佳适应度
bestchrom=[]; %适应度最好染色体
% 初始化种群
for i=1:sizepop
individuals.chrom(i,:)=Code(lenchrom,bound); %随机产生个体
x=individuals.chrom(i,:);
individuals.fitness(i)=fun(x); %个体适应度
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[];
%% 进化开始
for i=1:maxgen
% 选择操作
individuals=Select(individuals,sizepop);
avgfitness=sum(individuals.fitness)/sizepop;
% 交叉操作
individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
% 变异操作
individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);
% 计算适应度
for j=1:sizepop
x=individuals.chrom(j,:);
individuals.fitness(j)=fun(x);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(individuals.fitness);
[worestfitness,worestindex]=max(individuals.fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=individuals.chrom(newbestindex,:);
end
individuals.chrom(worestindex,:)=bestchrom;
individuals.fitness(worestindex)=bestfitness;
avgfitness=sum(individuals.fitness)/sizepop;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束
%% 结果显示
[r c]=size(trace);
figure
plot([1:r]',trace(:,1),'r-',[1:r]',trace(:,2),'b--');
title(['函数值曲线 ' '终止代数=' num2str(maxgen)],'fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('函数值','fontsize',12);
legend('各代平均值','各代最佳值');
disp('函数值 变量');
ylim([1.5 8])
%xlim([1,size(trace,1)])
grid on
% 窗口显示
disp([bestfitness x]);
3.6 非线性寻优
调用MATLAB最优化工具箱中函数fmincon进行非线性寻优:
function ret = nonlinear(chrom,sizepop)
for i=1:sizepop
x=fmincon(inline('-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))'),chrom(i,:)',[],[],[],[],[0 0 0 0 0],[2.8274 2.8274 2.8274 2.8274 2.8274]);
ret(i,:)=x';
end3.7 结果分析
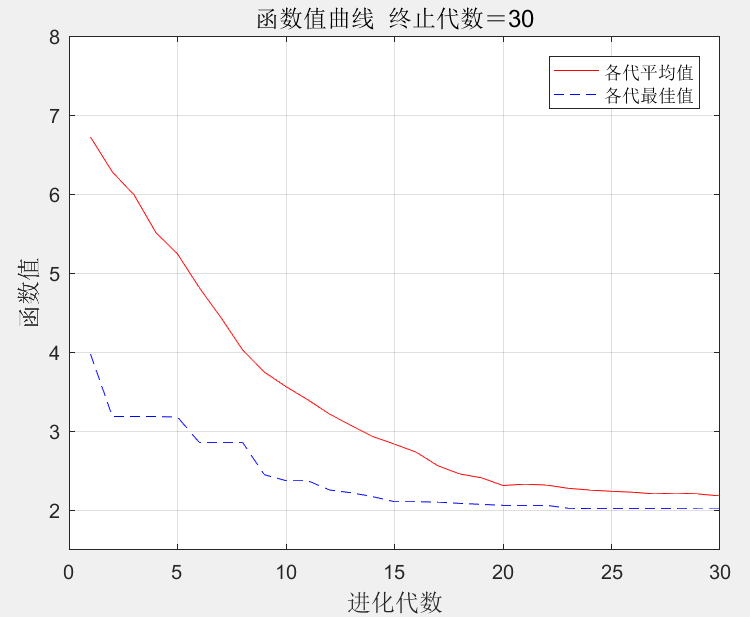
根据遗传算法理论,在MATLAB软件中编程实现基本遗传算法寻找该函数最优解。遗传算法参数设置为:种群规模100,进化次数30,交叉概率为0.6,变异概率为0.1。基本遗传算法优化过程中各代平均函数值和最优个体函数值变化如图2所示。当种群进化到30代时,函数值收敛到2.0193,在x1、x2、x3、x4、x5分别取1.5550、1.6237、1.5736 、1.5863 、1.6230时达到该值。
图2 基本遗传算法收敛曲线

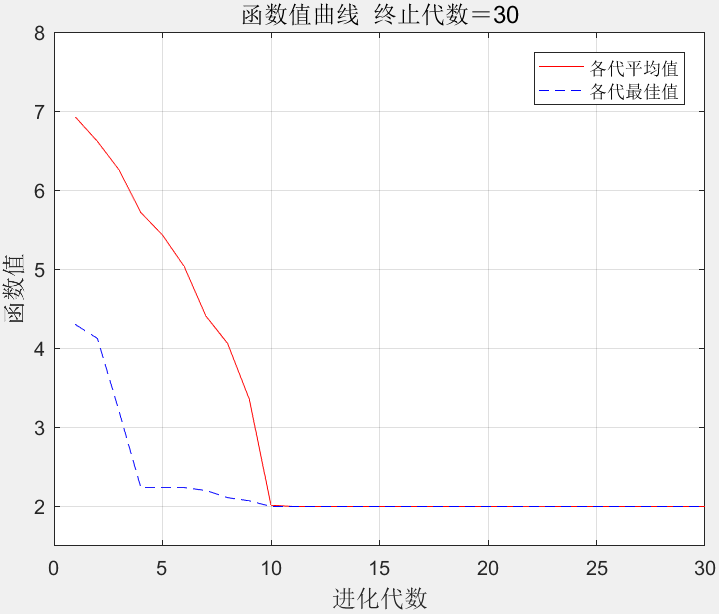
在MATLAB软件中编程实现基于遗传算法和非线性规划的函数寻优算法求解该问题。遗传算法参数设置同前,即种群规模100,进化次数30次,交叉概率0.6,变异概率0.1。算法优化过程中各代平均函数值和最优个体函数值变化如图3所示。当种群进化到30代时,函数值收敛到2.0000,在x1、x2、x2、x3、x4分别取1.5708、1.5708、1.5708、1.5708、1.5708时达到该值。
图3
遗传算法和非线性规划结合的收敛曲线

比较图2与图3可见,在同等条件下,基于遗传算法和非线性规划的函数寻优算法在收敛速度和求解结果上优于基本的遗传算法。可见,将非线性规划方法同遗传算法相结合,提高了遗传算法的搜索性能。
4完整代码
完整matlab代码可以从以下链接获取:
基于遗传算法和非线性规划的函数寻优算法