6-4布线问题（分支限界）

一、问题描述

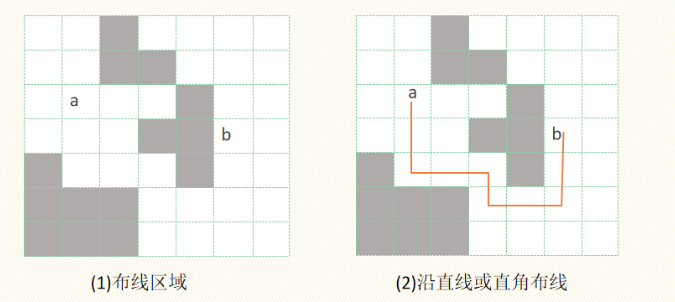
印刷电路板将布线区域划分成m*n个方格阵列,如图(1)所示。
精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案。
在布线时,电路只能沿直线或直角布线,如图(2)所示。
为了避免线路相交，已布了线的方格做了封锁标记,其他线路不允许穿过被封锁的方格。

二、分析

算法的思想: 队列式分治限界法
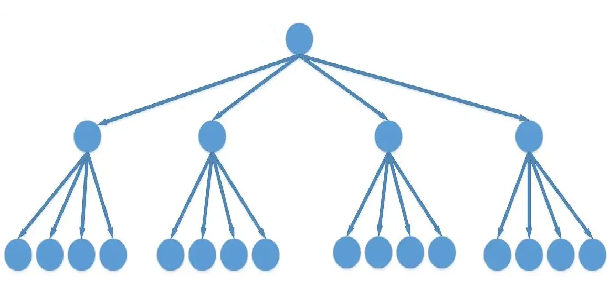
每个点的下一步有四个可选位置（上下左右)

解空间树是4叉树

位置偏移量：
int go[4][2]={{-1,0},{1,0},{0,-1},{0,1}}; //上下左右

int m,n;//m行n列;
int grid[100][100];
struct node{
int x;
int y;
};
node start,end;//从start到end
//初始化

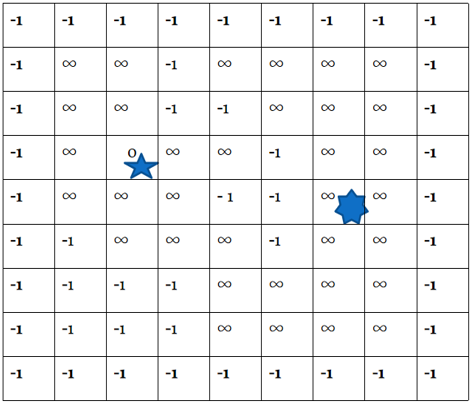
void Init(){//初始化 
	for(int i=0;i<=m+1;i++){
		for(int j=0;j<=n+1;j++){
			if(i==0||j==0||i==m+1||j==n+1)
				grid[i][j]=-1;//四周初始化为-1    
			else grid[i][j]=INF; //其余初始化为无穷大
		}
	} 
}

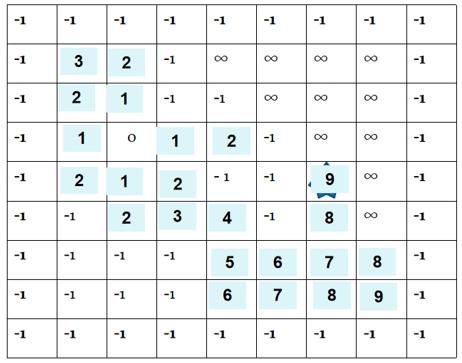
//广搜+剪枝
剪枝策略：新扩展的该位置路径长度小于该位置已记录的值

bool IsEnd(node t){//判断到没到终点 
	if(t.x==end.x&& t.y==end.y) //到终点了 
		return true;
	else return false;
}
bool FindPath(){//广搜 
	if(IsEnd(start)) return true;//判断起点是不是等于终点
	queue<node>q;
	int newx,newy; node no;
	q.push(start);//起点入队 
	while(!q.empty() ){
		no=q.front(); q.pop();//取出队首 
		for(int i=0;i<4;i++) { //四个方向上下左右 
			newx=no.x+go[i][0];
			newy=no.y+go[i][1];
			if(grid[no.x][no.y]+1 < grid[newx][newy]){//剪枝 
				grid[newx][newy] = grid[no.x][no.y]+1;
				node t;
				t.x = newx;
				t.y = newy;
				if(IsEnd(t)) return true;//到终点了						
				else q.push(t);	//否则入队			
			}		
		}
	}
	return false; 
}

构造最优解

void BestL(int x,int y){//构造最优解 
	int newx,newy;
	for(int i=3;i>=0;i--) {
		newx=x+go[i][0];
		newy=y+go[i][1];
		if(grid[x][y]==grid[newx][newy]+1){
			BestL(newx,newy);
			cout<<"("<<newx<<","<<newy<<") -> ";
			break;
		}
	}
	return;	
} 

三、完整代码

//6-4布线问题 
//队列式分支限界 4叉树  
#include<iostream>
#include<queue>
#define INF 0x3f3f
using namespace std;
int m,n;//m行n列; 
int grid[100][100];
int go[5][3]={{-1,0},{1,0},{0,-1},{0,1}};//上下左右 
struct node{
	int x;
	int y;
};
node start,end;//从start到end 
void Init(){//初始化 
	for(int i=0;i<=m+1;i++){
		for(int j=0;j<=n+1;j++){
			if(i==0||j==0||i==m+1||j==n+1)
				grid[i][j]=-1;//四周初始化为-1    
			else grid[i][j]=INF; //其余初始化为无穷大
		}
	} 
}
void Print(){
	for(int i=0;i<=m+1;i++){
		for(int j=0;j<=n+1;j++){
			printf("%5d  ",grid[i][j]);
		}
		cout<<endl;
	} 
}
bool IsEnd(node t){//判断到没到终点 
	if(t.x==end.x&& t.y==end.y) //到终点了 
		return true;
	else return false;
}
bool FindPath(){//广搜 
	if(IsEnd(start)) return true;//判断起点是不是等于终点
	queue<node>q;
	int newx,newy; node no;
	q.push(start);//起点入队 
	while(!q.empty() ){
		no=q.front(); q.pop();//取出队首 
		for(int i=0;i<4;i++) { //四个方向上下左右 
			newx=no.x+go[i][0];
			newy=no.y+go[i][1];
			if(grid[no.x][no.y]+1 < grid[newx][newy]){//剪枝 
				grid[newx][newy] = grid[no.x][no.y]+1;
				node t;
				t.x = newx;
				t.y = newy;
				if(IsEnd(t)) return true;//到终点了						
				else q.push(t);	//否则入队			
			}		
		}
	}
	return false; 
}
void BestL(int x,int y){//构造最优解 
	int newx,newy;
	for(int i=3;i>=0;i--) {
		newx=x+go[i][0];
		newy=y+go[i][1];
		if(grid[x][y]==grid[newx][newy]+1){
			BestL(newx,newy);
			cout<<"("<<newx<<","<<newy<<") -> ";
			break;
		}
	}
	return;	
} 
int main(){
	int t;//障碍物的个数 
	int x,y;
	cin>>m>>n;
	Init();//初始化为无穷大，四周初始化为-1 
	cin>>start.x>>start.y>>end.x>>end.y;//输入起点和终点 
	cin>>t;
	while(t--){
		cin>>x>>y;
		grid[x][y]=-1;
	}
	grid[start.x][start.y]=0;
	if(FindPath()){
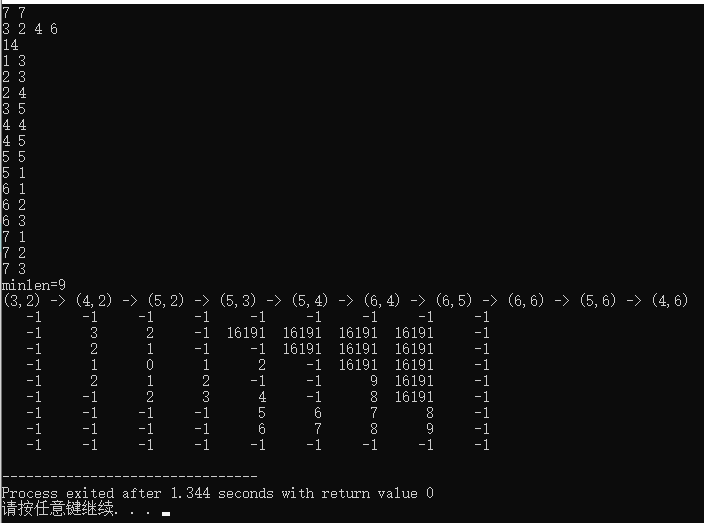
		cout<<"minlen="<<grid[end.x][end.y]<<endl;
		BestL(end.x,end.y);
		cout<<"("<<end.x<<","<<end.y<<")\n";
	} 
	else{
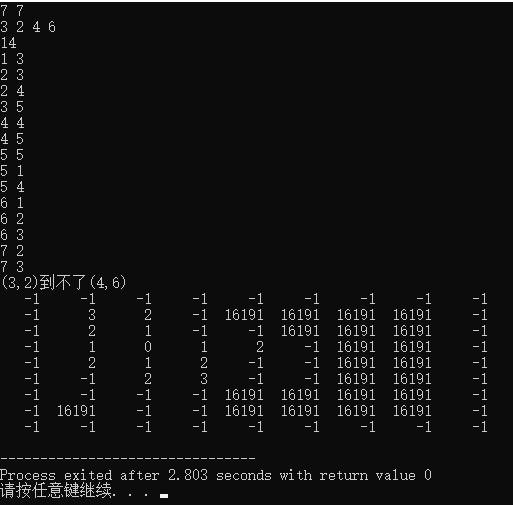
		cout<<"("<<start.x<<","<<start.y<<")到不了("<<end.x<<","<<end.y<<")\n";
	}
	Print();
	return 0;
}
/*有路
7 7
3 2 4 6
14
1 3
2 3
2 4
3 5
4 4
4 5
5 5
5 1
6 1
6 2
6 3
7 1
7 2
7 3
*/
/*
没有路的情况 
7 7
3 2 4 6
14
1 3
2 3
2 4
3 5
4 4
4 5
5 5
5 1
5 4
6 1
6 2
6 3
7 2
7 3
*/

有最短路

没有最短路