目录

堆的概念

堆的实现

堆的存储结构

堆的插入操作

堆的删除操作

堆的创建

向上调整建堆和向下调整建堆

堆排序

堆的应用 - topK问题

---

堆的概念

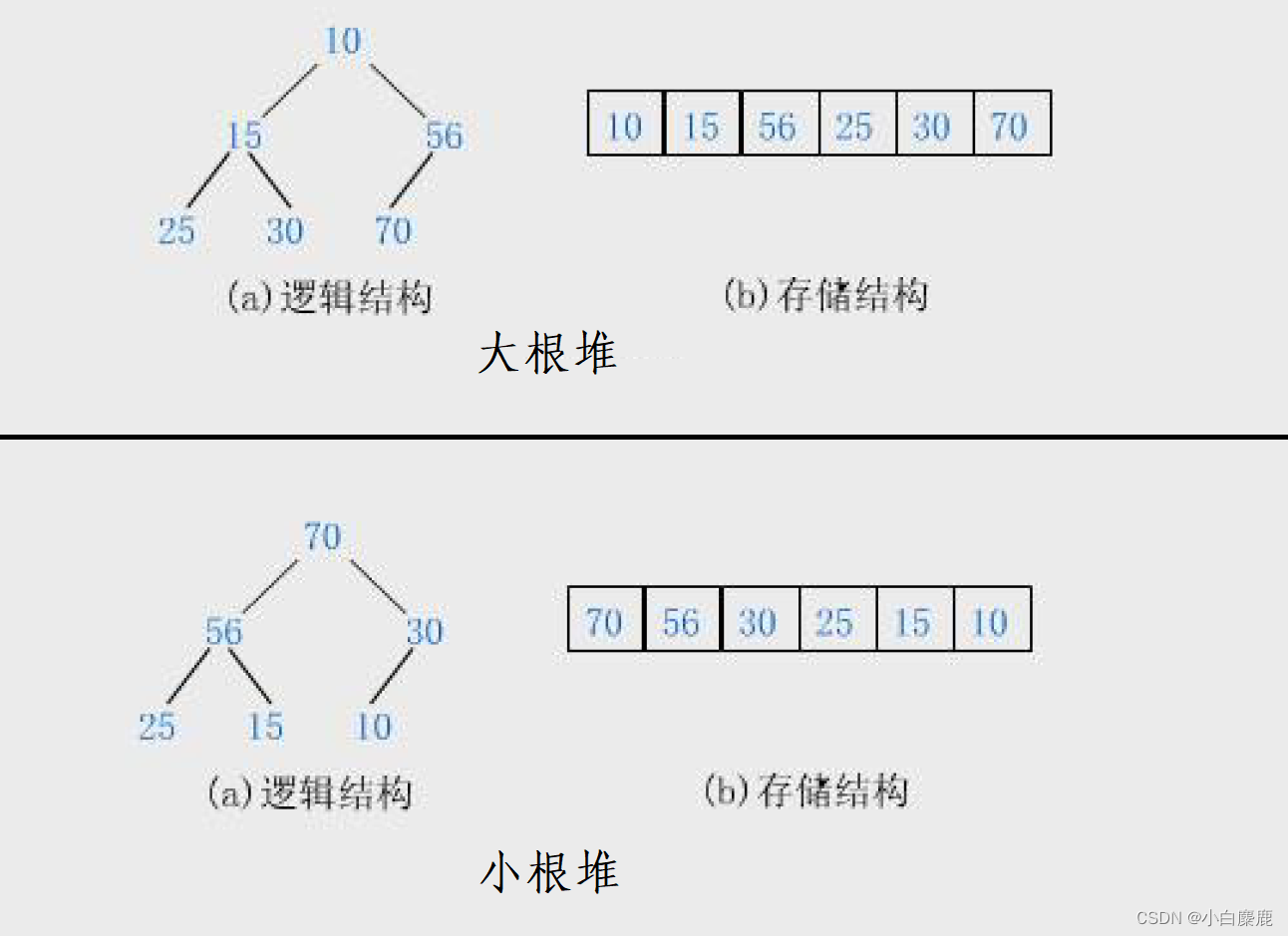
“堆”是计算机科学中一种数据结构，可以看作是一棵完全二叉树。通常满足堆的性质：父节点的值总是大于或等于其子节点的值，这种堆称为“大根堆”（或父节点的值总是小于或等于其子节点的值，这种堆称为“小根堆”）。堆常用于实现优先队列等数据结构，也被广泛应用于操作系统中的内存分配等领域。

简言之就是，可以把堆理解为一种特殊的完全二叉树。是一种类似金字塔的结构，如果是“小根堆”，那么对于任意父节点，其父节点的值一定小于其左右孩子；如果是“大根堆”，那么对于任意父节点，其父节点的值一定大于其左右孩子。需要注意的是，堆一般是父节点与孩子节点之间的联系，而左右孩子之间并没有直接的大小关系。可以参考下面的图示来理解。

堆的实现

堆的存储结构

由于堆是一种完全二叉树，所以我们可以用数组来存储堆的节点信息。所以一般可以把数组理解为一颗完全二叉树，但并不一定是堆，需要满足其性质才是堆。

需要注意的是，如果下标从0开始，那么对于任意节点下标n，其孩子节点的下标为2*n+1(左)、2*n+2(右)，其父节点的下标为(n-1)/2。如果下标从1开始，那么对于任意节点下标n，其孩子节点的下标为2*n(左)、2*n+1(右)，其父节点的下标为n/2。所以根节点的起始下标不同，查找父母(孩子)节点对应的计算方式也是不同的，不要思维定势了。

堆的插入操作

由于堆是一种具有特定排序规则的二叉树，修改操作的维护成本过高，所以一般不讨论堆这种数据结构的修改操作。又由于堆是用数组实现的，所以查找操作非常简单，这里也就不再说了(就相当于对数组查找)。所以我们这里只讲解堆的插入和删除操作。 

以小根堆为例，堆的插入操作的大体思路是：先将待插入的数据尾插到堆中，然后再对这个堆进行向上调整。

向上调整的过程是：将这个新插入的数据不断和其父节点比较，如果其比父节点小就将其与父节点的数据交换。然后其与父节点各向上走一层，如果还是比父节点小就继续交换。然后循环往复，直至其不再比父节点小或者其走到根节点的位置就停止。代码示例如下：

//向上调整。ph是堆的指针，index是新插入节点的下标
void upAdjust(Heap* ph, HPDataType index)
{
	/*从下向上根据条件选择交换调整还是结束循环*/
	assert(ph != NULL);
	HPDataType child = index;
	HPDataType parent = (child - 1) / 2;
	while (child > 0 && ph->_a[child] - ph->_a[parent] < 0)
	{
		intSwap(ph->_a + child, ph->_a + parent);
		child = parent;
		parent = (child - 1) / 2;
	}
}

可见，向上调整顾名思义，就是将下面的节点通过不断向上方调整，进而调整成堆的结构。所以插入操作的代码就很好写了：

//堆的插入
void HeapPush(Heap* ph, HPDataType x)
{
	/*先在最后插入，然后向上调整*/
	assert(ph != NULL);
	capacityCheak(ph);
	ph->_a[ph->_size++] = x;
	upAdjust(ph, ph->_size - 1);
}

• 这里还需要补充一下：

由于向上调整的过程中最多是从最低端走到最上端，所以最坏的情况下需要走O(logN)次（N是节点个数），所以单次向上调整的时间复杂度为O(logN)。由于数组的尾插是常数时间的，所以对应的， 插入操作的时间复杂度也为O(logN)。

需注意，实现这个插入操作（利用向上调整）的一个前提是原本的结构就是一个堆。

堆的删除操作

堆的删除操作就需要用到向下调整了。大体思路为：将数组首尾两个位置的元素交换，然后令堆的size值减一，相当于“屏蔽”了尾的位置。然后对齐进行向下调整。

向下调整的过程如下：从根节点开始，将其与两个孩子节点中较小的一个值进行比对（小根堆），如果其大于这个较小的值，就将它们交换。然后循环往复，直至不再满足这个条件或者走到最后。代码示例如下：

//向下调整
 /*注意，n是数组内元素个数，不是数组最大下标*/
void downAdjust(Heap* ph, HPDataType n, HPDataType parent) //parent是开始位置的下标
{
	/*从上向下不断与左右子树的较小值调整（小根堆的情况）*/
	HPDataType left_child = parent * 2 + 1;
	while (left_child < n)
	{
		HPDataType minChild = left_child;
		if (left_child + 1 < n) //有右子树的情况
			minChild = minNode(ph, left_child, left_child + 1);
		if (ph->_a[parent] > ph->_a[minChild])
			intSwap(ph->_a + parent, ph->_a + minChild);
		parent = minChild;
		left_child = parent * 2 + 1;
	}
}

所以删除操作的代码就可以写了：

//堆的删除
void HeapPop(Heap* ph)
{
	HPDataType tail = --ph->_size;
	intSwap(ph->_a, ph->_a + tail); //此时堆内元素数量刚好为原堆最后一个数的下标
	downAdjust(ph, ph->_size, 0);
}

• 需要补充的是：

向下调整和向上调整一样，最差情况的时间复杂度也为O(logN)。所以删除操作的时间复杂度也是O(logN)的。

向下调整的一个前提也是要保证其下面的节点是堆。

堆的创建

向上调整建堆和向下调整建堆

通过上面的描述我们了解了何为向上调整和向下调整，所以我们就可以利用其建堆了。

向上调整建堆就是从上面开始，不断向下走，边遍历边调整。因为向上调整建堆要保证上面的是堆，所以要从上面开始，直至走到最后一个节点。所以可见这种向上调整建堆的时间复杂度就是显而易见的O(N*logN)（N是节点数）。

向下调整建堆是从下面开始，但不是从最后一个节点开始，而是从第一个非叶子节点开始（因为叶子节点已经没有向下调整的必要了）。而对于一颗有N个节点的完全二叉树，有(N+1)/2个叶子节点，所以就相当于只需要对一半的节点进行向下调整的操作。所以要注意向下调整建堆的时间复杂度并不是O(N*logN)的，而是O(N)的，具体的推导过程如下：

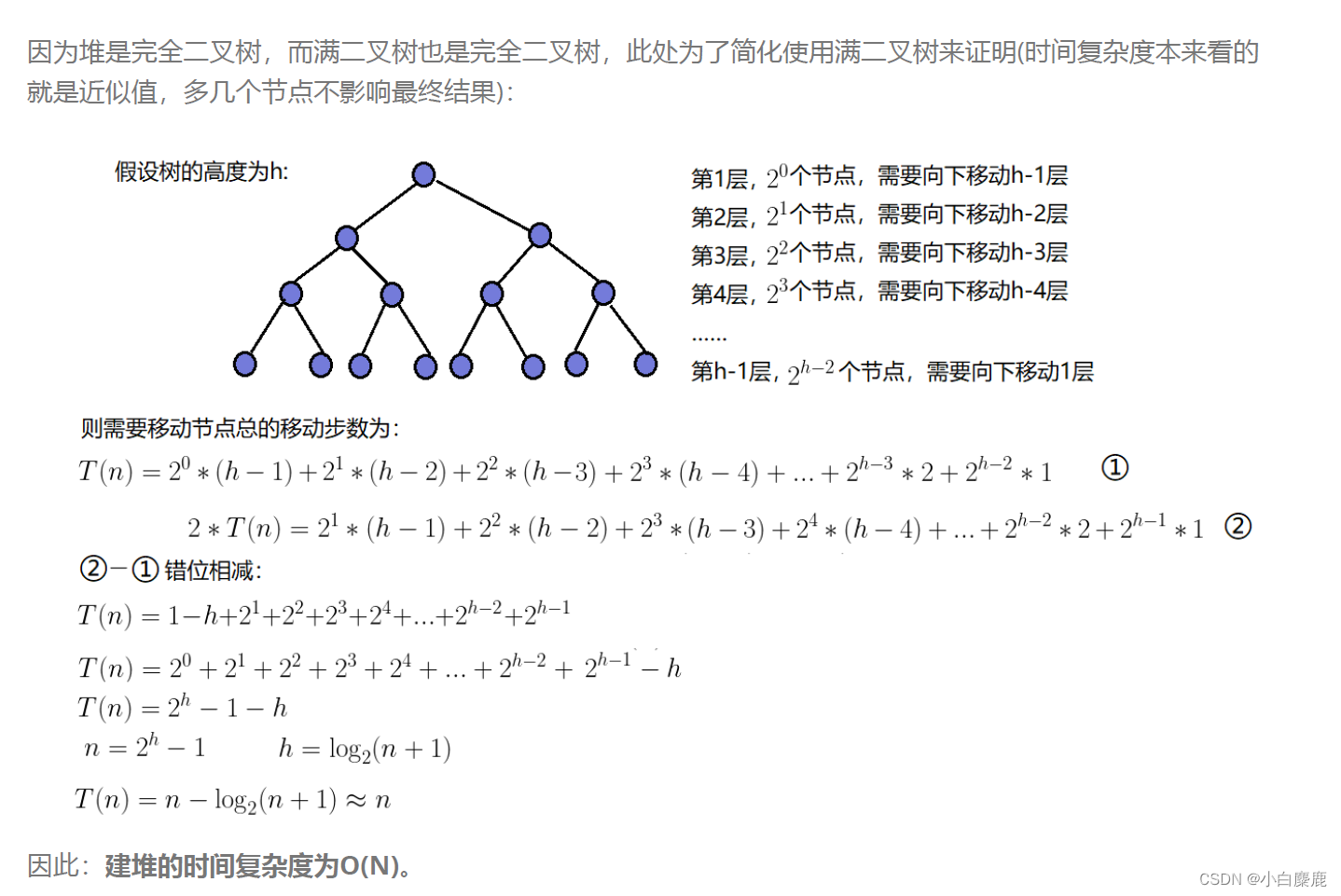
 代码写法如下：

// 堆的构建
void HeapCreate(Heap* ph, HPDataType* a, int n)
{
	assert(ph != NULL);
	assert(a != NULL);
	HeapInit(ph);
	//先把a数组的内容拷贝过来
	memcpy(ph->_a, a, sizeof(a[0]) * n);
	/*
	//法1：向上调整建堆（核心思想：要保证上方是堆）
	for (int i = 1; i < n; i++)
	{
		upAdjust(ph, i);
	}*/
	//法2：向下调整键堆（核心思想：要保证下方是堆）
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		downAdjust(ph, n, i);
	}
}

 上面这种写法好理解，但是显得很呆，所以一般都是用下面这种写法建堆：（由于向下调整建堆明显优于向上调整建堆，所以这里选用向下调整建堆）

//数组（堆）的向下调整（大根堆）
void arrDownAdjust(int* a, int n, int parent) //n是数组内元素个数，不是数组最大下标
{
	/*从上向下不断与左右子树的较小值调整（小根堆的情况）*/
	int left_child = parent * 2 + 1;
	while (left_child < n)
	{
		int maxChild = left_child;
		if (left_child + 1 < n && a[left_child] < a[left_child + 1])
			maxChild = left_child + 1;
		if (a[parent] < a[maxChild])
			intSwap(a + parent, a + maxChild);
		parent = maxChild;
		left_child = parent * 2 + 1;
	}
}

• 总结一下：

常用建堆的方法有两种，向上调整建堆和向下调整建堆。

建堆的核心：向上调整建堆，保证上方是堆；向下调整建堆，保证下方是堆

堆排序

堆排序顾名思义就是利用堆进行的排序。比如我们要对一个数组进行排序，首先可以对其建堆，然后再搞一个数组，不断将堆顶元素尾插到新的数组中，插入之后删除堆顶元素（删除操作是有堆的自调整的）。此时堆排序就完成了。

但这种方法太呆了，我们可以直接在原数组中排序。即我们每次将堆顶与数组中最后一个元素互换位置，然后调整堆（相当于一次删除/pop操作）。这样我们最后得到的就是一个有序的数组了。但要注意的是，如果想要得到一个升序数组，要建立的并不是小根堆，而是大根堆。因为如果是小根堆，相当于每次把一个当前最小的数放到后面，所以这样最后的出来的结果就是小的在后大的在前。而大根堆则相反，得出来的刚好是升序的。这里就相当于将原来半有序的堆，”反转“一下让其变得有序。所以升序要用大根堆，降序要用小根堆。具体代码如下：

// 对数组进行堆排序（堆排序）
void HeapSort(int* a, int n)
{
	/*数组升序排列：建大根堆，然后“反转”大根堆*/
	assert(a != NULL);
	//向下调整键堆
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		arrDownAdjust(a, n, i);
	}
	//“反转”大根堆
	for (int i = 0; i < n - 1; i++) //只需要循环n-1次就可以了
	{
		arrPop(a, n - i);
	}
}

• 补充一点：

堆排序的时间复杂度为O(N*logN)，其中N为节点数。

堆的应用 - topK问题

topK问题就是在一个乱序数组中找到前K个大/小的数。对于这类问题很容易想到可以用堆，将数组建堆，然后执行k次top操作和pop操作就可以得到前k个大/小的数了。这种做法的时间复杂度为O(NlogN)。这么做对于处理大量数据的情况就显得很冗杂。

例如要找到1000000个数中的前7个大数，直接建一个1000000大小的堆就显得有些大材小用了。所以我们可以建一个大小为7的小根堆，然后不断将这1000000个数进行选择入堆，如果其大于堆顶的元素，就将其与堆顶元素置换，然后调整堆。这样最终得到的堆就是我们要的前7个大的数，其中堆顶的元素是这7个数中最小的那个。这种做法的时间复杂度就被缩短1为O(N)了

这里之所以设小堆是因为如果设大堆，那么就会导致有可能只会筛选出最大的那个数，其它的k-1个数都被这个最大的数给”挡“在外面了。具体的代码写法如下：

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<limits.h>

/*这些函数写在上面显得冗杂，所以就写在下面，只在这里声明一下*/
void HeapCreate(int* a, int n); 
void DownAdjust(int* a, int n, int parent);
//topK
void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000; 
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void PrintTopK(int k)
{
	//打开文件
	const char* file = "data.txt";
	FILE* fin = fopen(file, "r");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}
	//找topK
	int* a = (int*)calloc(k, sizeof(int));
	for (int i = 0; i < k; i++ )
	{
		fscanf(fin, "%d", a + i);
	}
	HeapCreate(a, k);

	while (!feof(fin))
	{
		int cur;
		fscanf(fin, "%d", &cur);
		if (cur > a[0])
		{
			a[0] = cur;
			DownAdjust(a, k, 0);
		}
	}	
	for (int i = 0; i < k; i++)
	{
		printf("%d   ", a[i]);
	}
	//销毁动态数组，关闭文件
	free(a);
	fclose(fin);
}

int main()
{
	//CreateNDate(); //造完数据之后把它注释掉，这样好观察
	PrintTopK(7);

}