学习二叉树之前我们首先要对树有一个认识，树是一种非线性结构，它是由n(n>=0)个有限节点组成的一个具有层次关系的节点；而这个层次结构倒过来看就十分的像一棵树，所以起名树结构。

跟现实中的树一样，树结构也有一个根，这个根节点是没有先驱节点的，可以认为其是始源

除根结点外，其余结点被分成M(M>0)个互不相交的集合，其中每一个集合又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继；从这段定义中我们就可以看到其有递归的影子，一个节点即是一个子节点也是一个根节点

下面我们对几个定义进行学习

        1、树是非线性结构

        2、任何一颗树都由根和子树够成

        3、节点的度：指拥有几个子树

        4、叶子节点就是度为0的树

        5、兄弟节点：具有相同父亲节点的节点

        6、树的深度和高度：树中节点的最大层次

        7、森林：指多棵树互不相交的集合

        8、节点的祖先：从根节点到该节点所经分支的所有节点；子孙：以某节点为根的子树中任一节点都成为该节点的子孙

       注意：在树结构中子树是不相交的

                  除根节点每一个节点都只有一个父节点

                  一个N个节点的树有N-1条边

那么下面我们就来学习如何定义一个树形结构，先看看树形结构长什么样()

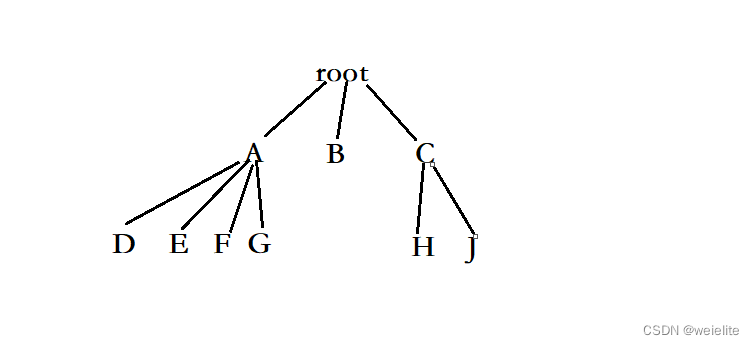那么看到这就有小伙伴问了，这些个节点怎么连起来的啊，他们的值又是怎么保存的

那么请看代码

typedef int Node_Date
typedef struct Node
{
    struct Node*left_child;    //用于指向左子节点
    struct Node*right_child;   //用于指向右子节点
    Node_Date x;               //用于存放数据，数据的类型更改则需要更改typedef
}Node;

了解：当然还有一种表示方法：即左孩子又兄弟结构

        在我们不知道度是多少的时候左孩子右兄弟表示法会方便很多：只找到第一个孩子，剩下的让兄弟指针依次相连具体什么样让我们看一张图

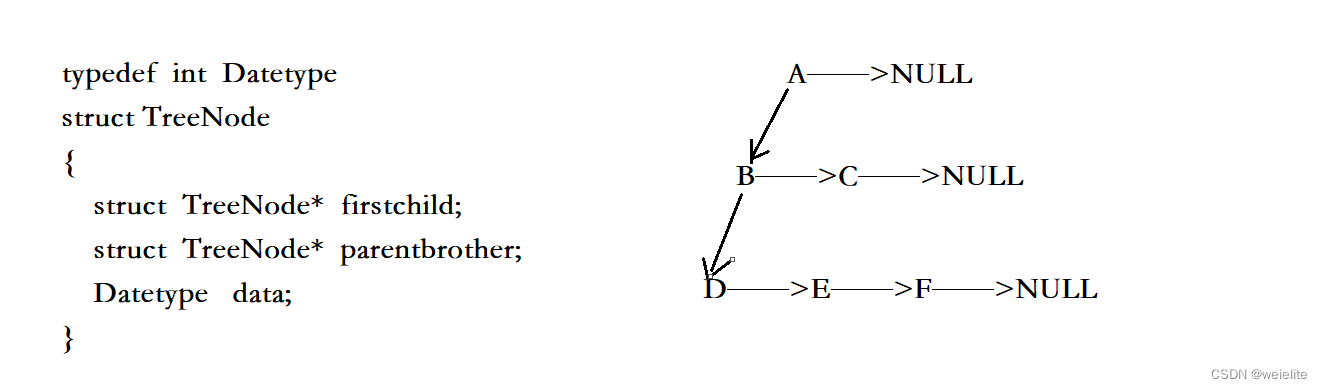
在了解完树形结构后，我们来学习树中很重要的一种二叉树，顾名思义就是每一个节点最大的度为2即最多有两个子节点；上图

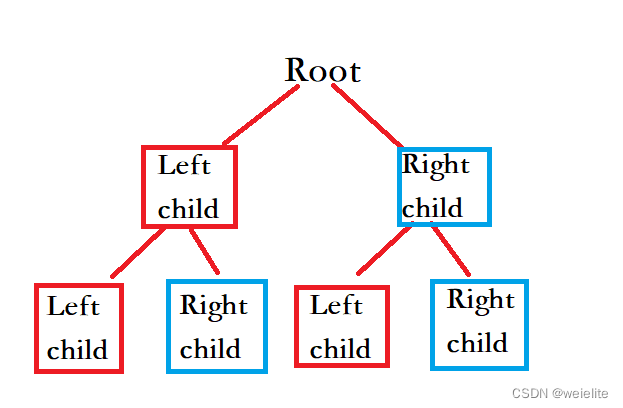
二叉树特性：1、二叉树不存在度大于2的节点

                      2、二叉树有左右子树之分，次序不能颠倒；因此二叉树是有序树

二叉树存在以下几种情况

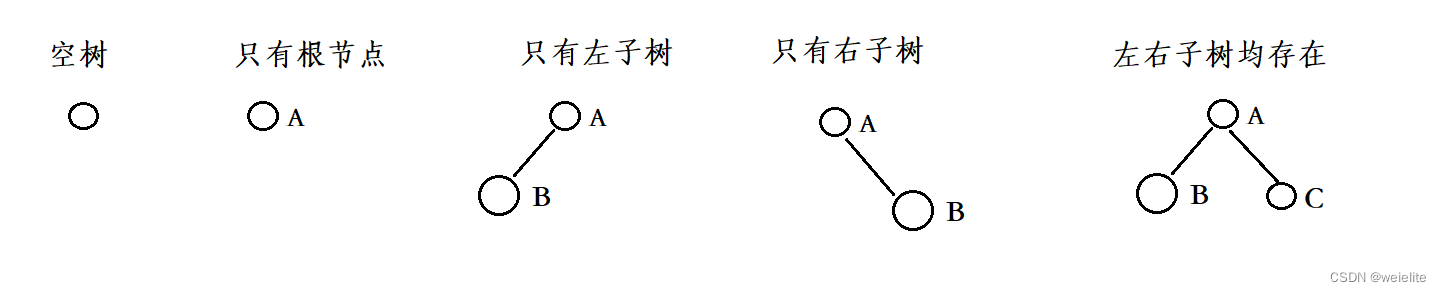
 二叉树分为：满二叉树与完全二叉树

       满二叉树：每一层都是满的(高度为h)

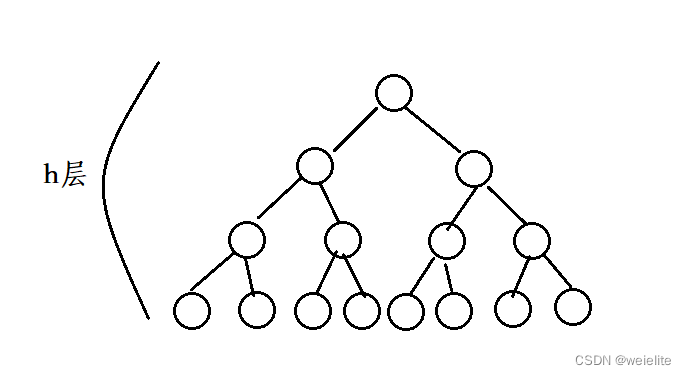
 计算节点个数：S=2^0+2^1+2^2+.......+2^(n-1) =2^h  -1

满二叉树有n个节点，则高度h为log 2^(n+1)

        完全二叉树：前h-1层都是满的(高度为h)，且最后一层是从左向右依次连续

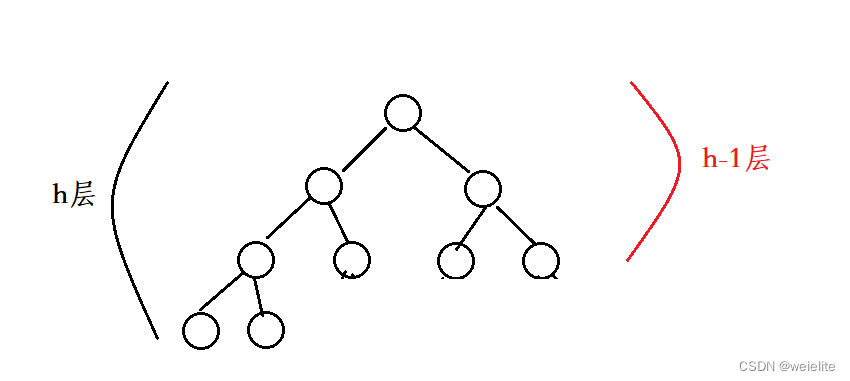
 节点个数：2^(h-1)-1+1   ~    2^h -1;

计算完全二叉树我们可以理解为h-1层是满的再加1个，也可以理解为差1个节点第h层就满了，相当于2^h-1个这两种情况之内都是第h层的范畴内

完全二叉树有N个节点则高度h为 log2^N+1  ~   log2^(N+1)

结论：对于任何一颗二叉树，如果度为0其叶节点个数为n0

           度为2的分支节点个数为n2，则有n0=n2+1

           即度为0的个数比度为2的多一个

例1：具有2n个节点的完全二叉树种叶子节点个数为多少？

        2n=n0+n1+n2  =n0+n1+n0-1    =2*n0-1+n1  =n1-1;

因为

1、度为0的比度为2的多一个，此处n0为叶子节点，n1为一个叶子节点，n2为两个叶子节点

2、完全二叉树度为1的节点要么为1要么为0

综上两条度为1的叶子节点只能是1；

在对二叉树的基本概念与定义有所学习后，我们来看看二叉树的遍历

二叉树遍历：前序遍历、中序遍历、后序遍历、层序遍历

前序：根节点——>左子树——>右子树

中序：左子树——>根节点——>右子树

后序：左子树——>右子树——>根节点

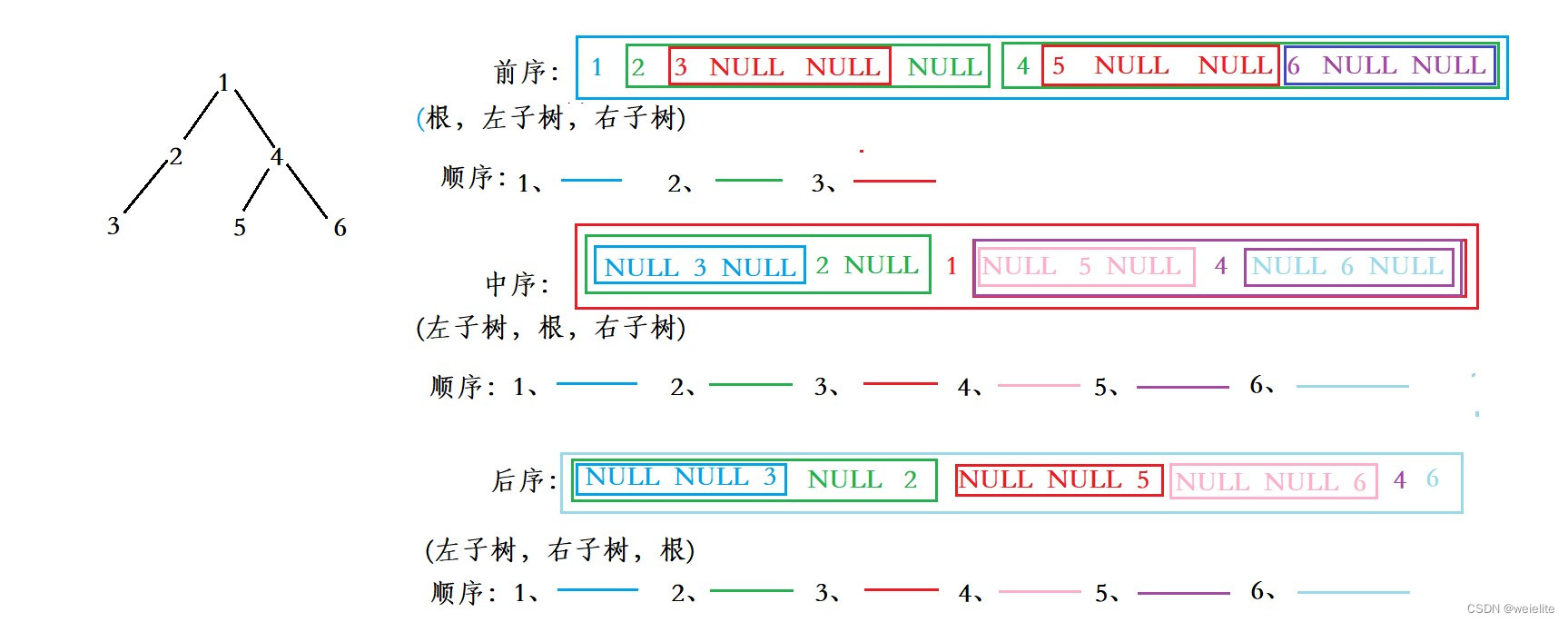
//定义结构
typedef int BTDataType

typedef struct BinaryTree
{
    BTdataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
    BTNode* node=(BTnode*)malloc(sizeof(BTNode));
    if(node==NULL)
    {
        perror("malloc::fail");
        return;
    }
    node->data=x;
    node->left=NULL;
    node->right=NULL;
    return node;
}

//前序遍历
void PrevOrder(BTNode* root)
{
    if(root==NULL)
    {
         return ;   
    }
    printf("%d ",root->data);
    PrevOrder(root->left);
    PrevOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
    if(root==NULL)
    {
         return ;   
    }
    
    InOrder(root->left);
    printf("%d ",root->data);
    InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
    if(root==NULL)
    {
         return ;   
    }
    
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ",root->data);
}

上面就是针对二叉树的遍历

问1：求二叉树的节点的个数

两种方法：1、使用全局遍量(或者在结构中定义一个记录大小的size)

                  2、分治

第一种：使用全局变量

int size=0;
void Treesize(BTNode* root)
{
    if(root==NULL)
    {    
        return ;
    }
    size++;
    Treesize(root->left);
    Treesize(root->right);
}
//但是使用全局变量是不安全的，并且每次运行都必须将size重置，而这又是极为不方便的

第二种：分治

int TreeSize(BTNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
   return TreeSize(root->left)+TreeSize(root->right)+1;
    
}
//从叶子节点开始向根节点累加，在这个过程中将节点统计完成

问2：求二叉树的深度

int TreeHeight(BTNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    
//方法1：每一个上层都不记录下层的数据，在进行比较大小后又需要重新统计结果
    return  TreeHeight(root->left)>TreeHeight(root->right)?
                                TreeHeight(root->left)+1 : 
                                TreeHeight(roo->right)+1;

//方法2：将结果保存下来再判断；
    int left_h=TreeHeight(root->left);
    int right_h=TreeHeight(root->right);
    return left_h>right_h ? left_h+1 : right_h +1;
}

层序遍历：将树进行层序遍历

 前面我们学习了三种遍历方式，层序遍历则是将每一层遍历完再去遍历下一层