题目描述

给你二叉树的根节点 root 和一个整数 limit ，请你同时删除树中所有不足节点，并返回最终二叉树的根节点。

假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为不足节点，需要被删除。

叶子节点，就是没有子节点的节点。

输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

题解

一开始的想法很简答，如果需要经过这个节点的每个路径的节点总和全都比limit小，那么只要我为每个节点算出它经过它的所有路径的总和的最大值，如果这个最大值比limit还要小，那么它就符合条件，应该置为null。

我就写了两次递归，一次递归，把父节点的累加和传递到子节点，然后回传的时候，比较一下最大值，保留最大值。第二次递归，判断每个节点的最大值，如果小于limit，就置为null，这样也能做出来，但是结果非常的差（对应下图第一次提交）。

写的过程中，我也发现上面的做法很冗余，于是想了一下，我们把这颗树简化，抽出某个子树如下。

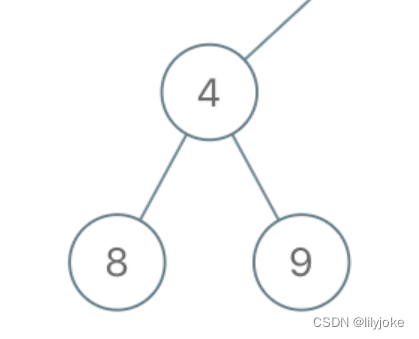
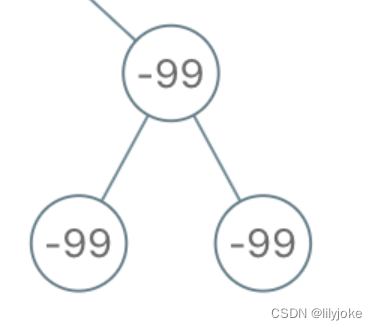
会发现，如果某个父节点的两个叶节点的累加和都小于limit的话，那说明经过它的这两种路径的累加和，都会小于limit，那么这个节点其实就是不足节点。

这样其实就很好做了，下面看下实现。

class TreeNode {
    int val;
    int max = Integer.MIN_VALUE;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }

    public void compare(int max) {
        if (max > this.max){
            this.max = max;
        }
    }
}

class Solution {
    public TreeNode sufficientSubset(TreeNode root, int limit) {
        return computeMax(root, 0, limit);
    }

    public TreeNode computeMax(TreeNode root, int parentSum, int limit){
        int result = parentSum + root.val;
        if(root.left == null && root.right == null){
            if (result < limit){
                return null; //如果叶子节点的累加和小于limit，说明经过这个节点的所有路径的和都小于limit，这个节点就是不足节点。
            } else {
                return root; //反之正常的节点，则返回它本身。
            }
        }

        if (root.left != null){
            root.left = computeMax(root.left, result, limit);
        }

        if (root.right != null){
            root.right = computeMax(root.right, result, limit);
        }

        if (root.left == null && root.right == null){ //如果这个节点的左右叶子节点都是不足节点，那说明经过这个节点的所有路径的和小于limit，它自己也是不足节点。
            return null;
        } else {
            return root;
        }
    }
}