leetcode原题链接：

116题：填充每个节点的下一个右侧节点指针

题目描述

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。

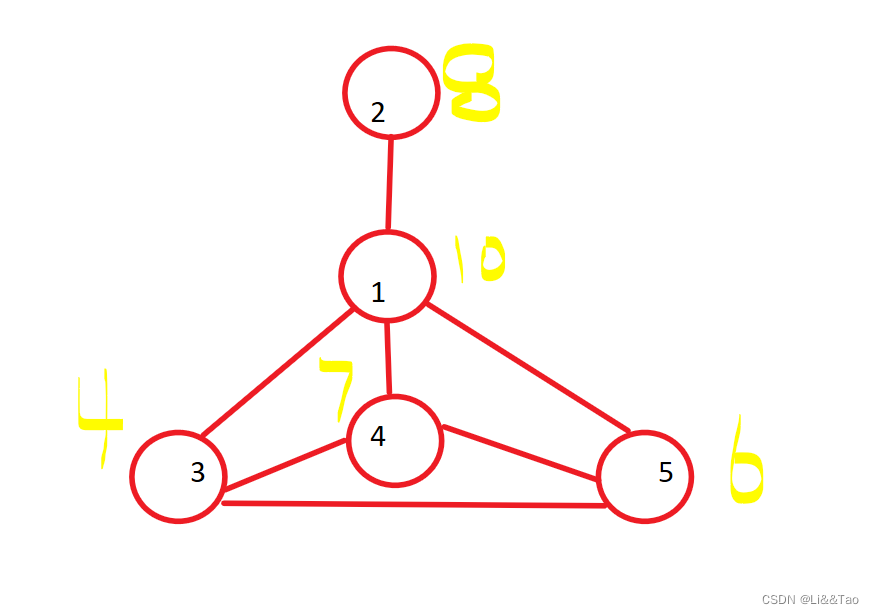
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，‘#’ 标志着每一层的结束。

示例2
输入：root = []
输出：[]

提示：
树中节点的数量在 [0, 212 - 1] 范围内
-1000 <= node.val <= 1000

进阶：
你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

递归解法一

解题思路：
这题在递归中，主要思考点就是，递归左树和右树时。不是同一个头节点的子树时，怎么样把左树链接到右树上去。如上图中五和六节点在递归过程中，这两个点，并没在同一个递归过程中。就无法链接起来，因此我们要修改下递归过程，把左右树同时递归，这样在同一个过程里，就可以看见兄弟节点了。代码演示如下。

  public Node connect(Node root) {
        if(root == null){
            return root;
        }
        process(root.left,root.right);
        return root;
    }

    public void process(Node root1,Node root2){
        if(root1 == null || root2 == null){
            return ;
        }
        root1.next = root2;
        //左树内部链接起来。
        process(root1.left,root1.right);
        //右树内部链接起来
        process(root2.left,root2.right);
        //左树和右树链接起来。
        process(root1.right,root2.left);
      
    }

递归方法二（效率更高）

思路：
我们在递归的过程中，把层级结构也进行递归，每次把层级结构和左树的右节点放进map 中，在遍历到右树时，根据层级来判断，拿到左树，然后把它们相连，就完成了递归。和上面相比，少了一次递归。效率会增加很多.代码演示。

class Solution {
    HashMap<Integer,Node>map = new HashMap();
    public Node connect(Node root) {
        if(root == null){
            return root;
        }
        process(root,0);
        return root;
    }


    public void process(Node root,int level){
        if(root == null || root.left == null){
            return;
        }
        root.left.next = root.right;
        v6(root.left,level + 1);
        v6(root.right,level + 1);
        if(map.get(level) != null){
            Node cur = map.get(level);
            cur.next = root.left;
        }
        map.put(level,root.right);
    }

}