深度学习基础知识-误差反向传播+训练技巧（无代码仅用来理解）

news2024/12/24 2:35:34

参考书籍：（找不到资源可以后台私信我）
《深度学习入门：基于Python的理论与实现 (斋藤康毅)》
《Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition (Aurelien Geron [Géron, Aurélien])》

神经网络正向传播进行的运算在几何学中称为“仿射变换”，即一次线性变换和一次平移，对应的就是加权和与加偏置运算。

在神经网络中，正向传播（forward propagation）是指输入数据通过网络中的每一层，最终产生输出的过程。反向传播（back propagation）是指在网络训练中，通过计算损失函数对网络参数进行更新的过程。

正向时可以通过数值微分计算梯度，反向时直接用链式法则求梯度。前者实现简单，一般不容易出错，但是会慢；后者实现复杂，但是快。可以通过计算两者之差是否够小确认计算是否正确。（梯度确认，gradient check）

反向传播

每次处理一小批数据（mini-batch，比如32个），但是会处理全部训练数据很多次。跑完一遍全部数据称为一个epoch。
正向过程（forward pass）类似预测，就在每层进行计算，然后传递结果到上一层。中间结果需要保留。
计算输出错误（比如用损失函数），并计算每个输出对错误的贡献（error gradients）。继续往下计算，直到达到输入层，这就是反向过程（backward pass）。计算时使用链式法则。
最后使用梯度下降调节所有权重
最开始隐藏层的权重应该是随机的

参数更新

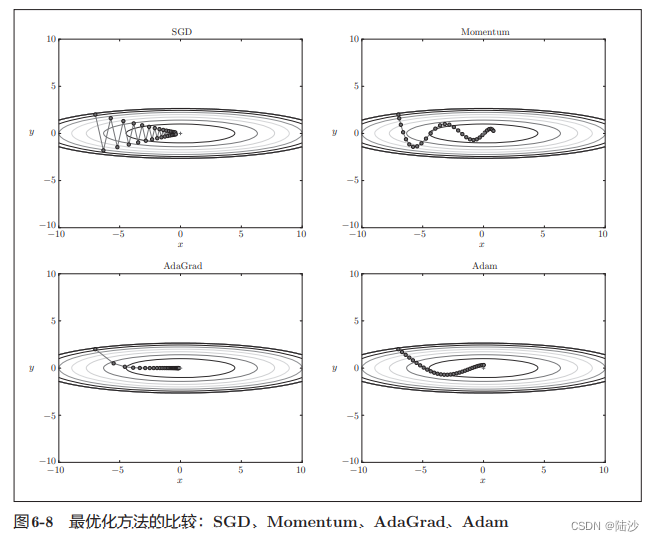
神经网络的学习是为了找到使损失函数值尽可能小的参数，解决这个问题的过程称为最优化（optimization）

为什么SGD会低效？因为梯度的方向并不一定指向最小值方向（所以SGD会沿z形下降），比如函数的形状是非均向（anisotropic），如
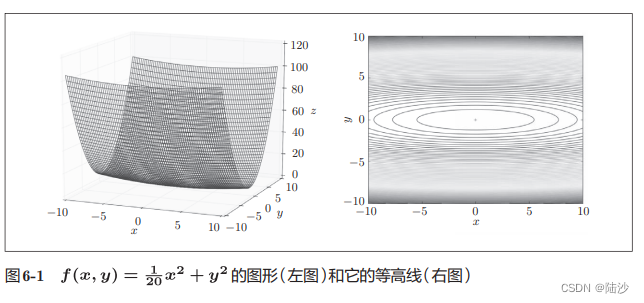
在这里插入图片描述
Momentum（动量）

αv指在不受任何力的时候，物体要逐渐减速（摩擦、空气阻力等原因）。α可能设为0.9之类的值。
momentum的更新路径像小球在碗中滚动，因为虽然x轴受力小，但是一直在受力，所以会向一个方向加速；虽然y轴上受力大，但是会交互地受到正向和反向的力，会抵消，所以会更快向x轴靠近。

AdaGrad
学习的时候为参数的每个元素适当地调整学习率。Ada指Adaptive
在这里插入图片描述
随着学习的深入，更新的幅度会变小。如果无止境地学习，更新量就会变成0，改善的方法之一是使用RMSProp，其思路是逐渐“遗忘”过去的梯度，在做加法运算时将新梯度的信息更多地反映出来。

Adam
融合了Momentum和AdaGrad的优点，并进行超参数的“偏置校正”。其更新过程也类似小球在碗中滚动，但是左右摇晃的程度会减轻一点（因为AdaGrad）。

每种方法都有擅长解决的问题类型。但总体来说，这三种比SGD学习得更快，有时候识别精度也会更高。
在这里插入图片描述

权重的初始值

权重的初始值应该是随机产生的、不同的值。

梯度消失是指在神经网络训练过程中，某些层的梯度变得非常小，甚至趋近于零，导致这些层无法更新参数。这会导致模型无法收敛，训练过程变得非常缓慢，甚至完全停滞不前。

梯度消失通常发生在深度神经网络中，特别是在使用传统的激活函数（如 sigmoid 函数）时。这是因为这些激活函数的导数在输入很大或很小的时候会趋近于零，从而导致梯度变得非常小。为了解决这个问题，研究者们提出了一系列的解决方案，包括使用更加稳定的激活函数（如 ReLU 函数）、使用批量归一化（Batch Normalization）、使用残差连接（Residual Connection）等。

权重初始值可以采用Xavier初始值。（一般深度学习框架已经纳入为标准）。Xavier就是如果前一层节点数为n，则应该使用标准差为1/sqrt(n)的高斯分布初始化权重（这是Caffe等框架中的做法，原始论文中还考虑了下一层输出节点的数量）。
Xavier初始值是以激活函数为线性函数为前提推导出来的，因为sigmoid和tanh函数左右对称，且中央附近可以视作线性函数，所以可以使用Xavier初始值。

如果激活函数使用ReLU时，一般要使用He 初始值：前一层节点数为n时，使用标准差为sqrt(2 / n)的高斯分布初始化权重

Batch Normalization

优点：可以快速学习；不那么依赖初始值；抑制过拟合

思路是调整各层的激活值分布，使其拥有适当的广度。因此，需要向神经网络中插入对数据分布进行正规化的层。
具体来说，就是以进行学习时的mini-batch为单位，使数据分布的均值为0，方差为1。
在这里插入图片描述
前两个公式求均值和方差，第三个公式中加入ε是为了使分母大于0，可以取值1e-7之类的。

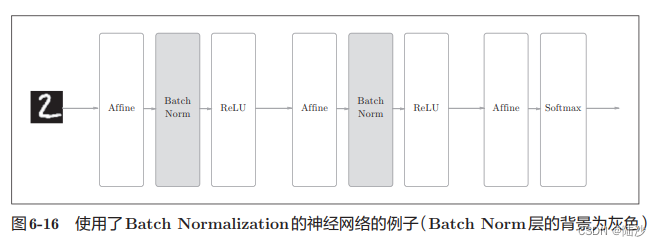
BatchNorm层插入到激活函数前面，激活函数之后再经过一个层，即yi ← γxi + β 其中γ和β的值分别为1和0，后面会通过学习调整到合适的值。

正则化

发生过拟合的原因：模型拥有大量参数、表现力强；训练数据少
权值衰减：在学习过程中对大的权重进行惩罚，以抑制过拟合。比如可以加1/2λW*W（L2范数）到损失函数上。其中λ是控制正则强化度的超参数，越大，对权重施加的惩罚越大。用1/2是为了让求导结果变成λW
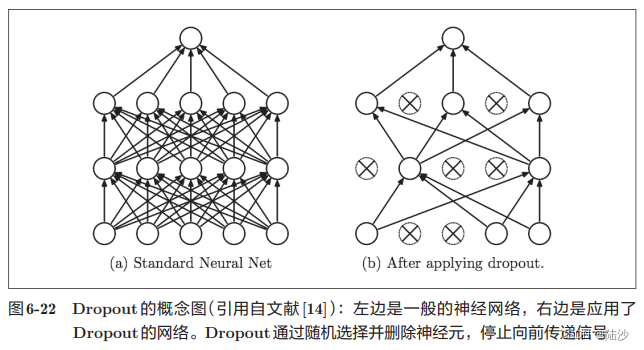
在这里插入图片描述
如果网络模型很复杂，只用权值衰减可能不够，一般使用dropout

class Dropout:
	def __init__(self, dropout_ratio=0.5):
		self.dropout_ratio = dropout_ratio
		self.mask = None
	# 
	def forward(self, x, train_flg=True):
		if train_flg:
			# 随机生成与x形状相同的数组，大于dropout_ratio的设为True
			self.mask = np.random.rand(*x.shape) > self.dropout_ratio
			return x * self.mask
		else:
			return x * (1.0 - self.dropout_ratio)
	
	def backward(self, dout):
		return dout * self.mask