1:点云模型重建
离散点云
• 数据量大
• 渲染显示大
• 模型操作计算不方便
网格模型
• 数据量小
• 渲染方便
• 模型操作计算方便
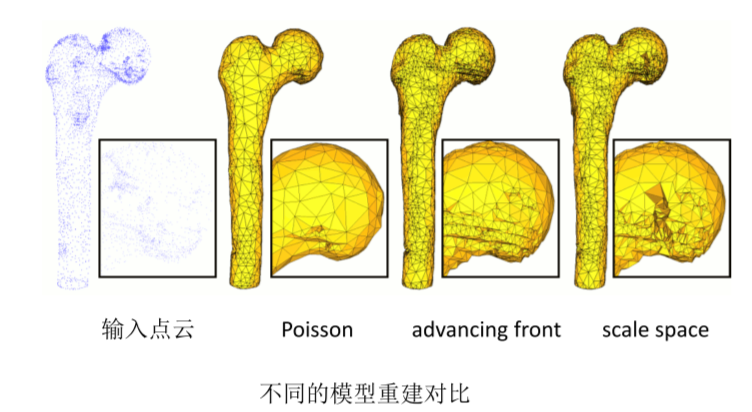
重建步骤

2:凸包算法
凸包
• 平面凸包:平面的一个子集S被称为是“ 凸”的,当且仅当对于任意两点 p, 𝑞 ∈ 𝑆 ,线段𝑝𝑞都完全属于S。
• 二维的凸包称为凸多边形,三维的凸包称
为凸多面体。
应用
• 碰撞避免
• 计算最小包围盒
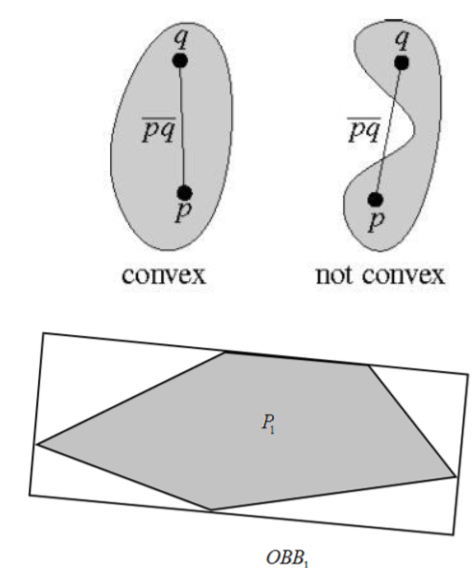
二维凸包算法
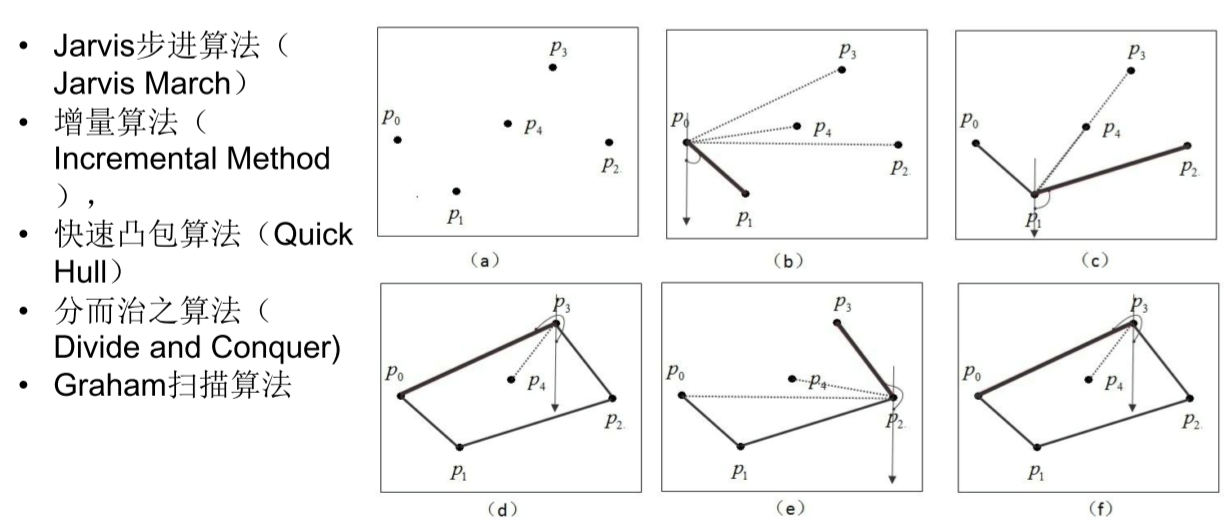
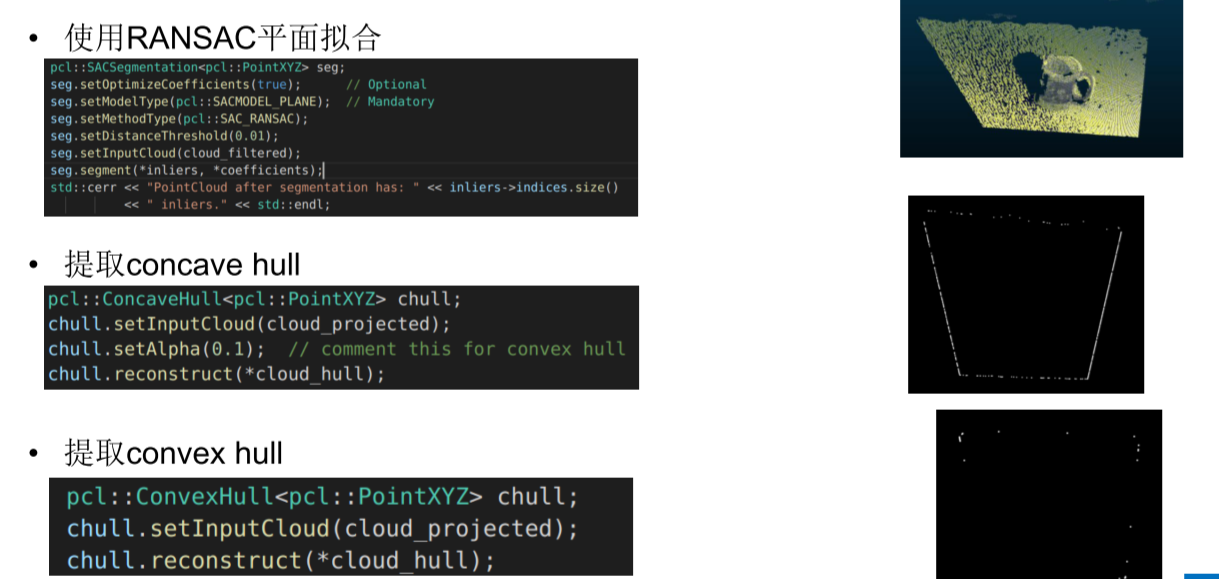
三维算法

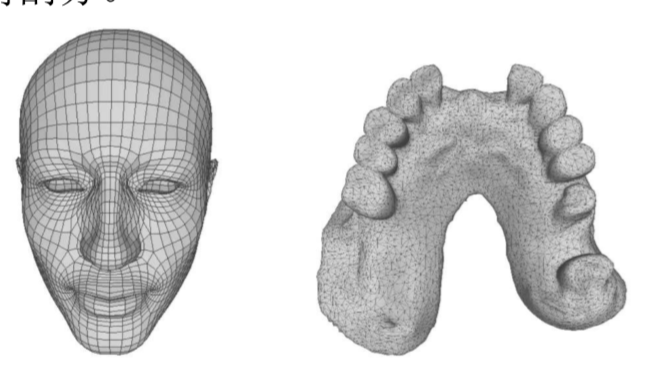
点云网格化
点云网格化就可以把点云转换为mesh模 型
• 三角形表示网格也叫三角剖分。
• 三角网格稳定性强。
• 三角网格比较简单(主要原因),
实际 上三角网格是最简单的网格类型之一, 可以非常方便并且快速生成,在非结构 化网格中最常见。而且相对于一般多边 形网格,许多操作对三角网格更容易。
• 有助于恢复模型的表面
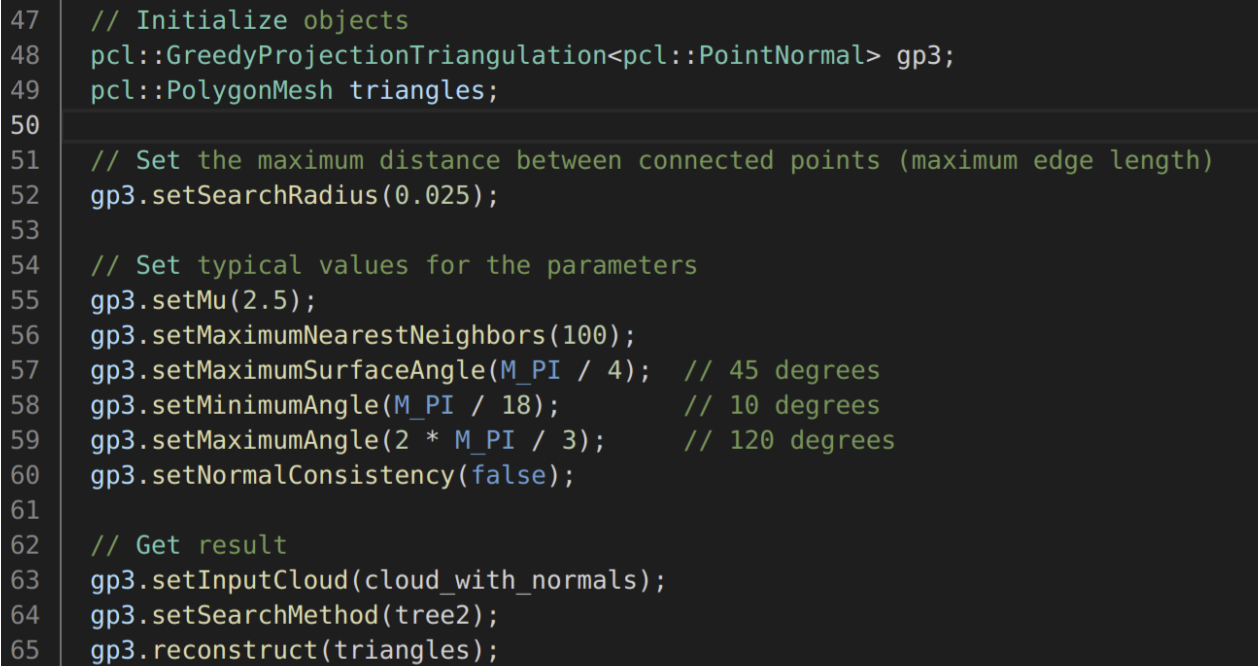
点云贪心三角化原理
贪心三角化法:pcl::GreedyProjectionTriangulation • 可处理来自一个或者多个设备扫描到得到、并且 有多个连接处的散乱点云。
• 适用于采样点云来自表面连续光滑的曲面,并且 点云的密度变化比较均匀的情况
• 贪心投影三角化的大致流程是这样的: • 将点云通过法线投影到某一二维坐标平面内 • 对投影得到的点云做平面内的三角化,从而得到 各点的拓扑连接关系。
• 最后根据平面内投影点的拓扑连接关系确定各原 始三维点间的拓扑连接,所得三角网格即为重建
得到的曲面模型

点云贪心三角化原理
B样条曲线(B-spline curves)

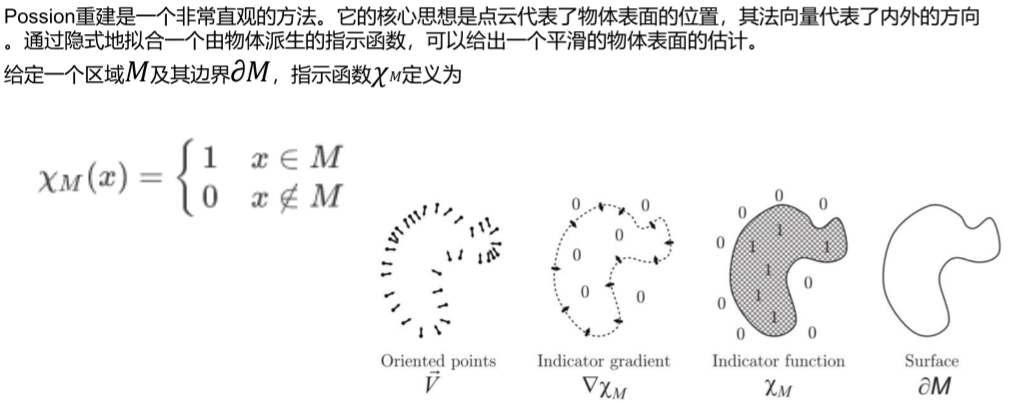
Poisson 重建
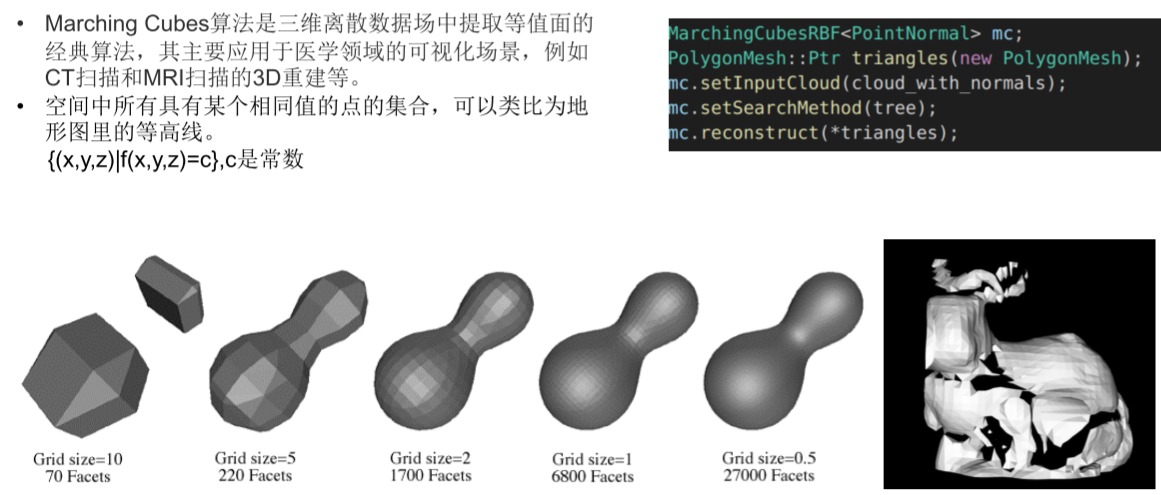
Marching Cube
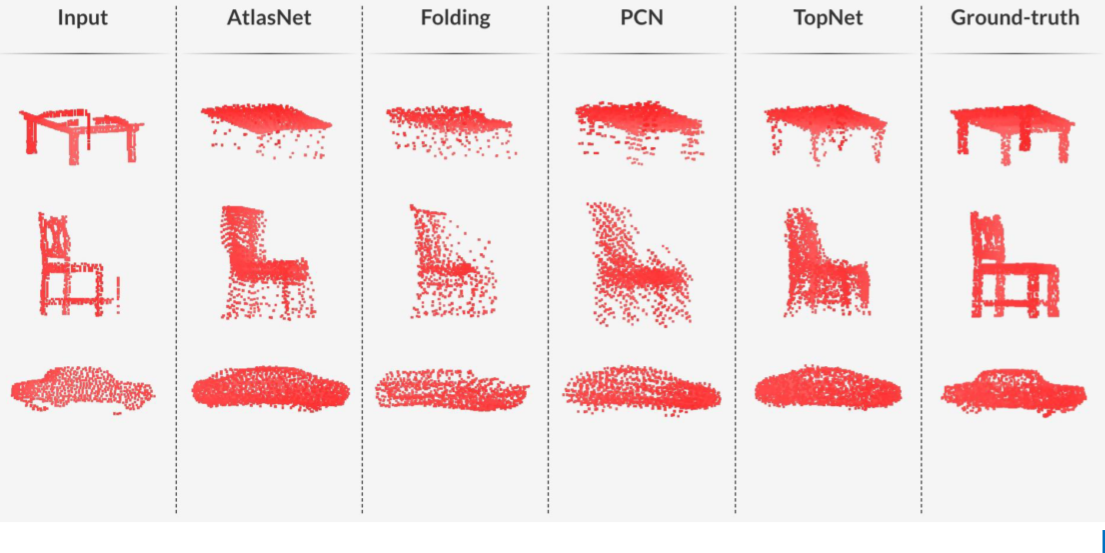
点云补全