n 个小区排成一列，编号为从 0 到 n-1 。一开始，美团外卖员在第0号小区，目标为位于第 n-1 个小区的配送站。
给定两个整数数列 a[0]~a[n-1] 和 b[0]~b[n-1] ，在每个小区 i 里你有两种选择：
1) 选择a：向前 a[i] 个小区。
2) 选择b：向前 b[i] 个小区。

把每步的选择写成一个关于字符 ‘a’ 和 ‘b’ 的字符串。求到达小区n-1的方案中，字典序最小的字符串。如果做出某个选择时，你跳出了这n个小区的范围，则这个选择不合法。
• 当没有合法的选择序列时，输出 “No solution!”。
• 当字典序最小的字符串无限长时，输出 “Infinity!”。
• 否则，输出这个选择字符串。

字典序定义如下：串s和串t，如果串 s 字典序比串 t 小，则
• 存在整数 i ≥ -1，使得∀j，0 ≤ j ≤ i，满足s[j] = t[j] 且 s[i+1] < t[i+1]。
• 其中，空字符 < ‘a’ < ‘b’。

---

简述：现有一个整数n，及两个长度为n的数组num1和num2，每个数组中的元素i表示能够在当前位置移动的距离(正/负)，每次在位置i移动时可以选择num1[i]或num2[i]，要求通过选择num1和num2来移动，最终到达n-1的位置，其中使用"a"和"b"分别表示选择的数组，最终得到一个字符串s，返回最小字典序的s，其他情况：若最小字典序无限长则返回"Infinity!"，若不能到达n-1位置则返回"No solution!"

思路：

首先理解题意，现在需要返回三种值：s，"Infinity!"和"No solution!"：

① s和"No solution!"：当能到达n-1位置并返回最小字典序s，不能到达返回"No solution!"；（解决，能过90%样例）

② "Infinity!"：需要能够到达n-1的位置，同时s为最小字典序，且路径中有环；(本题难点，刚开始没理解为什么有环还能到终点，不应该在环里循环出不去吗，画了个图才理解)

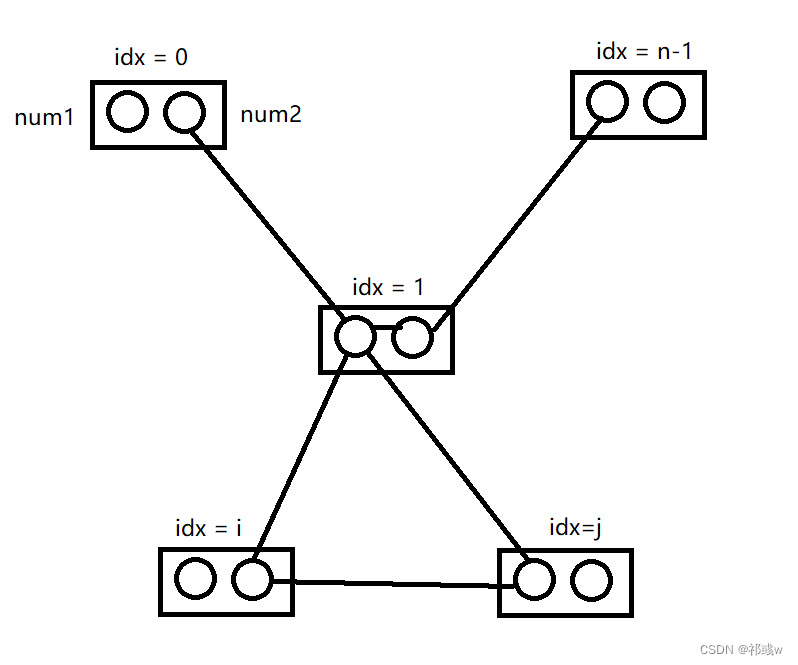
简单讲就是，由于每个位置有两个选择，所以即使其中一个选择遇到环，最终也能在该位置通过选择另一个选择来跳出环（如果两个选择都是环，那就是不可达"No solution!"）。

1、选择DFS算法求解；

2、设定一个全局数组来记录当前位置选择过几遍，来解决是否存在环的问题；

3、对于最小字典序，在DFS里将选择"a"的数组放在选择"b"的数组上面，就可以保证最终得到的是最小字典序（可以这样理解，由于有两个数组，所以可以看做成一个二叉树遍历，把"a"放在上面表示先序遍历，而先序遍历先遍历根"a"，然后左子树"a"，最后右子树"b"，可能理解有误欢迎交流讨论）；

代码：

import java.util.*;

public class Main {
    
    private static StringBuilder ans = new StringBuilder(); // 记录字典序最小字符串
    private static int[] a; // 数组a
    private static int[] b; // 数组b
    private static int[] visit; // 记录是否经过当前位置
    private static boolean loop = false; // 判断是否有环
    
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int len = in.nextInt();
        a = new int[len];
        b = new int[len];
        visit = new int[len];
        
        for(int i = 0; i < len; i++){
            a[i] = in.nextInt();
        }
        for(int i = 0; i < len; i++){
            b[i] = in.nextInt();
        }
        
        if(dfs(0, len-1)){
            if(loop){ // 能到达存在环
                System.out.println("Infinity!");
            }else{ // 能到达不存在环
                System.out.println(ans);
            }
        }else{ // 不能到达
            System.out.println("No solution!");
        }
        
    }
    
    // 输入当前位置及最终位置，返回是否到达终点
    public static boolean dfs(int cur, int target){
        // 边界判断
        if(cur < 0 || cur > target){
            return false;
        }
        // 条件判断
        if(cur == target){
            return true;
        }
        // 是否存在环
        if(visit[cur] > 0){
            visit[cur]++;
            return false;
        }
        visit[cur]++; // 记录当前位置访问次数

        /*
           选择"a"的过程，先添加字符，然后判断当前位置能否到达终点，
           如果能到达返回true，能到达的同时如果当前位置访问次数大于1，说明该位置存在环。
           如果不能到达，则删除"a"，去判断"b"
        */
        ans.append("a");
        if(dfs(cur+a[cur], target)){
            if(visit[cur] > 1){
                loop = true;
            }
            return true;
        }
        ans.deleteCharAt(ans.length()-1);
        
        ans.append("b");
        if(dfs(cur+b[cur], target)){
            if(visit[cur] > 1){
                loop = true;
            }
            return true;
        }
        ans.deleteCharAt(ans.length()-1);
        
        // "a"和"b"都不能到达，返回false
        return false;
    }
    
}