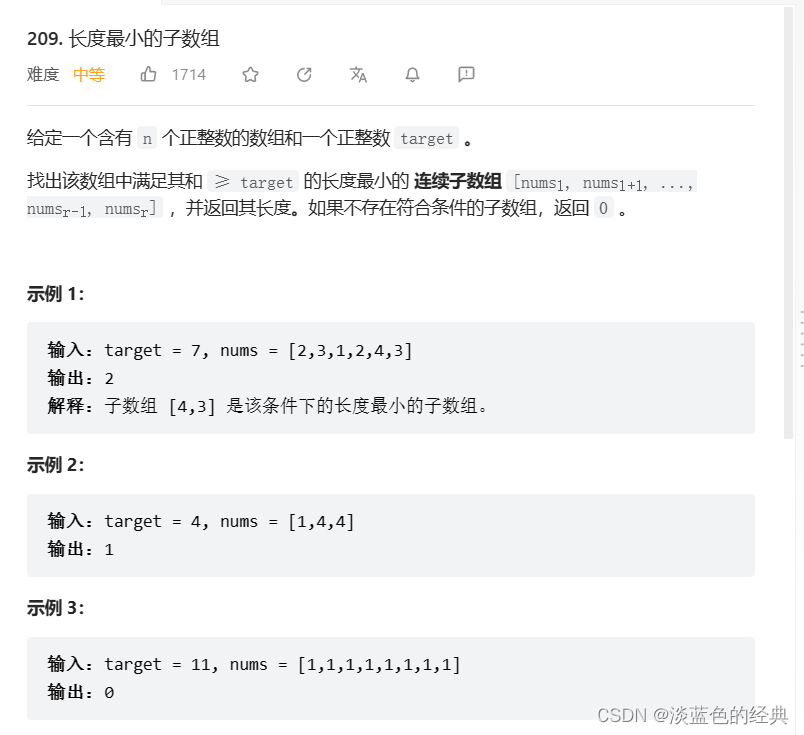
问题描述

方法一：暴力求解

暴力求解法：时间复杂度O(n^2)，空间复杂度O(1)。
暴力求解法的思想：每一次遍历数组，然后更新result的值，一个for循环作为起始位置，一个for循环作为终止位置，用两个for循环完成了不断搜索区间的过程。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
        int result=INT_MAX;
        int sum=0;
        int sublenght=0;
        for(int i=0;i<nums.size();i++)
        {
            sum=0;
            for(int j=i;j<nums.size();j++)
            {
                sum+=nums[j];
                if(sum>=target)
                {
                    sublenght=j-i+1;
                    result=min(result,sublenght);
                    //result=result<sublenght?result:sublenght;
                    break;
                }
            }
        }
        return result==INT_MAX?0:result;
    }
};

方法二：滑动窗口

时间复杂度：O(n),空间复杂度O(1)，为什么时间复杂度为O(n)呢？原因是每个元素之遍历了一次，而暴力求解每个元素遍历了两次。

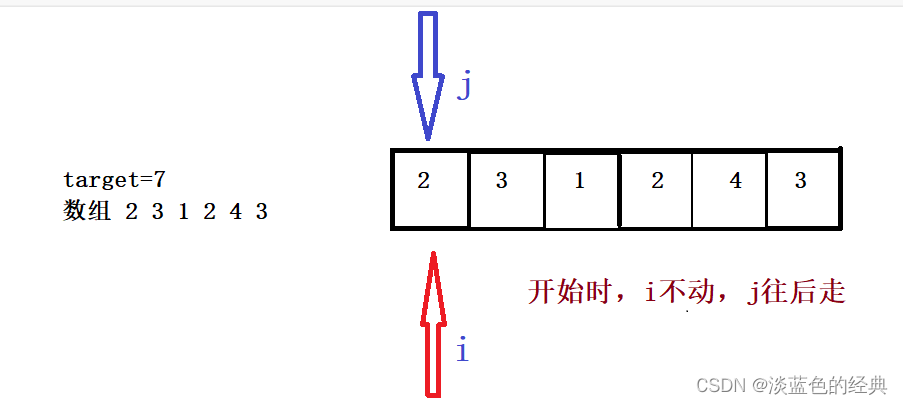
思路：不但调节起始位置和终止位置，从而得出我们想要的结果。
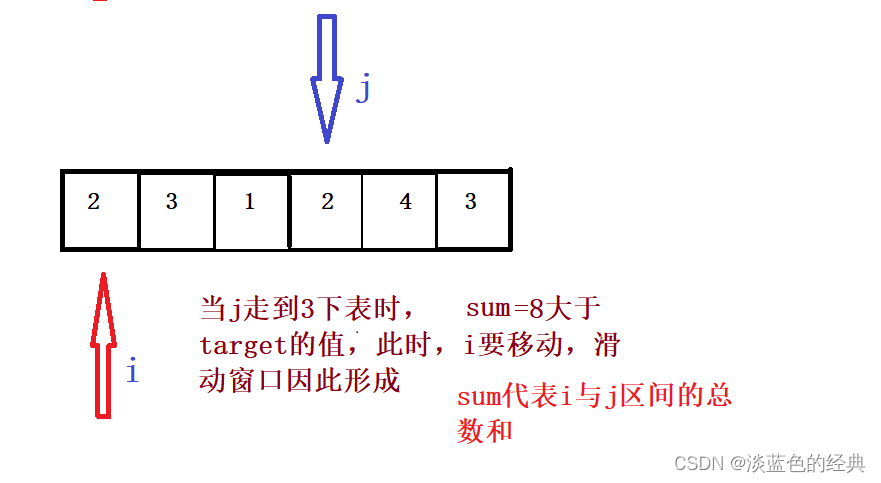
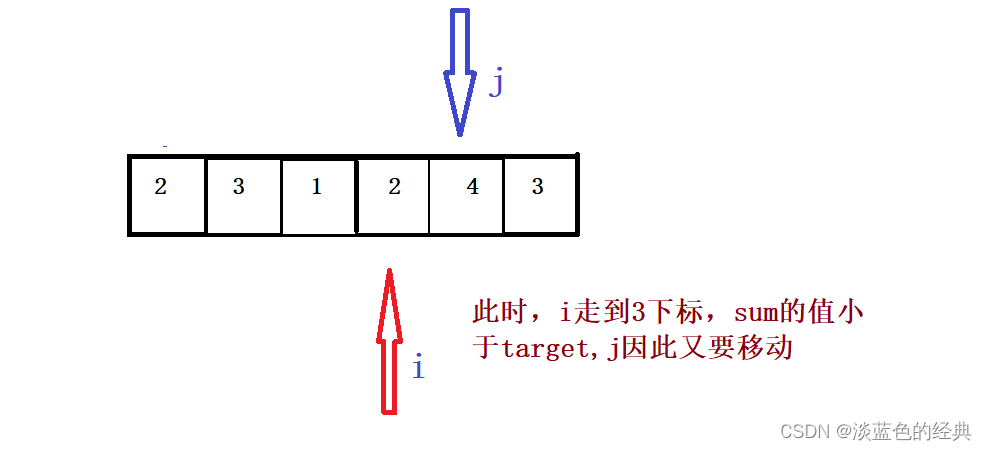
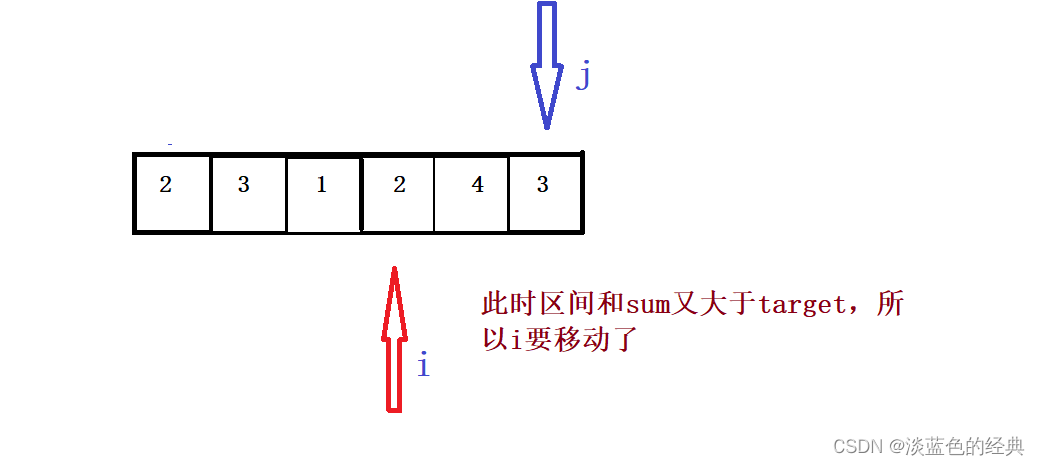
那么for循环里面是起始位置还是终止位置呢？此时我们需要探讨，如果for循环里面是起始位置，那么又会陷入暴力求解，所以我们将终止位置j放入for循环里面，而在for循环的里面我们设置起始位置，从而形成了滑动窗口。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
        int sum=0;
        int sumL=0;
        //滑动窗口
        int result=INT_MAX;
        int j=0;
        int i=0;
        for(j=0;j<nums.size();j++)
        {
           sum+=nums[j];
           while(sum>=target)
           {
               sumL=j-i+1;
               sum=sum-nums[i];
               result=min(result,sumL);
               i++;
           }
        }
        return result==INT_MAX?0:result;
    }
};