红黑树 C++

企业里永远是技术驱动理论发展

比起理解红黑树的原理，更重要的是理解红黑树的应用场景，因为某些应用场景的需要，红黑树才会应运而生。

红黑树的特点：

插入，删除，查找都是O(logn)的复杂度。

红黑树的应用：

epoll的实现，内核会在内存开辟一个空间存放epoll的红黑树，并将每个epollfd加入到红黑树中，一般epoll会设置LT水平触发，当网卡有数据到来，可读缓冲区不为空，会触发回调EPOLLIN事件，而之前注册了对EPOLLIN事件感兴趣的socketfd会有专门的队列存储，内核会遍历队列搜寻对应的socketfd，因为在红黑树里找有近似O(logn)的时间复杂度，所以10亿个socket也只需要20次查找。
进程调度，内核CFS队列，以红黑树的形式存储进程信息。
有的hashtable（记得是java），当冲突时不以链表来组织重复元素，而是以红黑树的形式来组织。
内存管理，比如空闲链表freelist可以通过红黑树来组织，这样malloc的时候要找到符合大小的内存块，如果不是firstfit的原则，而是全局最优大小原则，想找到适合的内存块就可以通过红黑树来找。
Nginx的Timer事件管理。

红黑树定义

写代码之前先写一下红黑树的规则吧

每个颜色不是红就是黑。
根节点必黑
叶子节点必黑
红色节点的左右孩子都为黑
每个节点到其叶子节点（nil）的所有路径上的黑色节点数量都一样

我的理解：从任一节点到叶子结点的路径上，路径的元素必然有黑色节点，而路径的长度则取决于路径上红色节点的数量，最短的路径上，所有节点都是黑色，这种情况下，查找效率为真实的O(logn)，和严格平衡的AVL树一致。而如果在刚刚的最短路径上，也就是所有黑色节点的中间插入红色节点，这样是不会打破红黑树的平衡的(规则5)，此时便是最长路径，查找效率为2logn，但依然和logn在同一数量级，因此，红黑树的查找效率可以看做是(Ologn)，同时比AVL树拥有更高的插入和删除效率。

红黑树代码框架

//-既然标题是c++，那么就写成满满的c++风格吧
using Color = bool;//-颜色因为只有红或者黑，选择bool类型
using KEY_TYPE = int;//-为了更好理解红黑树，就不写成模板类了，所以首选万年int（笑~）
using VALUE_TYPE = int;//-同理

//-全局静态红黑变量
static const Color red = false;
static const Color black = true;

//-红黑树的节点特点，有color，有parent
class RBtree_node{
public:
Color color;
RBtree_node * parent;
RBtree_node * left;
RBtree_node * right;

KEY_TYPE key;//-后期如果想解耦合，可以将key和value抽离出去
VALUE_TYPE value;
RBtree_node(Color color_):color(color_),parent(nullptr),left(nullptr),right(nullptr),key(-99999){}
RBtree_node(Color color_, KEY_TYPE key_,RBtree_node * nil):
color(color_),parent(nil),left(nil),right(nil),key(key_){}
};


class RBtree{
private:
//-红黑树数据成员：其中nil的意义在于，因为红黑树的所有叶子节点都是黑色的，所以可以将所有临近末尾的节点，
//-都连接到这一个叶子结点nil上，同理，root的parent也可以连接到nil上，形成一个dummy空节点
RBtree_node * root;
RBtree_node * nil;
public :
//-以下实现了红黑树常用接口：
//-构造函数
RBtree(){
nil = new RBtree_node(black);//-为所有叶子节点nil初始化，颜色为黑色
root = nil;//-红黑树为空的时候，让nil作为root
}
//-左旋
void leftRotate(RBtree_node *left_node);

//- 右旋
void rightRotate(RBtree_node * right_node);

//-插入key
void insertNode(KEY_TYPE key);

//-修复插入
void fixInsert(RBtree_node * node);

//-查找某个key的节点
RBtree_node* searchNode(KEY_TYPE key);

//-查找某个节点的中序后继
RBtree_node* successor(RBtree_node * node);

//-删除key
void deleteNode(KEY_TYPE key);

//-修复删除
void fixDelete(RBtree_node * node);

//-层序遍历打印红黑树
void print();

//-打印中序遍历
void printMiddle(RBtree_node * node);

};

接下来将接口一一实现：

红黑树节点左旋右旋：

实现参照该图，至于学习方法也没啥捷径，只能把这个结构图和变换方式深深印刻在脑海里。

手撕代码的时候想象一下还是容易写的，如果觉得这样很累就纸上画个草图。

由于左旋和右旋是对称的，所以规则只需要记一半。

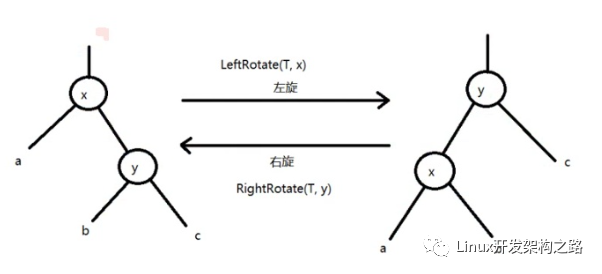
图1 左旋右旋

//-左旋

void RBtree::leftRotate(RBtree_node *left_node){

RBtree_node * right_node = left_node->right;
//-右节点的左枝条接在左节点的右枝条上
left_node->right = right_node->left;
if(right_node->left!=nil){
left_node->right->parent = left_node;
}
//-右节点接在左节点的父亲上
right_node->parent = left_node->parent;
if(left_node == root){
//-nil不会指向任何节点，但是root->parent是nil
root = right_node;
}
else if(left_node == left_node->parent->left){
left_node->parent->left = right_node;
}else{
left_node->parent->right = right_node;
}
//-左节点接在右节点的左枝上
left_node->parent = right_node;
right_node->left = left_node;
}

//- 右旋：写完左旋后，把所有left和right对调即可
void RBtree::rightRotate(RBtree_node * right_node){
RBtree_node * left_node = right_node->left;
right_node->left = left_node->right;
if(left_node->right!=nil){
right_node->left->parent = right_node;
}
left_node->parent = right_node->parent;
if(right_node == root){
root = left_node;
}
else if(right_node == right_node->parent->right){
right_node->parent->right = left_node;
}else{
right_node->parent->left = left_node;
}
right_node->parent = left_node;
left_node->right = right_node;
}

红黑树的插入，插入修复

插入的步骤原理：

找到插入位置，注意红黑树新节点的插入位置都是叶子结点。
如果红黑树中没有节点，插入节点需要改变root指向，同时将root的parent指向nil。
改变插入节点父亲的左右指针，同时插入节点本身的左右指针指向nil。
如果插入节点的父亲是红色，说明平衡被打破了，需要执行修复插入，让红黑树恢复平衡

要点:

如果在查找的时候发现元素已经存在，我这里就直接抛弃了新元素的插入，如果要实现红黑树multimap的insert_equal功能可以自己实现一下。
为什么要插入修复？

首先我们会强制默认所有的新节点都是红色节点。

因为红色节点不论插在哪个位置，都不会破坏规则5（路径上黑色节点数量相同），唯一可能破坏的是规则4（红色节点的孩子必黑），由于破坏规则5比破坏规则4要容易得多，所以将新节点设置为红色可以尽量地避免破坏规则。

当新的红色节点插入到一个红色节点之后，破坏了规则4，才需要修复，如图2，插入元素16

修复的意义和规则在于，如何将新红节点的父亲（34）变成黑色后，依然能保持红黑树的左右平衡，这个时候才涉及到对伯父节点（184）的讨论

插入修复的步骤原理：

我们的目的是为了让左边cur为红的情况下，使父亲变黑且不会破坏平衡。
所以只要cur的parent是红色，就一直循环。
判断伯父节点（184），如果伯父节点是红色，如图2，那么同时将父亲和伯父改成黑色就不会改变平衡，将祖父（101）变红，让cur变成祖父（101）进入下一轮迭代。

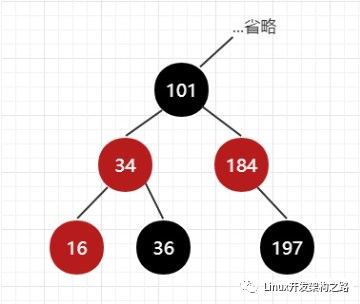
图2 伯父（184）为红

如果伯父节点是黑色，如图3，插入节点16

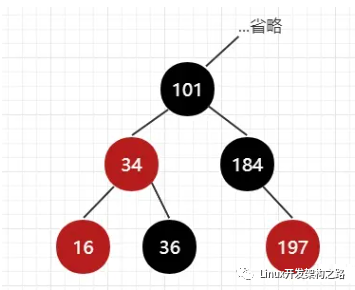
图3 伯父（184）为黑

那么将父亲（34）变黑就会让左边多一个黑色，不过可以通过让祖父（101）变红，旋转祖父，让祖父下沉，父亲上浮，这样相当于让老爹变黑同时左右都加了一个黑色，不会破坏平衡。

但是旋转祖父需要有个前提条件，插入节点不能是父亲的靠内节点，如图4，插入节点（36）为右孩子，父亲（34）是祖父（101）左枝。

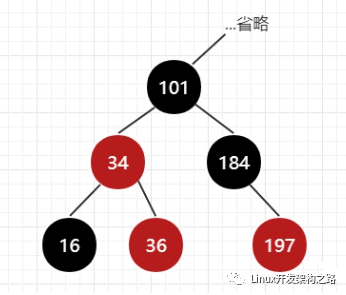
图4，插入节点（36）是靠内节点

一旦右旋祖父（101），就会破坏cur（36）和父亲（34）的连接关系，所以必须要把cur从靠内节点变成靠外节，一个方便的方式是让父亲成为新cur（34），并右旋cur（34），如图5，之后再进行上个步骤，将新父亲（36）变黑，祖父（101）变红，右旋祖父。

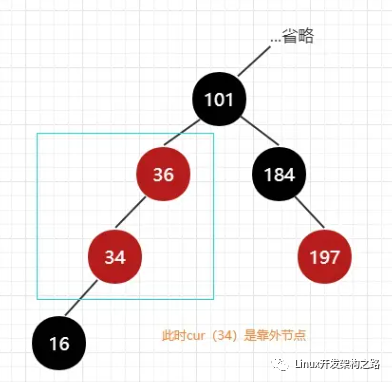
图5 原cur（36）经过旋转变为父亲，将34作为新cur

要点：

终止条件，当当前节点（红）的父亲为黑的时候打破循环（注意回溯到nil的时候的，nil也是黑色）
终止循环后，注意如果回溯到root，会改变root的颜色为红，需要在循环结束后fix成黑色。
因为父亲是祖父左枝也好右枝也好，变换总是左右对称的，所以规则只需要记一半。

//-插入key
void RBtree::insertNode(KEY_TYPE key){
RBtree_node * prev = nil;
RBtree_node * cur = root;
while(cur!=nil){
prev = cur;
if(key>cur->key){
cur = cur->right;
}else if(key<cur->key){
cur = cur->left;
}else{//-该key已经存在
return;
}
}
//-创建新节点
RBtree_node * new_node = new RBtree_node(red,key,nil);
//-如果节点没有元素
new_node->parent = prev;
if(prev == nil){
root = new_node;
}
else if(key<prev -> key){
prev ->left = new_node;
}else{
prev ->right = new_node;
}
fixInsert(new_node);
print();
}

//-修复插入
void RBtree::fixInsert(RBtree_node * new_node){
while(new_node -> parent->color == red){//-终止条件要注意
//-如果父亲是左枝
if(new_node->parent == new_node -> parent->parent->left){
//-获得其伯父节点
RBtree_node * uncle = new_node->parent->parent->right;
if(uncle->color == red){//-如果伯父是红色，那么将父亲和伯父同时变黑，不会破坏左右平衡
uncle->color = black;
new_node->parent->color = black;
new_node->parent ->parent->color = red;//-将祖父变红，才能实现下一轮回溯修复
new_node = new_node->parent->parent;
}else{//-如果伯父是黑色
//-判断new_node是不是右孩子，如果是右孩子转换成左孩子
if(new_node == new_node -> parent->right){
new_node = new_node->parent;
leftRotate(new_node);
}
//-此时红色节点是左孩子
//-如果结构本是平衡状态，右边本该比左边多一个黑，但是我们将父亲（左)变黑会破坏平衡，
//-所以需要右旋祖父，把父亲上浮，相当于在左枝多一个黑的时候给右枝也多了黑，这样左右就能平衡
new_node->parent->color = black;
new_node->parent ->parent->color = red;
rightRotate(new_node->parent->parent);
}
}
//-如果父亲是右枝（将上边代码的left和right全部对调即可，不用记规则）
else {
RBtree_node * uncle = new_node->parent->parent->left;
if(uncle->color == red){//-如果伯父是红色
uncle->color = black;
new_node->parent->color = black;
new_node->parent ->parent->color = red;
new_node = new_node->parent->parent;
}else{//-如果伯父是黑色
if(new_node == new_node -> parent->left){
new_node = new_node->parent;
rightRotate(new_node);
}
new_node->parent->color = black;
new_node->parent ->parent->color = red;
leftRotate(new_node->parent->parent);
}
}
}
//-如果new_node回溯到root，此时root->parent==nil（black）打破了循环，而此时root被改变成了黑色，违反了规则1，
//-所以最后需要强行把root fix成黑色
root->color = black;
}

红黑树查找某个key，以及找到某个节点的中序后继

主要讲下怎么根据当前节点找中序后继，根据BST的特性

如果当前节点有右孩子：其后继肯定在右枝条上，且是右枝条最左边的元素。
如果当前节点没有右孩子：根据中序遍历的递归顺序，假设cur是其父亲的左孩子，cur遍历完后，下一个节点（后继）就是父亲，反之，如果cur是右孩子，说明其父亲也递归完了，需要回溯父亲的父亲，所以只需要一直往上找直到cur为其parent的左孩子为止，然后返回parent，而回溯到root的时候，root的父亲虽然是nil，但是nil是没有左右孩子的，所以退出循环。

//-查找某个key的节点
RBtree_node* RBtree::searchNode(KEY_TYPE key){
RBtree_node * cur = root;
while(cur!=nil){
if(key>cur -> key){
cur = cur->right;
}else if(key < cur -> key){
cur = cur->left;
}else{
return cur;
}
}
return cur;
}

//-查找某个节点的中序后继
RBtree_node* RBtree::successor(RBtree_node * node){
//-如果节点有右孩子
if(node->right!=nil){
RBtree_node * res = node -> right;
while(res->left!=nil){
res = res->left;
}
return res;
}else{
while(node!=root&&node!=node->parent->left){
node = node->parent;
}
return node->parent;
}
}

红黑树删除，修复删除

删除的步骤原理：

类似二叉堆，当我们从栈顶pop元素后，需要用二叉树末尾节点代替原来的root，而后从二叉堆顶部开始向下修复，同理，我们要删除树上的一个节点，自然需要一个节点来顶替删除节点(key_node)的位置，因次，我们并不一定要在数据结构上真正删除key_node，可以找到那个顶替节点(delete_node)，将顶替节点的数据覆盖key_node，而在数据结构上真正删除的是那个顶替节点（delete_node）。
在数据结构上真正删除哪个节点（delete_node怎么取），取决于(key_node)是否有左右枝条，
如果key_node左右孩子都没有，说明是叶子节点，直接删除key_node即可，delete_node就是key_node本身。
如果key_node左右孩子只有其一，那么删除key_node只需要将孩子接在祖父上，删除自己即可，所以delete_node依旧是key_node本身。
如果key_node左右孩子都有，那么可以根据上面的successor函数，找到key_node的直接后继，也就是删除节点右边最小的元素，将其本身数据用来顶替key_node，不会破坏BST的性质。之后将其作为delete_node在数据结构上删除即可，如图6。

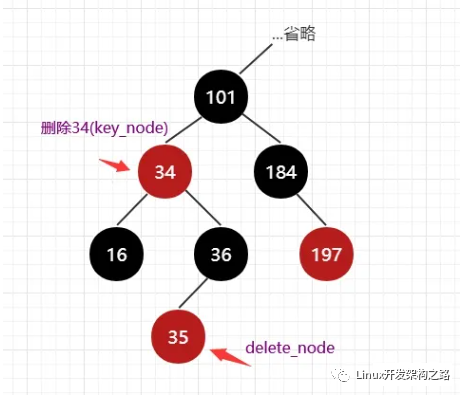
图6

找到delete_node后，还要找到delete_node的孩子（delete_son），将delete_son接在delete_node的父亲上。

判断delete_node是否是黑色，如果是黑色，则删除了该元素必会破坏红黑树的平衡（规则5），需要修复fix_delete，而修复从delete_son开始。

要点：

记得额外判断如果delete_node是root的情况，需要更新其孩子delete_son为新的root。

修复删除的步骤原理：

删除节点delete_node如果是黑色的，说明树中有一个枝条（假设是左枝）的黑色节点必会比兄弟枝条（右枝）少一个。我们怎么才能使左右重新平衡，要么让左枝条黑色节点+1，要么让右枝条黑色节点-1。后续步骤全都以delete_son为其父左枝条为例，因为对称，依旧只需要记一半的规则。
让delete_son的兄弟bro变成黑色，如果bro是红色，则bro->黑色，parent->红色，左旋parent，此时bro的左枝会变成新的bro，因为bro是红色，所以根据规则4，左枝必为黑，即新bro变为黑色。
判断bro的孩子，
如果左黑右黑，将bro->红色，不会改变bro后续孩子的平衡，同时，bro所在的右枝条的黑色节点-1，红黑树重新平衡，将父亲作为新的delete_son继续循环，直到delete_son为红色。
如果左红右黑，通过右旋bro，变成左黑右红。
如果左黑右红。bro继承父亲的颜色，将bro的父亲变黑，右孩子变黑（右枝黑+1），左旋父亲（左枝黑+1，右枝黑-1），总的来说delete_son所在的左枝条的黑色节点+1，红黑树重新平衡，并且直接让delete_son=root退出循环。

要点：

终止条件：当delete_son==root或者delete_son为红的时候终止循环。

//-删除key
void RBtree::deleteNode(KEY_TYPE key){
//-查找key所在节点
RBtree_node * key_node = searchNode(key);
//-实际删除的节点
RBtree_node* delete_node;
//-delete_node的孩子
RBtree_node* delete_son;
//-如果同时有左枝或者右枝条
if(key_node->left != nil&&key_node->right != nil){
delete_node = successor(key_node);
delete_son = delete_node->right;
}//-如果仅有左枝或者右枝条或者左右都没有
else{
delete_node = key_node;
if(key_node->left != nil){
delete_son = key_node->left;
}else{
delete_son = key_node->right;
}
}

//-删除deletenode
delete_son->parent = delete_node->parent;
//-先判断deletenode是不是根节点
if(delete_node == root){
root = delete_son;
}
else if(delete_node == delete_node->parent->left){
delete_node->parent->left = delete_son;
}else{
delete_node -> parent -> right = delete_son;
}
//-覆盖key_node原有数据
key_node->key = delete_node -> key;
key_node ->value = delete_node -> value;

//-如果删除节点是黑色的，需要修复delete_son,注意是孩子
if(delete_node->color == black){
fixDelete(delete_son);
}
//-释放空间
delete delete_node;
//-打印
print();
}

//-修复删除
void RBtree::fixDelete(RBtree_node * delete_son){
//-修复的原因是因为delete_son所在的枝条的黑节点比另一个枝条少一个，所以不平衡，所以需要填上左边缺失的黑，或者减掉右边多余的黑
//-当delete_son是黑色的一直循环
while(delete_son!=root&&delete_son->color == black){
//-判断delete_son所在枝条,如果是左枝
if(delete_son == delete_son->parent->left){
//-如果兄弟是红色的
RBtree_node * bro = delete_son->parent->right;
if(bro->color == red){
bro->color = black;//-兄弟变黑
delete_son->parent->color = red;//-父亲变红
leftRotate(delete_son->parent);//-左旋父亲，兄弟上浮，相当于左右都加了一个黑，不改变平衡状态
bro = delete_son->parent->right;//-新的bro是原来bro的左枝，因为原bro是红的，其左右枝都是黑色的，这样保证新的兄弟是黑色的
}
//-此时兄弟是黑色的,判断兄弟的孩子
//-左黑右黑（兄弟的孩子平衡了）
if(bro->left->color == black&&bro->right -> color == black){
bro->color = red;//-相当于右边减去多的一个黑，达到平衡
delete_son = delete_son->parent;
}else{
//-如果是左红右黑,变成左黑右红
if (bro->right->color == black){
bro -> color = red;
bro->left->color = black;
rightRotate(bro);//-左节点上浮，相当于左右都加了一个黑，不改变平衡
}
bro->color = bro->parent -> color;
bro->parent -> color = black;
bro->right->color = black;//-给右边加了一个黑
leftRotate(delete_son->parent);//-父亲下沉，兄弟上浮，左边加一个黑，右边减一个黑，总体上左边填上了缺少的黑也达到了平衡
delete_son = root;
}
}
//-如果是右枝（不用记规则，把上面的代码left和right对调即可）
else {
RBtree_node * bro = delete_son->parent->left;
if(bro->color == red){
bro->color = black;
delete_son->parent->color = red;
rightRotate(delete_son->parent);
bro = delete_son->parent->left;
}
if(bro->right->color == black&&bro->left -> color == black){
bro->color = red;
delete_son = delete_son->parent;
}else{
if (bro->left->color == black){
bro -> color = red;
bro->right->color = black;
leftRotate(bro);
}
bro->color = bro->parent -> color;
bro->parent -> color = black;
bro->left->color = black;
rightRotate(delete_son->parent);
delete_son = root;
}
}
}
delete_son->color = black;
}

二叉树层序遍历和中序遍历

每次插入删除的时候，使用层序遍历打印一遍二叉树，可以验证一下是否正确。

每个节点都有前缀，b代表黑节点，r代表红节点。

//-层序遍历打印红黑树
void RBtree::print(){
std::deque<RBtree_node*> dqueue;//-使用deque实现队列
dqueue.push_back(root);
while(!dqueue.empty()){
int size = (int)dqueue.size();
for (int i = 0; i < size; ++i) {
RBtree_node* temp = dqueue.front();
dqueue.pop_front();
if(temp->left!=nullptr){
dqueue.push_back(temp -> left);
}
if(temp -> right != nullptr){
dqueue.push_back(temp -> right);
}
std::string color = temp->color?"b: ":"r: ";
std::string keystr = temp==nil?"nil":std::to_string(temp->key);
std::cout<<color<<keystr<<" ";
}
std::cout<<std::endl;
}
}

//-打印中序遍历
void RBtree::printMiddle(RBtree_node * node){
if(node == nil){
return;
}
printMiddle(node->left);
std::string color = node->color?"b:":"r:";
std::cout<<color<<std::to_string(node->key)<<" ";
printMiddle(node->right);
}

红黑树测试代码

写个循环来插入元素，输入i插入元素，输入d删除元素，输入q退出程序。

附上一个在线生成红黑树的连接，可以配合测试自己写的红黑树的正确性

红黑树动画在线演示

int main(){
RBtree rb;
std::string select;
KEY_TYPE key;
while(true){
std::cout<<"\n输入操作：i：插入key，d：删除key q：退出"<<std::endl;
std::cin>>select;
if(select == "i"){
std::cout<<"输入key"<<std::endl;
std::cin>>key;
rb.insertNode(key);
}else if(select == "d"){
std::cout<<"输入key"<<std::endl;
std::cin>>key;
rb.deleteNode(key);
}else if(select == "q"){
break;
}else{
std::cout<<"输入不合法，重新输入"<<std::endl;
}
}
return 0;
}

完整代码

#include <iostream>
#include <deque>
#include <string>
#include <vector>

//-既然标题是c++，那么就写成满满的c++风格吧
using Color = bool;//-颜色因为只有红或者黑，选择bool类型
using KEY_TYPE = int;//-为了更好理解红黑树，就不写成模板类了，所以首选万年int（笑~）
using VALUE_TYPE = int;//-同理

//-全局静态红黑变量
static const Color red = false;
static const Color black = true;

//-红黑树的节点特点，有color，有parent

class RBtree_node
{
public:
   Color color;
   RBtree_node *parent;
   RBtree_node *left;
   RBtree_node *right;

   KEY_TYPE key;//-后期如果想解耦合，可以将key和value抽离出去
   VALUE_TYPE value;
   RBtree_node(Color color_) :color(color_), parent(nullptr), left(nullptr), right(nullptr), key(-99999)
   {
   }
   RBtree_node(Color color_, KEY_TYPE key_, RBtree_node *nil) :
       color(color_), parent(nil), left(nil), right(nil), key(key_)
   {
   }
};

class RBtree
{
private:
   //-红黑树数据成员：其中nil的意义在于，因为红黑树的所有叶子节点都是黑色的，所以可以将所有临近末尾的节点，
   //-都连接到这一个叶子结点nil上，同理，root的parent也可以连接到nil上，形成一个dummy空节点
   RBtree_node *root;
   RBtree_node *nil;
public:
   //-以下实现了红黑树常用接口：
   //-构造函数
   RBtree()
   {
       nil = new RBtree_node(black);//-为所有叶子节点nil初始化，颜色为黑色
       root = nil;//-红黑树为空的时候，让nil作为root
   }
   //-左旋
   void leftRotate(RBtree_node *left_node);

//- 右旋
void rightRotate(RBtree_node *right_node);

//-插入key
void insertNode(KEY_TYPE key);

//-修复插入
void fixInsert(RBtree_node *node);

//-查找某个key的节点
RBtree_node *searchNode(KEY_TYPE key);

//-查找某个节点的中序后继
RBtree_node *successor(RBtree_node *node);

//-删除key
void deleteNode(KEY_TYPE key);

//-修复删除
void fixDelete(RBtree_node *node);

//-层序遍历打印红黑树
void print();

//-打印中序遍历
void printMiddle(RBtree_node *node);

};

//-左旋
void RBtree::leftRotate(RBtree_node *left_node)
{
   RBtree_node *right_node = left_node->right;
   //-右节点的左枝条接在左节点的右枝条上
   left_node->right = right_node->left;
   if (right_node->left != nil)
   {
       left_node->right->parent = left_node;
   }
   //-右节点接在左节点的父亲上
   right_node->parent = left_node->parent;
   if (left_node == root)
   {
       //-nil不会指向任何节点，但是root->parent是nil
       root = right_node;
   }
   else if (left_node == left_node->parent->left)
   {
       left_node->parent->left = right_node;
   }
   else
   {
       left_node->parent->right = right_node;
   }
   //-左节点接在右节点的左枝上
   left_node->parent = right_node;
   right_node->left = left_node;
}

//- 右旋：写完左旋后，把所有left和right对调即可
void RBtree::rightRotate(RBtree_node *right_node)
{
   RBtree_node *left_node = right_node->left;
   right_node->left = left_node->right;
   if (left_node->right != nil)
   {
       right_node->left->parent = right_node;
   }
   left_node->parent = right_node->parent;
   if (right_node == root)
   {
       root = left_node;
   }
   else if (right_node == right_node->parent->right)
   {
       right_node->parent->right = left_node;
   }
   else
   {
       right_node->parent->left = left_node;
   }
   right_node->parent = left_node;
   left_node->right = right_node;
}

//-修复插入
void RBtree::fixInsert(RBtree_node *new_node)
{
   while (new_node->parent->color == red)
   {//-终止条件要注意
//-如果父亲是左枝
       if (new_node->parent == new_node->parent->parent->left)
       {
           //-获得其伯父节点
           RBtree_node *uncle = new_node->parent->parent->right;
           if (uncle->color == red)
           {//-如果伯父是红色，那么将父亲和伯父同时变黑，不会破坏左右平衡
               uncle->color = black;
               new_node->parent->color = black;
               new_node->parent->parent->color = red;//-将祖父变红，才能实现下一轮回溯修复
               new_node = new_node->parent->parent;
           }
           else
           {//-如果伯父是黑色
       //-判断new_node是不是右孩子，如果是右孩子转换成左孩子
               if (new_node == new_node->parent->right)
               {
                   new_node = new_node->parent;
                   leftRotate(new_node);
               }
               //-此时红色节点是左孩子
               //-如果结构本是平衡状态，右边本该比左边多一个黑，但是我们将父亲（左)变黑会破坏平衡，
               //-所以需要右旋祖父，把父亲上浮，相当于在左枝多一个黑的时候给右枝也多了黑，这样左右就能平衡
               new_node->parent->color = black;
               new_node->parent->parent->color = red;
               rightRotate(new_node->parent->parent);
           }
       }
       //-如果父亲是右枝（将上边代码的left和right全部对调即可，不用记规则）
       else
       {
           RBtree_node *uncle = new_node->parent->parent->left;
           if (uncle->color == red)
           {//-如果伯父是红色
               uncle->color = black;
               new_node->parent->color = black;
               new_node->parent->parent->color = red;
               new_node = new_node->parent->parent;
           }
           else
           {//-如果伯父是黑色
               if (new_node == new_node->parent->left)
               {
                   new_node = new_node->parent;
                   rightRotate(new_node);
               }
               new_node->parent->color = black;
               new_node->parent->parent->color = red;
               leftRotate(new_node->parent->parent);
           }
       }
   }
   //-如果new_node回溯到root，此时root->parent==nil（black）打破了循环，而此时root被改变成了黑色，违反了规则1，
   //-所以最后需要强行把root fix成黑色
   root->color = black;
}

//-查找某个节点的中序后继
RBtree_node *RBtree::successor(RBtree_node *node)
{
   //-如果节点有右孩子
   if (node->right != nil)
   {
       RBtree_node *res = node->right;
       while (res->left != nil)
       {
           res = res->left;
       }
       return res;
   }
   else
   {
       while (node != root && node != node->parent->left)
       {
           node = node->parent;
       }
       return node->parent;
   }
}

//-删除key
void RBtree::deleteNode(KEY_TYPE key)
{
   //-查找key所在节点
   RBtree_node *key_node = searchNode(key);
   //-实际删除的节点
   RBtree_node *delete_node;
   //-delete_node的孩子
   RBtree_node *delete_son;
   //-如果同时有左枝或者右枝条
   if (key_node->left != nil && key_node->right != nil)
   {
       delete_node = successor(key_node);
       delete_son = delete_node->right;
   }//-如果仅有左枝或者右枝条或者左右都没有
   else
   {
       delete_node = key_node;
       if (key_node->left != nil)
       {
           delete_son = key_node->left;
       }
       else
       {
           delete_son = key_node->right;
       }
   }

   //-删除deletenode
   delete_son->parent = delete_node->parent;
   //-先判断deletenode是不是根节点
   if (delete_node == root)
   {
       root = delete_son;
   }
   else if (delete_node == delete_node->parent->left)
   {
       delete_node->parent->left = delete_son;
   }
   else
   {
       delete_node->parent->right = delete_son;
   }
   //-覆盖key_node原有数据
   key_node->key = delete_node->key;
   key_node->value = delete_node->value;

   //-如果删除节点是黑色的，需要修复delete_son,注意是孩子
   if (delete_node->color == black)
   {
       fixDelete(delete_son);
   }
   //-释放空间
   delete delete_node;
   //-打印
   print();
}

//-修复删除
void RBtree::fixDelete(RBtree_node *delete_son)
{
   //-修复的原因是因为delete_son所在的枝条的黑节点比另一个枝条少一个，所以不平衡，所以需要填上左边缺失的黑，或者减掉右边多余的黑
   //-当delete_son是黑色的一直循环
   while (delete_son != root && delete_son->color == black)
   {
       //-判断delete_son所在枝条,如果是左枝
       if (delete_son == delete_son->parent->left)
       {
           //-如果兄弟是红色的
           RBtree_node *bro = delete_son->parent->right;
           if (bro->color == red)
           {
               bro->color = black;//-兄弟变黑
               delete_son->parent->color = red;//-父亲变红
               leftRotate(delete_son->parent);//-左旋父亲，兄弟上浮，相当于左右都加了一个黑，不改变平衡状态
               bro = delete_son->parent->right;//-新的bro是原来bro的左枝，因为原bro是红的，其左右枝都是黑色的，这样保证新的兄弟是黑色的
           }
           //-此时兄弟是黑色的,判断兄弟的孩子
           //-左黑右黑（兄弟的孩子平衡了）
           if (bro->left->color == black && bro->right->color == black)
           {
               bro->color = red;//-相当于右边减去多的一个黑，达到平衡
               delete_son = delete_son->parent;
           }
           else
           {
               //-如果是左红右黑,变成左黑右红
               if (bro->right->color == black)
               {
                   bro->color = red;
                   bro->left->color = black;
                   rightRotate(bro);//-左节点上浮，相当于左右都加了一个黑，不改变平衡
               }
               bro->color = bro->parent->color;
               bro->parent->color = black;
               bro->right->color = black;//-给右边加了一个黑
               leftRotate(delete_son->parent);//-父亲下沉，兄弟上浮，左边加一个黑，右边减一个黑，总体上左边填上了缺少的黑也达到了平衡
               delete_son = root;
           }
       }
       //-如果是右枝（不用记规则，把上面的代码left和right对调即可）
       else
       {
           RBtree_node *bro = delete_son->parent->left;
           if (bro->color == red)
           {
               bro->color = black;
               delete_son->parent->color = red;
               rightRotate(delete_son->parent);
               bro = delete_son->parent->left;
           }
           if (bro->right->color == black && bro->left->color == black)
           {
               bro->color = red;
               delete_son = delete_son->parent;
           }
           else
           {
               if (bro->left->color == black)
               {
                   bro->color = red;
                   bro->right->color = black;
                   leftRotate(bro);
               }
               bro->color = bro->parent->color;
               bro->parent->color = black;
               bro->left->color = black;
               rightRotate(delete_son->parent);
               delete_son = root;
           }
       }
   }
   delete_son->color = black;
}

//-层序遍历打印红黑树
void RBtree::print()
{
   std::deque<RBtree_node *> dqueue;//-使用deque实现队列
   dqueue.push_back(root);
   while (!dqueue.empty())
   {
       int size = (int)dqueue.size();
       for (int i = 0; i < size; ++i)
       {
           RBtree_node *temp = dqueue.front();
           dqueue.pop_front();
           if (temp->left != nullptr)
           {
               dqueue.push_back(temp->left);
           }
           if (temp->right != nullptr)
           {
               dqueue.push_back(temp->right);
           }
           std::string color = temp->color ? "b: " : "r: ";
           std::string keystr = temp == nil ? "nil" : std::to_string(temp->key);
           std::cout << color << keystr << " ";
       }
       std::cout << std::endl;
   }
}

//-打印中序遍历
void RBtree::printMiddle(RBtree_node *node)
{
   if (node == nil)
   {
       return;
   }
   printMiddle(node->left);
   std::string color = node->color ? "b:" : "r:";
   std::cout << color << std::to_string(node->key) << " ";
   printMiddle(node->right);
}

int main()
{
   RBtree rb;
   std::string select;
   KEY_TYPE key;
   while (true)
   {
       std::cout << "\n输入操作：i：插入key，d：删除key q：退出" << std::endl;
       std::cin >> select;
       if (select == "i")
       {
           std::cout << "输入key" << std::endl;
           std::cin >> key;
           rb.insertNode(key);
       }
       else if (select == "d")
       {
           std::cout << "输入key" << std::endl;
           std::cin >> key;
           rb.deleteNode(key);
       }
       else if (select == "q")
       {
           break;
       }
       else
       {
           std::cout << "输入不合法，重新输入" << std::endl;
       }
   }
   return 0;
}