⏩博主CSDN主页:杭电码农-NEO⏩

⏩专栏分类:刷题分享⏪

⏩代码仓库:NEO的学习日记⏩

🌹关注我🫵带你刷更多C语言和数据结构的题!
🔝🔝

在这里插入图片描述

链式二叉树OJ题分享

1. 前言🚩
2. 单值二叉树🚩
- 2.1 审题🏁
- 2.2 代码实现🏁
3. 检查两颗树是否相同🚩
- 3.1 审题🏁
- 3.2 代码实现🏁
4. 对称二叉树🚩
- 4.1 审题🏁
- 4.2 代码实现🏁
5. 二叉树的前中后序遍历🚩
- 5.1 审题🏁
- 5.2 代码实现🏁
6. 总结🚩

1. 前言🚩

链式二叉树这一个板块的考题还是比较多的,这里我给大家分享几道很经典的OJ题,仅供参考! 分别是 1. 单值二叉树力扣965题----- 2. 检查两棵树是否相同力扣100题 ----- 3. 对称二叉树 力扣101题

2. 单值二叉树🚩

2.1 审题🏁

在这里插入图片描述

这个题很简洁,让我们判断一个二叉树所有节点的值是否相同,这里的题我们都最好用递归的思想解决,因为非递归往往比较困难.我们先从易到难.我们可以想到的思路是:

如果二叉树为空树,我们应该返回true

当前节点不为空时,我们就要用分治的思想,先判断当前节点的左孩子是不是NULL节点,如果不是空节点就将当前节点存储的值与左孩子节点存储的值进行比较右边也是如此

判断左右子树是否为空,不为空的子树就判断当前节点与子树节点存储的值是否相同

这种分治思想可以理解为我们当前节点与孩子节点的值相同后又去比较孩子节点与孩子的孩子节点是否相同,如果遇见不相同的返回false,相同就一直往下走直到遇见NULL

2.2 代码实现🏁

我们可以根据前面的两个判断写出这样的代码:

bool isUnivalTree(struct TreeNode* root)
{
    if(root==NULL)//如果树为空或当前节点为空就返回true
    {
        return true;
    }
    if(root->left!=NULL&&root->val!=root->left->val)
    {
        return false;
    }
    if(root->right!=NULL&&root->val!=root->right->val)
    {
        return false;
    }
}

这里需要注意的是,当 root==NULL时有两种情况,一是我们拿到的树本身就是一个空树,我们返回true是没有问题的,二是我们往后递归下去的某个节点是空节点,走到空节点代表这条路线上所有节点的值都一样,返回true也没问题

然而当我们走完上面代码后,既没有返回true也没有返回false,走到这里就代表此节点即不为空,并且它和它孩子的值也是相同的,所以这里我们就去到它的左右子树再次重复上面的过程

bool isUnivalTree(struct TreeNode* root)
{
    if(root==NULL)
    {
        return true;
    }
    if(root->left!=NULL&&root->val!=root->left->val)
    {
        return false;
    }
    if(root->right!=NULL&&root->val!=root->right->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);//左右子树的值都相同才返回true

}

3. 检查两颗树是否相同🚩

3.1 审题🏁

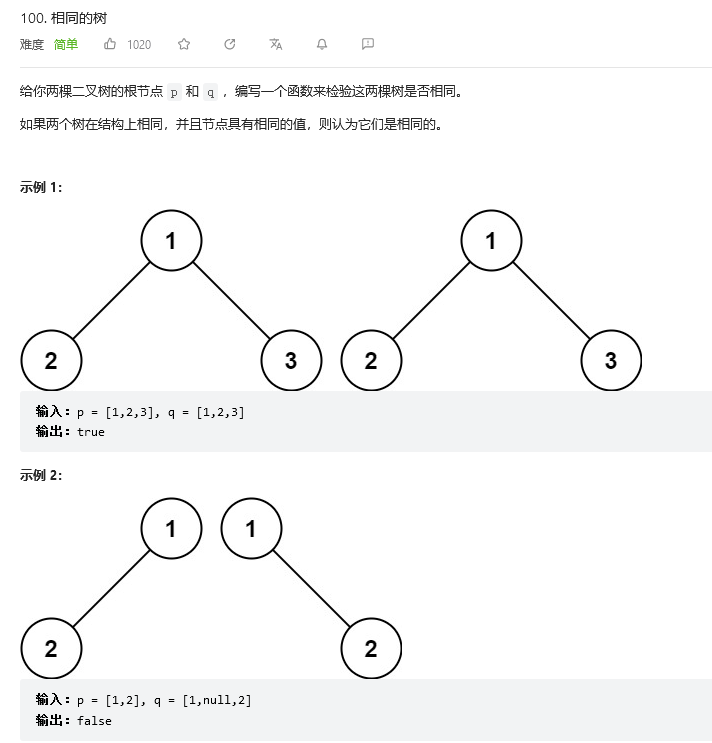
在这里插入图片描述

判断两颗树是否相同,它不仅仅是值相同,值对应的左右孩子的顺序也要相同,这里我们还是采用分治递归的思想,把大事化小,把小事化了,这里我们首先可以想到的是,当着两棵树都为空树时,它们是相同的返回true.然而这里还会出现一种情况,那就是一棵树为空,另外一颗树不为空,这时它们是不相同的,返回false.当走完上面两个条件后,说明此时这两个节点都不为空,我们就接着判断在这个节点这两棵树的值是否相同

我们可以根据上面的讨论得到这样的结论:

当两个树的节点都为空时返回true
当两个树中一个节点为空另一个节点为非空返回false
当两棵树都不为空,判断它们的值是否相同

3.2 代码实现🏁

我们根据上面的讨论可以写出这样代码:

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
}

当代码走完上面的步骤后没有返回true也没有返回false,这时说明这两个节点不为空,并且它们的值相同,这是我们就应该接着递归这两个节点的左右子树,不断重复上面的过程直到遇见不相同或为空的节点

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    bool left = isSameTree(p->left,q->left);
    bool right = isSameTree(p->right,q->right);
    if(!left||!right)//如果左子树和右子树其中一个的结果是false,那么就返回false
    {
        return false;
    }
    else
    return true;
}

这里需要注意的点是,我们递归时是将节点一的左子树和节点二的左子树放在一起递归,节点一的右子树和节点二的右子树放在一起递归.这里不能搞混淆了.并且左右子树中只要有一个false,那么就直接返回false,因为只有节点一和节点二不相同时才会返回返回false给left或right

如果左右子树都不为false,那么就代表此节点的左右子树与另外一棵树的对应节点的左右子树是相同的

4. 对称二叉树🚩

4.1 审题🏁

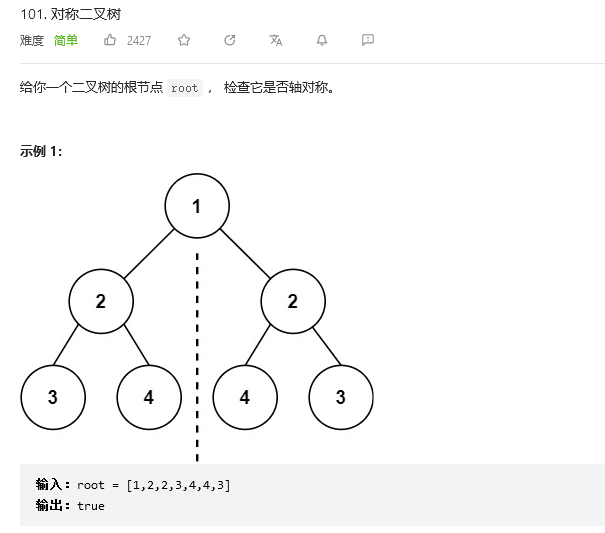
在这里插入图片描述

这个题和判断相同的二叉树很相似,上一题是左边与左边做判断,这个题要左边和右边做判断,如果是对称的二叉树的话,那么当前节点的左子树要等于当前节点的右子树,然后左子树的左子树要等于右子树的右子树,左子树的右子树要对应右子树的左子树,很绕.但是仔细一下确实是这样.我们还是用分治的思想,第一步如果当前节点的左孩子和右孩子都为空,或者说这棵树只有一层,那么它是对称的,返回true.第二步如果当前节点的左孩子或者右孩子有一个为空,一个不为空,那么这棵树就不是对称的,返回false.当我们走完上面两步还没有如何返回值时,证明左孩子和右孩子都不为空,这时就要判断左右孩子的值是否相同.

根据上面的思路总结:

左右孩子都为空,返回true
左右孩子其中一个为空另一个不为空返回false
当左右孩子都不为空时比较左右孩子对应的值是否相同

4.2 代码实现🏁

需要注意的是,这里的接口函数的参数只有一个,但是我们递归的时候想要递归左子树的左子树与右子树的右子树,我们就需要两个参数,所以我们不能在原有的接口函数上进行递归,这里我们应该自己写一个函数用来递归

bool isSymmetric(struct TreeNode* root)
{
    if(root==NULL)
    {
        return true;
    }
    struct TreeNode* left=root->left;
    struct TreeNode* right=root->right;
    return myis(left,right);
}

这里我们先把接口函数的功能给实现了,然后再来看我们的自定义函数:

bool myis(struct TreeNode* left,struct TreeNode* right)
 {
     if(left==NULL&&right==NULL)
     {
         return true;
     }
     if(left==NULL||right==NULL)
     {
         return false;
     }
     if(left->val!=right->val)
     {
         return false;
     }
}

将上面所有代码走完后,如果还是没有返回值的话,证明此时的左节点和右节点即不为空,并且它们的值相同,所以我们就接着往下递归,不断重复上面的过程

bool myis(struct TreeNode* left,struct TreeNode* right)
 {
     if(left==NULL&&right==NULL)
     {
         return true;
     }
     if(left==NULL||right==NULL)
     {
         return false;
     }
     if(left->val!=right->val)
     {
         return false;
     }
     
     return myis(left->left,right->right)&&myis(left->right,right->left);
 }

这里递归的对象是左子树的左子树和右子树的右子树是一队,而左子树的右子树和右子树的左子树是一队.并且要它们两个都返回true时,才是真正对称的,所以用&&符号连接.

5. 二叉树的前中后序遍历🚩

这里我们只需要把二叉树的前序遍历的题目给理解了,中后序自然就简单了.

5.1 审题🏁

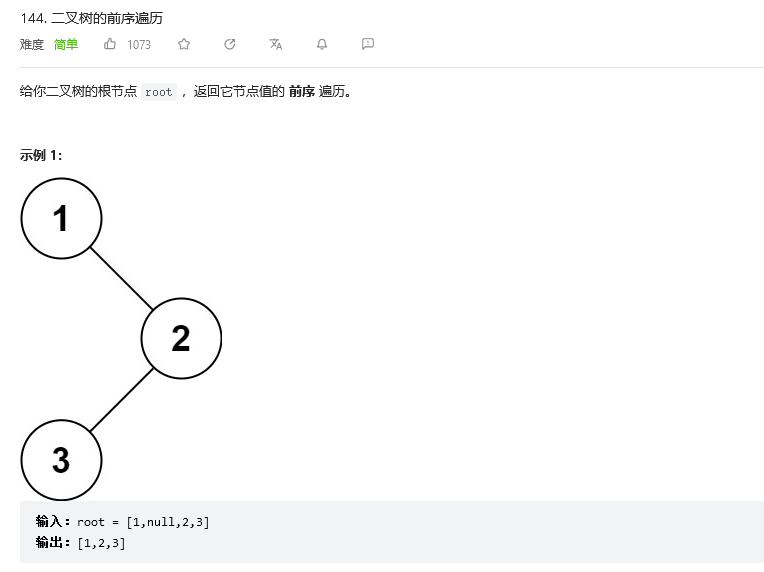
在这里插入图片描述

首先我们要先知道接口函数的参数int* returnSize.这里它实际上不是告诉我们二叉树有多少个节点的意思,而是要我们自己求出二叉树的节点个数,然后解引用returnSize修改returnSize的值,最后调用接口函数和returnsize的值判断我们的代码正不正确.所以这里我们可以自定义一个函数来求二叉树节点的个数

其次,这里要返回一个数组,数组里元素的顺序是二叉树前序遍历的顺序,所以这里我们要动态开辟一个数组.

5.2 代码实现🏁

根据上面两个思路我们可以写出这样的代码:

int TreeSize(struct TreeNode* root)//求二叉树节点个数的函数
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }
 int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    int size=TreeSize(root);
    int* a=(int*)malloc(sizeof(int)*size);
    *returnSize=size;//将二叉树节点个数赋值给returnSize

这时求二叉树节点个数的函数,如果这里你不理解这个函数是怎么实现的,可以跳转二叉树详解,或者自己画递归展开图来理解.

写到这一步后,我们想要在数组中存储元素就要定义下标,而如果直接在要递归的函数中定义下标的话,每次递归后下标都会重置为0,就相当于每次都在操作数组里的第一个元素,所以这里我们采用了一个很巧妙的方式,将定义下标的位置写在递归函数外,并且将下标的地址传进函数,这样函数不管递归多少次下标都不会出问题:

int TreeSize(struct TreeNode* root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }

 void _preorderTraversal(struct TreeNode* root,int* a,int* pi)//递归的函数
 {
     if(root==NULL)//如果节点为空就直接返回
     {
         return;
     }
     a[(*pi)++]=root->val;//前序遍历,先将节点的值给数组a,再递归左右孩子
     _preorderTraversal(root->left,a,pi);
     _preorderTraversal(root->right,a,pi);

 }
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    int size=TreeSize(root);
    int* a=(int*)malloc(sizeof(int)*size);
    int i=0;//在接口函数中定义下标
    _preorderTraversal(root,a,&i);//将下标i的地址传入要递归的函数
    *returnSize=size;
    return a;//最后返回数组a的地址

}