算法套路十八——区间 DP
- 线性DP: 具有前缀/后缀结构的问题,其中每个阶段只依赖于前一阶段的状态
- 区间DP:需要确定给定区间内所有可能状态的问题,并从较小区间向较大区间进行转移。
区间DP介绍:https://oi-wiki.org/dp/interval/
算法示例:LeetCode516. 最长回文子序列
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
法一:递归+记忆化搜索
递归定义:递归函数dfs(i,j),返回s[i:j+1]这个子串的最长回文子序列长度。
递归过程:
- 如果s[i]和s[j]相等,说明这两个字符可以成为回文子序列的一对,因此我们可以继续考虑子串s[i+1:j-1]所对应的最长回文子序列,再将长度加二。
- 如果s[i]和s[j]不相等,那么必须从s[i+1:j]和s[i:j-1]两种情况中选择一个较长的回文子序列,作为s[i:j+1]子串的回文子序列。
边界条件:- 如果已经越界(即i>j),那么返;- 如果只有一个字符(即i==j),那么返回1
返回值:返回整个输入字符串s的最长回文子序列长度,即调用dfs(0, n-1)。
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n=len(s)
@cache
def dfs(i:int,j:int):
if i>j:
return 0
if i==j:
return 1
if s[i]==s[j]:
return dfs(i+1,j-1)+2
return max(dfs(i+1,j),dfs(i,j-1))
return dfs(0,n-1)
法二:二维数组动态规划
根据递归转化为动态规划,不过本题更新dp[i][j]时,需要用到dp[i+1][j],此时dp[i+1][j]若未更新将导致结果错误;而倒序遍历,则可以保证用到的dp[i+1][j]已经是最新计算出来的值,因此我们倒序遍历i。
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n=len(s)
dp=[[0]*(n)for _ in range(n)]
for i in range(n-1,-1,-1):
dp[i][i]=1
for j in range(i+1,n):
if s[i]==s[j]:
dp[i][j]=dp[i+1][j-1]+2
else:
dp[i][j]=max(dp[i+1][j],dp[i][j-1])
return dp[0][n-1]
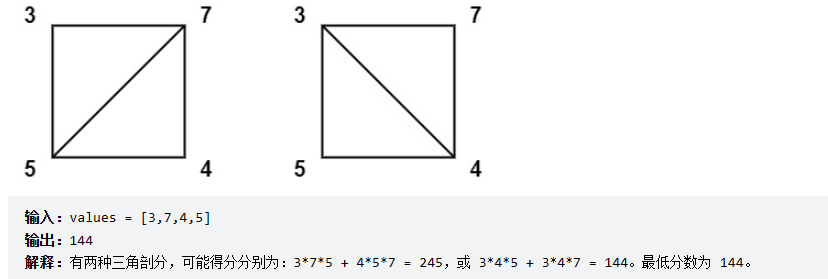
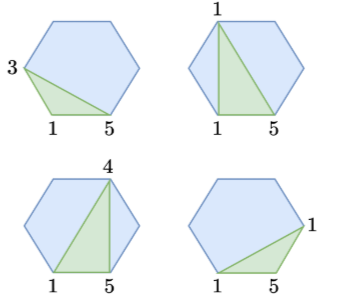
算法练习一:LeetCode1039. 多边形三角剖分的最低得分
你有一个凸的 n 边形,其每个顶点都有一个整数值。给定一个整数数组 values ,其中 values[i] 是第 i 个顶点的值(即 顺时针顺序 )。
假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形,该三角形的值是顶点标记的乘积,三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。
返回 多边形进行三角剖分后可以得到的最低分 。
法一 :递归+记忆化搜索
-
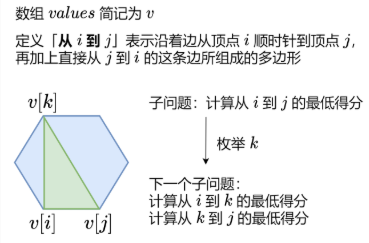
递归函数定义:dfs,接收两个参数 i 和 j 表示当前处理的顶点范围从i到j,返回值是组成最小三角剖分的分值。
-
状态转移方程:
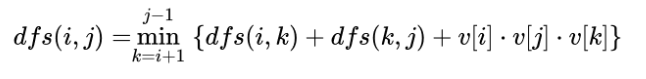
-
边界值:在递归函数中,当当前处理的顶点范围只有一个或两个点,无法组成三角形时,直接返回 0;当前顶点范围有三个点时,可以直接计算出这三个点组成的三角形的得分返回。
-
返回值:dfs(0,n-1)
class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
n=len(values)
@cache
def dfs(i:int,j:int)->int:
# 如果两个顶点之间没有其他点,则不能组成三角形,分值为0
if j-i<2:
return 0
# 如果两个顶点之间有两个其他点,则只有一种组合方式,直接计算返回分值
if j-i==2:
return values[i]*values[i+1]*values[j]
score=inf
# 第二步:枚举第k号顶点(i+1 <= k <= j-1),将第i、j号顶点和第k号顶点连边,
# 分成"第i号顶点到第k号顶点"和"第k号顶点到第j号顶点"两部分,递归求解
# 然后将两部分分值相加,并加上连接上第1号、k号和j号顶点的得分 values[i]*values[k]*values[j]
for k in range(i+1,j):
#k等于i+1时dfs(i,k)=0,k等于j-1时有dfs(k,j)=0
score=min(score,dfs(i,k)+values[i]*values[k]*values[j]+dfs(k,j))
return score
return dfs(0,n-1)
法二:动态规划
直接利用上述递归思路进行转换,不过需要注意与示例一样,dp[i][j]更新时需要dp[k][j],而k是大于i的,所以在遍历i时需要倒序遍历
func minScoreTriangulation(values []int) int {
n:=len(values)
dp:=make([][]int,n)
for i :=range dp{
dp[i]=make([]int,n)
}
// 倒序枚举左端点,且由于三角形至少3个点,故左端点从n-3开始
for i:=n-3;i>=0;i--{
// 正序枚举右端点,且由于三角形至少3个点,右端点从i+2开始枚举
for j:=i+2;j<n;j++{
dp[i][j]=math.MaxInt
// 枚举中间断点k从i+1到j-1
for k:=i+1;k<j;k++{
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+values[i] * values[j] *values[k])
}
}
}
return dp[0][n-1]
}
func min(a,b int)int{if a>b{return b};return a}
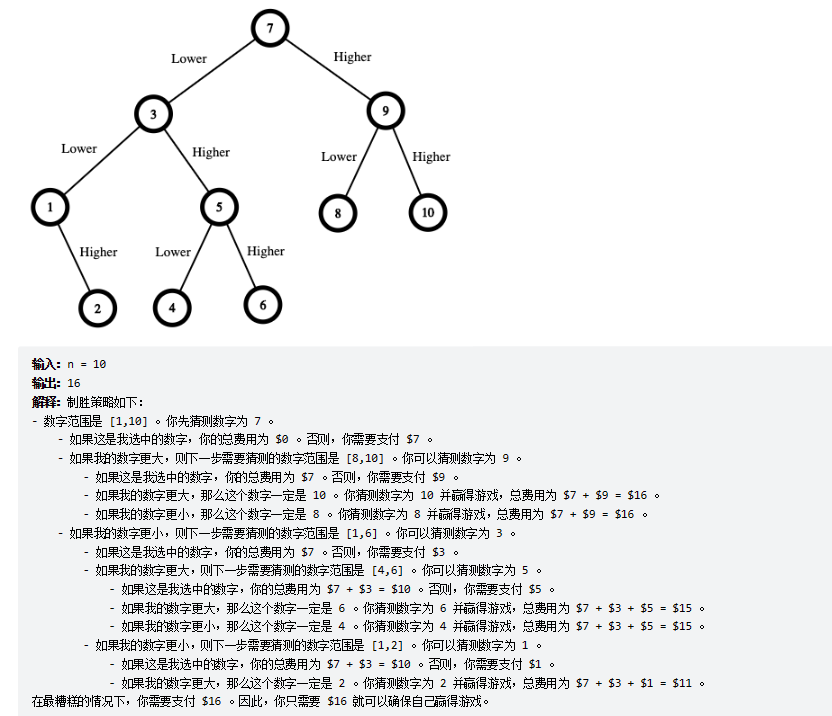
算法练习二:LeetCode375. 猜数字大小 II
我们正在玩一个猜数游戏,游戏规则如下:
我从 1 到 n 之间选择一个数字。
你来猜我选了哪个数字。
如果你猜到正确的数字,就会 赢得游戏 。
如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
每当你猜了数字 x 并且猜错了的时候,你需要支付金额为 x 的现金。如果你花光了钱,就会 输掉游戏 。
给你一个特定的数字 n ,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
法一:递归+记忆化搜索
-
递归函数定义:
dfs(i, j)表示选择在范围 [i, j] 中猜数时所需要的最小代价。 -
递归方程:由于我们要找出一个代价最小的 x 来猜测结果,因此 dp[i][j] 可以通过以下方式转移而来:在 [i,j] 的所有可能猜测数中,选出一个数 k 进行猜测,根据猜测的结果将区间 [i,j] 分成两个子区间 [i,k-1] 和 [k+1,j],求出两个区间的最大值。其中,猜测数字 k 的代价可以表示为 k,由于要最小化代价,因此我们需要枚举所有可能的 k 值,然后选取其中的最小值。可能最小的最大值有点难以理解,但是最大值是为了确保能胜利,而最小值是因为我们可以根据不同的n选择每次不同的k值即选择最佳策略,能得到最小的确保胜利的金钱。递归方程如下所示
d f s ( i , j ) = m i n ( k + m a x ( d f s ( i , k − 1 ) , d f s ( k + 1 , j ) ) ) ( i < = k < = j ) dfs(i, j) = min(k + max(dfs(i, k-1), dfs(k+1, j))) (i <= k <= j) dfs(i,j)=min(k+max(dfs(i,k−1),dfs(k+1,j)))(i<=k<=j) -
边界值:在递归函数中,当处理区间只剩下 1 个数时,猜测次数为 0,返回 0;当处理区间只剩下 2 个数时,肯定最多只需要猜一次,猜较小的那个即可,返回小的数 i;
-
返回值:dfs(1,n)返回 1 到 n 所需要的最小代价。
class Solution:
def getMoneyAmount(self, n: int) -> int:
# 缓存中间计算结果的记忆化递归函数
@cache
def dfs(i:int,j:int)->int:
# 边界情况,当 i > j 时没有可猜的数,返回 0
if i>=j:
return 0
# 边界情况,当只剩下两个数时,肯定最多只需要猜一次,猜较小的那个即可,返回小的数i
if i==j+1:
return i
# 初始化当前区间的最小代价
ans=inf
# 枚举可能的猜测数字k,计算从 [i,j] 区间猜这个数字的代价
for k in range(i,j+1):
# 递归地计算两个子问题的最大代价,并求出当前 k 猜测的代价
cost=k+max(dfs(i,k-1),dfs(k+1,j))
# 取所有可能的代价中最小的那个作为当前区间的最小代价
ans=min(ans,cost)
return ans
# 调用记忆化递归函数,返回从1到n所需要的最小代价
return dfs(1,n)
法二:动态规划
直接利用上述递归思路进行转换,不过需要注意与示例一样,dp[i][j]更新时需要dp[k+1][j],而k是大于i的,所以在遍历i时需要倒序遍历
func getMoneyAmount(n int) int {
dp:=make([][]int,n+2) // 初始化动态规划数组dp
for i:=range dp{
dp[i]=make([]int ,n+2)
}
for i:=n;i>0;i--{ // 倒序枚举i
for j:=i+1;j<=n;j++{
dp[i][j]=math.MaxInt // 初始化dp[i][j]为正无穷大
for k:=i;k<=j;k++{ // 枚举[i,j]区间内的数k
dp[i][j]=min(dp[i][j],k+max(dp[i][k-1],dp[k+1][j])
}
}
}
return dp[1][n]
}
func min(a,b int)int{if a>b{return b};return a}
func max(a,b int)int{if a>b{return a};return b}
算法练习三:LeetCode1312. 让字符串成为回文串的最少插入次数
给你一个字符串 s ,每一次操作你都可以在字符串的任意位置插入任意字符。
请你返回让 s 成为回文串的 最少操作次数 。「回文串」是正读和反读都相同的字符串。
法一:递归+记忆化搜索
递归函数定义:dfs(i,j),其中i 和 j 表示当前递归处理的子串的左右两端的索引位置。
状态转移方程:分为两种情况。若当前子串两端字符相同,则需要插入次数与去掉两端后的子串相同。若当前子串两端字符不相同,则可以讨论在左端或右端插入一个字符,使得当前子串变成回文串。因此需要递归处理两种情况并取最小值。
边界值:当子串为空或只有一个字符时不需要插入;当子串只有两个字符时,若两端字符相等则不需要插入,否则需要插入一次。
返回值:dfs(0,n-1)
class Solution:
def minInsertions(self, s: str) -> int:
n=len(s)
@cache
def dfs(i:int,j:int)->int:
if i >= j: # 当子串为空或只有一个字符时不需要插入
return 0
if i + 1 == j: # 当子串只有两个字符时
if s[i] == s[j]: # 对称则不需要插入
return 0
else: # 不对称需要插入一次
return 1
if s[i] == s[j]: # 当子串两端字符相同,则递归处理去掉两端后的子串
return dfs(i + 1, j - 1)
else: # 当子串两端不相同时,则用两种方式插入一次字符,取最小值
return 1 + min(dfs(i, j - 1), dfs(i + 1, j))
return dfs(0,n-1)
法二:动态规划
直接利用上述递归思路进行转换,不过需要注意与示例一样,dp[i][j]更新时需要dp[k+1][j],而k是大于i的,所以在遍历i时需要倒序遍历
func minInsertions(s string) int {
n:=len(s)
dp:=make([][]int,n+1)
for i:=0;i<n;i++{
dp[i]=make([]int,n+1)
}
// 自底向上计算dp数组
for i:=n-1;i>=0;i--{
dp[i][i]=0 // 只有一个字符时不需要插入
for j:=i+1;j<n;j++{
dp[i][j]=math.MaxInt // 初始化为最大值
if s[i] == s[j]{
dp[i][j]=dp[i+1][j-1] // 当两端字符相同时,去掉两端后的子串已经是回文串
}else{
dp[i][j]=1+min(dp[i][j-1],dp[i+1][j]) // 分别插入左右使得两端相同,取最小值
}
}
}
return dp[0][n-1]
func min(a,b int)int{if a>b{return b};return a}
算法进阶一:LeetCode1547. 切棍子的最小成本
给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
法一:递归+记忆化搜索,不排序cuts直接遍历长度n
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
# 定义递归函数,i和j表示当前区间的左右端点
@cache
def dfs(i:int,j:int)->int:
# 边界条件:当区间长度小于等于1时,不需要再切割,返回0
if i+1>=j:
return 0
res = inf
# 枚举所有可能的切割点
for cut in cuts:
if i < cut < j:
# 递归计算左右两个子区间的最小代价,并更新最小值
res = min(res, dfs(i, cut) + dfs(cut, j) )
# 返回当前区间的最小代价,加上当前区间的长度
return res + j - i if res != inf else 0
# 调用递归函数,计算整个区间[0,n]的最小代价
return dfs(0,n)
法二:递归+记忆化搜索,排序遍历cuts
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
cuts = [0] + sorted(cuts) + [n]
@cache
def dfs(i, j): # (i, j)
if i + 1 >= j:
return 0
res = inf
for k in range(i + 1, j):
res = min(res, dfs(i, k) + dfs(k, j) + cuts[j] - cuts[i])
return res
return dfs(0, len(cuts) - 1)
法三:动态规划,排序遍历cuts
不知道为什么对于法一换为动态规划后有错误,只能对于法二进行动态规划转换
func minCost(n int, cuts []int) int {
m := len(cuts)
sort.Ints(cuts)
cuts = append([]int{0}, cuts...)
cuts = append(cuts, n)
f := make([][]int, m+2)
//[i][j] 表示在当前待切的木棍左端点为 cuts[i-1],右端点为 cuts[j+1] 时,将木棍全部切开的最小成本
for i := range f {
f[i] = make([]int, m+2)
}
for i := m; i >= 1; i-- {
for j := i; j <= m; j++ {
// 初始化 f[i][j] 的值为最大整数
f[i][j] = math.MaxInt32
// 枚举所有可能的切割点 k
for k := i; k <= j; k++ {
// 更新 f[i][j] 的值为左右两个子区间的最小代价加上当前区间的代价
f[i][j] = min(f[i][j], f[i][k-1]+f[k+1][j])
}
f[i][j] += cuts[j+1] - cuts[i-1]
}
}
return f[1][m]
}
func min(a,b int)int{if a>b{return b};return a}
算法练习五:LeetCode1000. 合并石头的最低成本
有 N 堆石头排成一排,第 i 堆中有 stones[i] 块石头。
每次移动(move)需要将连续的 K 堆石头合并为一堆,而这个移动的成本为这 K 堆石头的总数。
找出把所有石头合并成一堆的最低成本。如果不可能,返回 -1 。

法一:递归+记忆化搜索
本题有一定的难度,首先对于数组nums想要求nums[i:j]的和,我们要想到使用前缀和,定义它的前缀和 s [ 0 ] = 0 , s [ i + 1 ] = ∑ j = 0 i stones [ j ] \textit{s}[0]=0,\textit{s}[i+1] = \sum\limits_{j=0}^{i}\textit{stones}[j] s[0]=0,s[i+1]=j=0∑istones[j]
通过前缀和,我们可以把子数组的元素和转换成两个前缀和的差,即
∑ j = left right stones [ j ] = ∑ j = 0 right stones [ j ] − ∑ j = 0 left − 1 stones [ j ] = s [ right + 1 ] − s [ left ] \sum_{j=\textit{left}}^{\textit{right}}\textit{stones}[j] = \sum\limits_{j=0}^{\textit{right}}\textit{stones}[j] - \sum\limits_{j=0}^{\textit{left}-1}\textit{stones}[j] = \textit{s}[\textit{right}+1] - \textit{s}[\textit{left}] j=left∑rightstones[j]=j=0∑rightstones[j]−j=0∑left−1stones[j]=s[right+1]−s[left]
其次,也要考虑能否将数组合并成1堆,由于每次都会合并K堆为1堆,即每次减少k-1堆,原本n堆,最后剩余1堆,故可以通过判断n-1能否整除k-1判断是否能够为合并为1堆。
class Solution:
def mergeStones(self, stones: List[int], k: int) -> int:
n = len(stones)
# 每次减少k-1堆,最后剩一堆,如果无法整除说明无法合并成一堆
if (n - 1) % (k - 1):
return -1
s = list(accumulate(stones, initial=0)) # 前缀和
@cache # 缓存装饰器,避免重复计算 dfs 的结果
def dfs(i: int, j: int) -> int:
if i == j: # 只有一堆石头,无需合并
return 0
#m每次增加k-1,故每次dfs(i, m)与dfs(m + 1, j)都可以合并成一堆
res = min(dfs(i, m) + dfs(m + 1, j) for m in range(i, j, k - 1))
# 如果j-i是k-1的倍数,则一定可以合并成一堆
# 说明从i到j所有元素都要移动,故加上从i到j的所有前缀和
#如果j-i不是k-1的倍数,则说明当前不能合并为一堆,故不能将从i到j所有合并,需要留到后续添加
if (j - i) % (k - 1) == 0:
res += s[j + 1] - s[i]
return res
return dfs(0, n - 1)
可能不太容易理解,就拿示例举例,dfs(0,4)首先m为i即m=0,故可分为dfs(0,0)+dfs(1,4),而dfs(1,4)可以分为dfs(1,1)+dfs(2,4)或者dfs(1,3)+dfs(4,4),其中最小的是dfs(1,3)+dfs(4,4)=8+0=8。此时回到dfs(0,4)中的res=dfs(0,0)+dfs(1,4)=0+8=8,之后由于 (j - i) % (k - 1) = 0,故说明能合并成一堆,从i到j所有的石头都会移动,故 res += s[5] - s[0]=8+17=25.
法二:动态规划
同理根据递归代码修改为二维数组DP,i倒序遍历
func mergeStones(stones []int, k int) int {
n := len(stones)
if (n-1)%(k-1) > 0 { // 无法合并成一堆
return -1
}
//前缀和数组s
s := make([]int, n+1)
for i, x := range stones {
s[i+1] = s[i] + x
}
dp := make([][]int, n)
for i := n - 1; i >= 0; i-- {
dp[i] = make([]int, n)
for j := i + 1; j < n; j++ {
dp[i][j] = math.MaxInt
for m := i; m < j; m += k - 1 {
dp[i][j] = min(dp[i][j], dp[i][m]+dp[m+1][j])
}
if (j-i)%(k-1) == 0 { // 可以合并成一堆
dp[i][j] += s[j+1] - s[i]
}
}
}
return dp[0][n-1]
}
func min(a, b int) int { if b < a { return b }; return a }