熵编码基本原理
消息与信息
把客观物质运动和主观思维的活动状态表达出来就成为了消息;消息中包含信息,是信息的载体;因此,信息与消息既有区别又有联系的;
获取信息的过程就是一个消除或部分消除不确定性的过程;
信息是事物运动状态或存在方式的不确定性的描述;
信息的多少我们成为信息量;信息量与不确定性消除的程度有,消除的不确定性大 , 信息量就大; 反之,信息量就小;
自信息是信源发出某一符号所含有的信息量,信源发出的符号不同, 含有的信息量不同;
熵
自信息的数学期望为信源的信息熵;
信息熵是从平均意义上表示信源的, 总体信息测度,可以理解为信源 X 每输出一个符号所提供的平均信息量;
熵的取值总是非负数;
变长编码
对信源输出的消息 (一个信源符号或者固定数目的多个信源符号) 采用不同长度的码字表示,这种编码方式称为变长编码。
为了提高编码效率,需要根据符号出现的概 率大小设计码长,即对于大概率符号采用较短的码字表示 ,小概率符号采用较长的码字表示,以达到平均码长最短的目的;
变长码必须是唯一可译码,才能实现无失真编码;
哈夫曼编码是一种最佳变长码;但存储空间要求大、解码复杂度高;
指数哥伦布码(Exponential Golomb Code)是弥补哈夫曼的不规则结构的解码复杂度,应用最广泛的;
算术编码
与变长码不同,算术编码的本质是为整个输入序列分配一个码字, 而不是给每个输入流中的每个字符分别指定码字, 因此平均意义上可以为单个字符分配码长小于1 的码字,所以算术编码可以给出接近最优的编码结果;
算术编码的基本原理
根据信源可能发生的不同符号序列的概 率, 把 [0, 1) 区间划分为互不重叠的子区间,子区间的宽度恰好是各符号序列的概率 , 这样信源发出的不同符号序列将与各子区间一一对应。因此每个子区间内的任意一个实数都可以用来表示对应的符号序列 , 这个数就是该符号序列所对应的码字。显然,一串符号序列发生的概率越大,对应的子区间就越宽,要表达它所用的比特数就越少,因而相应的码字就越短。
算术编码的两个基本参数:符号的概率和它的编码间隔;信源符号概率决定编码过程中信源符号的间隔,而这些间隔包含在0到1之间,编码过程中的间隔决定了符号压缩后的输出。
零阶指数哥伦布编码
● 零阶指数哥伦布码是指数哥伦布码家族中的一员,它可以直接根据公式解析码字,无须查表,解码复杂度较低;
● 在h265中被用于视频参数集VPS、序列参数集SPS、图像参数集PPS、片头信息等所设计的大部分语法元素中;
● 主要分为无符号数的指数哥伦布编码ue(v)、有符号书的指数哥伦布编码se(v);
CABAC
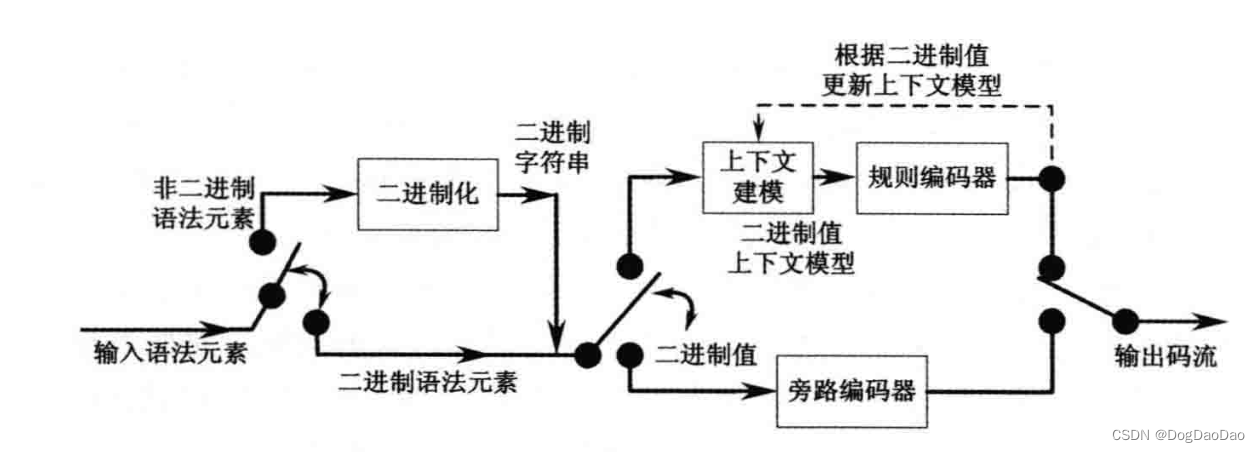
基于上下文的自适应二进制算术编码是一种将自适应的二进制算术编码与一个设计精良的上下文模型结合起来的方法;
采用了算术编码思想,同时充分考虑了视频流相关统计特性,提高了编码效率;
基本步骤:二进制化、上下文建模、二进制算术编码;
霍夫曼二元化效率高,但复杂度高,一般都采用一元码、定长码、指数哥伦布码的二元方法;h265中采用的是截断莱斯二元化TR、K阶指数哥伦布二元化EGK、定长二元化FL;不同的语法元素采用不同的二元化方法;
根据条件熵理论,利用其他己编码的语法元素进行条件编码 ,相对于独立编码或者无记忆编码能够进一步提高编码性能,这些用来作为条件的己编码符号信息称为上下文;
在h265中采用查表的方式来为每种语法元素进行上下文模型参数初始化;
二进制算术编码对当前语法元素二进制化后的每一个Bin根据其概率模型参数进行算术编码,得到最后的输出码流;
变换系数熵编码
量化后变换系数的熵编码在整个熵编码中占有举足轻重地位,量化后变化系数大多为零值或幅度较小的值;
通过编码非零系数的位置信息和非零系数的幅值来表示变换系数;
● 变换系数的扫描
○ 基于4x4大小的子块进行,较大的TB都需要进行分割成多个4x4子块;
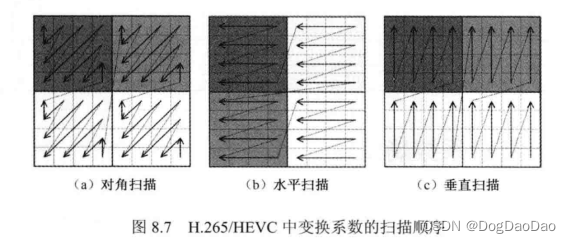
○ h265中扫描方式:对角扫描(类似h264中的zig-zag)、水平扫描、垂直扫描;
○ h265中扫描方式与预测模式存在对应关系,如4x4和8x8TB帧内预测,垂直预测模式对应水平扫描方式;16x16、32x32TB的帧内以及帧间预测模式采用对角扫描;
h265标准对变换后的非零系数位置信息和幅值信息进行CABAC编码。
符号数据隐藏技术SDH
参考:https://blog.csdn.net/Dillon2015/article/details/104254432
为什么用SDH
因为每个非零系数符号语法元素采用coeff_sign_flag来标识,用来表示该系数是正值还是负值,通过旁路编码器进行熵编码,可以加快整个编码以及解码的速度,该标识在视频压缩码流里占据很大比例,大约15%~20%;
为了减少其比特数,H265中对非零系数符号允许使用符号数据隐藏技术(Sign Data Hiding,SDH);
变换系数扫描方式
H.265/HEVC对变换系数的扫描是基于4x4块的,所以对于大于4x4的TB要先将其分为若干个4x4的子块,子块内部和子块间按同样方式进行扫描。
CG
每个4x4子块扫描后得到的16个连续的系数称为系数组(Coefficient Group,CG)。
原理:
首先计算CG内所有非零系数绝对值之和,若和为偶数则CG内最后一个非零系数被判定为“+”;若和为奇数则CG内最后一个非零系数被判定为“-”;使用SDH后解码端可以直接判断CG中最后一个非零系数的符号,编码端可以省略它的语法元素coeff_sign_flag的熵编码。
当SDH得到的符号和CG内最后一个非零系数符号不一致时就需要调整CG中某个非零系数,将它的值加1或减1,以使其和真实符号一致。所以使用SDH技术可能会带来变换系数的失真,但符号位在熵编码时使用的是旁路编码模式开销较大,使用SDH技术节约的码率大于一个变换系数失真带来的影响。
后果
视频编码中除了量化会引入失真,SDH也会。