一. 下一个更大元素

1. 下一个更大元素 Ⅰ

添加链接描述
在这里插入图片描述

2. 下一个较大元素II

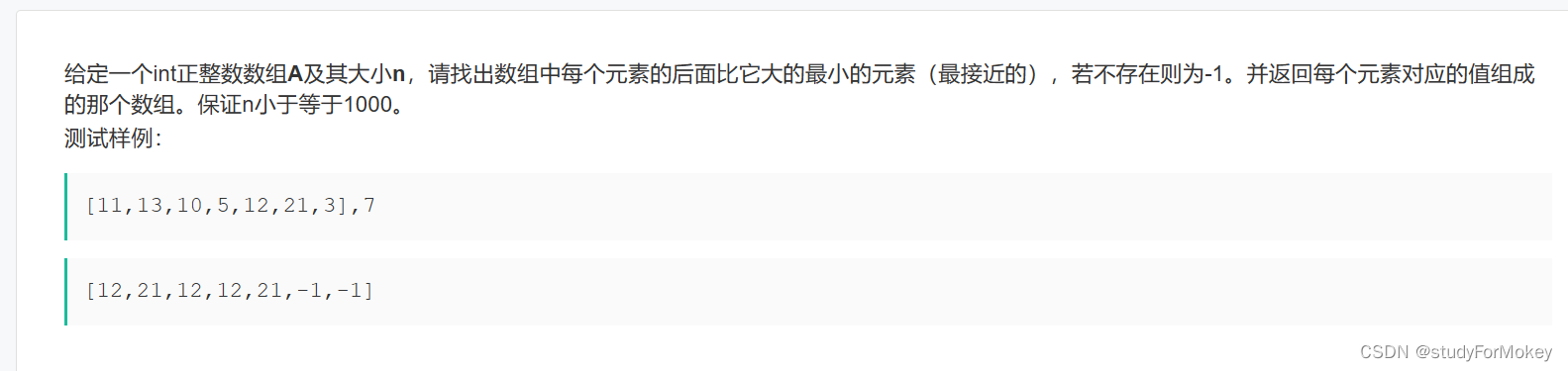
在这里插入图片描述
添加链接描述

思路分析
维护单调递减的主栈(用来取结果,题目要求最小，因此是单调递减)和单调递增(跟主栈反过来)的辅助栈
题目要求的是在当前元素后面比它大，且是最小的那个元素，因此相当于后边的元素要一直用，且排好序，因此想到用一个栈接住弹出的元素，再将其添加到原来的栈中
为了处理后边的元素排序，因此需要从后边开始遍历
当主栈不满足单调递减时，弹出元素，且用辅助栈保存结果

import java.util.*;

public class NextElement {
    public int[] findNext(int[] A, int n) {
        int[] res = new int[n];
        Stack<Integer> stack = new Stack<>();//主栈
        Stack<Integer> stack2 = new Stack<>();//辅助栈
        for (int i = n - 1; i >= 0; i--) {
            while (!stack.isEmpty() && stack.peek() <= A[i]) {//保证单调递减
                stack2.push(stack.pop());//用辅助栈保留结果,
            }
            res[i] = stack.isEmpty() ? -1 : stack.peek();//单调递减的栈顶元素为所求
            stack.push(A[i]);//入栈
            while (!stack2.isEmpty()) {//其余元素也需要回到栈
                stack.push(stack2.pop());
            }
        }
        return res;
    }
}

二. 区间问题

1. 贪心策略

最少射箭问题

板子题,排序后，比较后一个元素的左边界和前一个元素的右边界，无重叠+1，出现重叠就更新右边界

无重叠区间

前一题的变形，反过来求结果，区别在于边界相等时的处理不一样

合并区间

前几题的变形，left和right记录最新边界

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals,(a,b)->(a[0]-b[0]));
        int left = intervals[0][0];
        int right = intervals[0][1];
        LinkedList<int[]> res = new LinkedList<>();
        for(int i=1;i<intervals.length;i++){
            if(intervals[i][0]>intervals[i-1][1]){
                res.add(new int[]{left,right});
                left = intervals[i][0];
                right = intervals[i][1];
            }else{
                intervals[i][1] = Math.max(intervals[i][1],intervals[i-1][1]);
                right = Math.max(intervals[i][1],intervals[i-1][1]);
            }
        }
        res.add(new int[]{left,right});
        return res.toArray(new int[res.size()][2]);
    }
}