目录
瑞典生育率现状与影响因素分析
一、研究目的
二、数据来源和相关说明
三、描述性分析
3.1 样本描述
3.2 数据可视化
四、数学建模
4.1 模型建立
4.2 模型结果
(1)全模型A
(2)全模型B
(3)全模型A、B比较
(4)逐步回归模型
4.3 模型诊断
4.4 模型预测
五、结论及建议
5.1 结论
5.2 建议
六、R语言代码
瑞典生育率现状与影响因素分析
摘要:通过对swiss数据集的分析,本文得出了如下结论。首先,目前瑞典生育率平均水平为70.14(平均值),各城市生育率大致服从正态分布,主要集中在60-80之间。其次,以对数生育率为因变量建立全回归模型效果更好,其中农业、教育、天主教徒和婴儿死亡率对生育率有显著影响。婴儿死亡率对生育率的正向影响最大,教育对生育率的负向影响最大。第三,建立逐步回归模型对全模型进行选择时,剔除了变量Examination。逐步回归模型通过了自变量共线性检验和模型诊断,模型拟合效果好。以80%样本进行拟合,20%样本进行预测时,均方根误差为0.089,模型预测效果非常好。可以考虑为高教育水平人群提供更多生育福利,适当减缓国民经济负担,增强天主教的宣传,进而提高生育率。
一、研究目的
生育率(Fertility Rate)是指不同时期、不同地区妇女或育龄妇女的实际生育水平或生育子女的数量。生育率是一个重要指标,随着时间推移,尤其是21世纪以来,世界各国的生育率都存在大幅度下降。若放任不管,人口负增长现象便会出现或加重,就会形成严峻的人口问题。生育的问题一定要提前发现,提早解决。生育率受生物因素、文化因素、政治因素、经济因素等多方面影响。
1888年,瑞士进入了人口转型时期,也就是说,它的生育率开始从不发达国家的典型高水平下降。本文欲基于R语言分析faraway包中swiss数据集,对瑞典的生育率情况与生育率影响因素进行探究与分析。
二、数据来源和相关说明
本文数据来源于R语言分析faraway包中的swiss数据集。Swiss数据集是1888年瑞典生育率和社会经济指标数据,反映了瑞士47个说法语的省份标准化生育率和社会经济状况。数据集维度为47*6,包含了生育率和五个社会经济指标数据,这些数据全为连续型变量,数据具体情况如表2-1所示。
表2-1 变量及其含义
| 变量 | 含义 | 符号 |
| Fertility | 标准化生育率 | Y |
| Ln(Fertility) | 对数生育率 | Ln(Y) |
| Agricultre | 以农业为职业的男性百分比 | X1 |
| Examination | 在军队考试中获得最高分的应征者 | X2 |
| Education | 应征入伍者中进行小学以上教育 | X3 |
| Catholic | 天主教徒(与“新教徒”相对) | X4 |
| Infant.Mortality | 婴儿死亡率 | X5 |
三、描述性分析
为了获得对数据的整体了解,本文首先对数据进行了描述性统计分析。
3.1 样本描述
表3-1 样本描述
| 变量 | Min | Max | Median | Mean |
| Fertility | 35.00 | 92.50 | 70.40 | 70.14 |
| Ln(Fertility) | 3.56 | 4.53 | 4.25 | 4.23 |
| Agricultre | 1.20 | 89.70 | 54.10 | 50.66 |
| Examination | 3.00 | 37.00 | 16.00 | 16.49 |
| Education | 1.00 | 53.00 | 8.00 | 10.98 |
| Catholic | 2.15 | 100.00 | 15.14 | 41.14 |
| Infant.Mortality | 10.80 | 26.60 | 20.00 | 19.94 |
由表3-1可以得出:生育率介于35.00-92.50之间,其平均水平约为70.14(平均值)和70.40(中位数);对数生育率介于3.56-4.53之间,其平均水平约为4.23(平均值)和4.25(中位数);农业水平介于1.20-89.70之间,其平均水平为50.66(平均值)和54.10(中位数);审查水平介于3.00-37.00之间,其平均水平为16.49(平均值)和16.00(中位数);教育水平介于1.00-53.00之间,其平均水平为10.98(平均值)和8.00(中位数);天主教徒介于2.15-100.00之间,其平均水平为41.14(平均值)和15.14(中位数);婴儿死亡率介于10.80-26.60之间,其平均水平为19.94(平均值)和20.00(中位数)。
3.2 数据可视化
为了更直观地看数据的分布情况以及变量与变量间的线性相关情况,本文用R软件,分别绘制了6个变量的直方图和相关性热力图,同时对本文研究对象“生育率”取了对数,绘制了“对数生育率”直方图,图形如图3-1-图3-3所示。
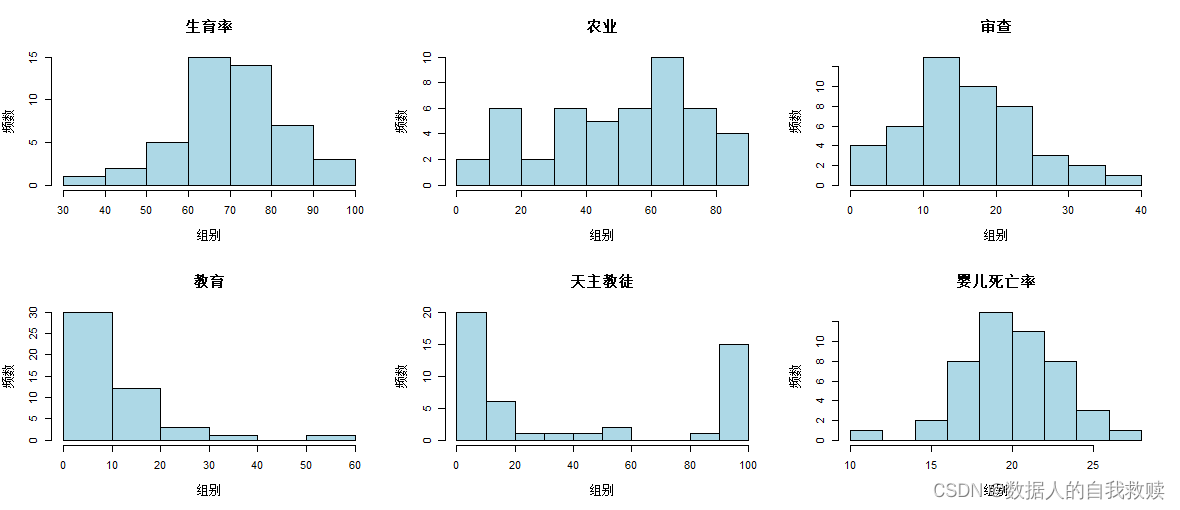
图3-1 变量直方图
由图3-1可以得出:生育率大致服从正态分布,主要集中在60-80之间,其中60-70频率最高;农业水平分布不规律,整体上看分布较为均匀,60-70频率最高,0-10和20-30频率最低,其他组频率大致相同;审查水平也大致服从正态分布,主要集中咋10-25之间,其中10-15频率最高;教育水平大致服从指数分布,主要集中在0-20之间,其中0-10频率最高;天主教徒的分布呈现“两端高,中间低”的特点,主要集中在0-20与90-100之间,其中0-10频率最高;婴儿死亡率大致服从指数分布,主要集中在16-24之间,其中18-20频率最高。
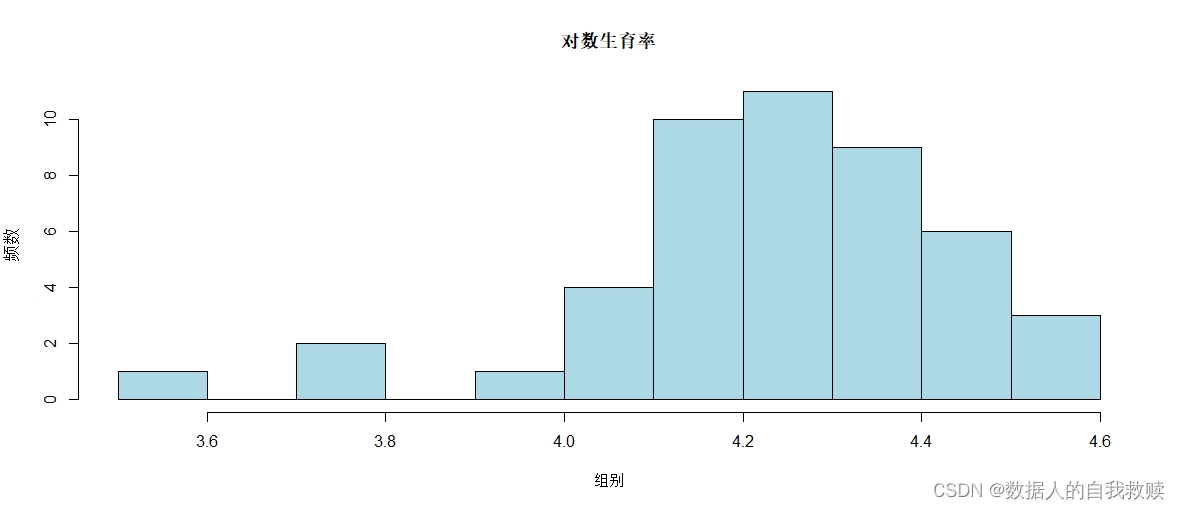
图3-2 对数生育率直方图
由图3-2可以得出:与生育率相比,对数生育率呈现“断区间”分布状态,即对数生育率整体分布在3.5-4.6之间,但是在区间3.6-3.7以及3.8-3.9之间不存在数据。整体上看,对数生育率呈现“左偏态”分布,数据主要集中在4.1-4.5,其中4.2-4.3频率最高。

图3-3 变量相关性热力图
由图3-3可以得出:7个变量中不少变量之间都存在中等或较强的正(负)相关,如Education和Examination之间相关系数为0.7,正相关性较强;如Examination和Agriculture之间相关系数为-0.69,负相关性较强。Fertility与对数Fertility和其他五个变量之间都存在中等或较强的正(负)相关,这为后续建模提供了理论依据;Infant.Mortality与除Fertility外的四个变量的线性相关性都较弱。
四、数学建模
4.1 模型建立
为了得到生育率的影响因素,本文建立了全模型A,即以Fertility为因变量,其他五个变量为自变量建立回归模型,模型表达式如下:
Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5+ε
全模型A的参数估计和模型检验结果如表4-1所示。
其次,为了探究因变量的转换对模型拟合效果的影响,本文又以对数Fertility作为因变量,其他五个变量作为自变量建立全回归模型B,模型表达式如下:
ln(Y)=β0+β1X1+β2X2+β3X3+β4X4+β5X5+ε
全模型B的参数估计和模型检验结果如也如表4-1所示。
第三,为了对自变量进行选择得到最佳模型,本文又建立了逐步回归模型,对5个自变量进行选择。从全模型A和B中选择一个拟合效果好的模型进行自变量选择,逐步回归模型参数估计结果和模型检验也如表4-1所示。
最后,对后两个模型的差异性进行检验。
4.2 模型结果
表4-1 模型参数估计
| 变量 | 全模型A | 全模型B | 逐步回归模型 | |||
| term | estimate | p.value | estimate | p.value | estimate | p.value |
| (Intercept) | 66.915 | <0.001*** | 4.184 | <0.001*** | 4.136 | <0.001*** |
| Agriculture(X1) | -0.172 | 0.019* | -0.002 | 0.024* | -0.002 | 0.029* |
| Examination(X2 ) | -0.258 | 0.32 | -0.003 | 0.50 | —— | —— |
| Education(X3 ) | -0.871 | <0.001*** | -0.016 | <0.001*** | -0.017 | <0.001*** |
| Catholic(X4 ) | 0.104 | 0.005** | 0.001 | 0.014* | 0.002 | <0.001*** |
| Infant.Mortality(X5 ) | 1.077 | 0.007** | 0.017 | 0.005** | 0.017 | 0.005** |
| Multiple R-squared | 0.707 | 0.736 | 0.733 | |||
| Adjusted R-squared | 0.671 | 0.704 | 0.7076 | |||
| p-value | <0.001 | <0.001 | <0.001 | |||
| 两模型方差分析P值 | —— | 0.505 | ||||
由表4-1可以得出:
(1)全模型A
全模型Ap值<0.001,即模型非常显著,根据参数估计值得到全模型A表达式为:
Y=66.915-0.172X1-0.258X2-0.871X3+0.104X4+1.077X5
从中可以看出,五个变量中,在显著性水平α=0.05 时,只有变量X2 不显著,即Examination不显著,其余变量都显著;变量X5 的变化对Y 的影响最大,当婴儿死亡率增加一个单位,生育率会增加1.077个单位;变量X3 对生育率的负向影响最大,当Education每增加一个单位,生育率会下降0.871;变量X4 、X5 对生育率有正向影响,而其余三个变量对生育率有负面影响。
(2)全模型B
全模型Bp值<0.001,即模型也非常显著,根据参数估计值得到全模型B表达式为:
Ln(Y)=4.184-0.002X1-0.003X2-0.016X3+0.001X4+0.017X5
从中可以看出,五个变量中,在显著性水平α=0.05 时,只有变量X2 不显著,即Examination不显著,其余变量都显著;变量X5 的变化对Ln(Y) 的影响最大,当婴儿死亡率增加一个单位,对数生育率会增加为原来的1.017倍;变量X3 对对数生育率的负向影响最大,当Education每增加一个单位,对数生育率会下降为原来的0.984倍;变量X4 、X5 对对数生育率有正向影响,而其余三个变量对生育率有负面影响。
(3)全模型A、B比较
由两个模型的P值可以看出,两个模型均高度显著;根据R2 和调整的R2 可以看出,全模型B的值略大,即拟合效果略好。因而,文本选择全模型B进行进一步分析与预测。
(4)逐步回归模型
逐步回归模型剔除了全模型B中不显著的变量X2 ,保留了其余四个自变量;在显著性水平α=0.05 时,变量均显著;逐步回归模型P值<0.001,逐步回归模型表达式为:
Ln(Y)=4.136-0.002X1-0.017X3+0.002X4+0.017X5
从中可以看出,逐步回归模型参数估计结果与全模型类似。由全模型B与逐步回归模型的差异性检验结果可知,两个模型之间并不存在显著性差异。考虑到全模型存在不显著的变量,因而文本选择逐步回归模型进行进一步分析。
4.3 模型诊断
首先,对逐步回归模型的自变量进行共线性诊断,结果如表4-2所示。变量X1 、X3 、X4 、X5 的VIF值均小于4,因而变量之间不存在多重共线性。
表4-2 共线性检验
| 变量 | Agriculture | Education | Catholic | Infant.Mortality |
| VIF值 | 2.147153 | 1.816361 | 1.299916 | 1.107528 |
其次,对逐步回归模型的正态性、方差齐性与异常值进行诊断,结果如图4-1所示。由左上角图形可以得出,残差基本保持水平,与估计值无关;由右上角图可以看出,点大致分布在一条直线上,即残差项基本服从正态分布;由左下角图形可以看出,方差基本保持水平,即满足等方差的假设;由右下角的图形可以看出,所有点的cook距离均小于0.5,即无异常值点。
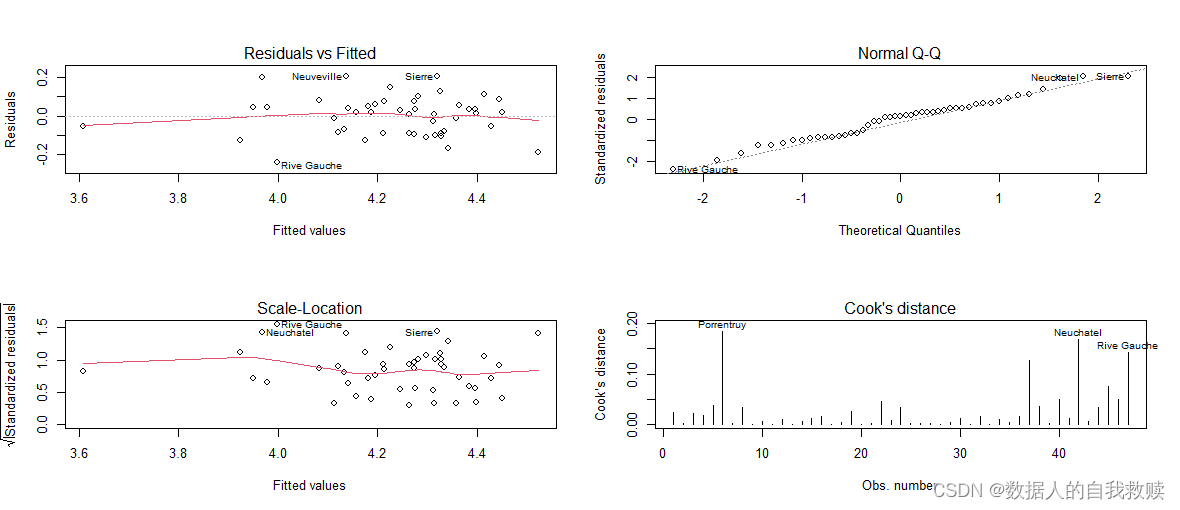
图4-1 逐步回归模型诊断
综上所述,逐步回归模型B通过了共线性检验与模型诊断。
4.4 模型预测
将swiss数据集顺序打乱,以80%作为训练集训练逐步回归模型,以20%作为测试集,对模型预测效果进行评估,训练集样本真实值与预测值如表4-3所示。本文用均方根误差(RMSE)、均方误差(MSE)和平均绝对误差(MAE)衡量模型预测效果,结果如表4-4所示。
表4-3 训练集样本真实值与预测值
| 地区 | 真实值 | 预测值 |
| Le Locle | 4.286 | 4.206 |
| St Maurice | 4.174 | 4.286 |
| Rive Droite | 3.78 | 3.951 |
| Sarine | 4.418 | 4.354 |
| Delemont | 4.42 | 4.377 |
| Orbe | 4.05 | 4.192 |
| Monthey | 4.374 | 4.431 |
| Lavaux | 4.176 | 4.173 |
| Gruyere | 4.412 | 4.398 |
表4-4 逐步回归模型预测效果
| 评级指标 | RMSE | MSE | MAE |
|
| 0.089 | 0.008 | 0.074 |
结合表4-3和表4-4可以得出:RMSE为0.089,MSE为0.008,MAE为0.074,说明预测值与真实值相差较小,预测效果很好,反映出逐步回归模型拟合效果非常好。
五、结论及建议
5.1 结论
通过对swiss数据集进行描述性统计分析、建立回归模型、模型诊断与预测,本文得出了如下结论:
- 目前瑞典生育率介于35.00-92.50之间,其平均水平为70.14(平均值)和70.40(中位数);各城市生育率大致服从正态分布,生育率主要集中在60-80之间。
- 瑞典生育率受农业、教育、天主教徒和婴儿死亡率的影响。以对数生育率为因变量建立回归模型比生育率作为因变量建立回归模型效果好。其中婴儿死亡率对生育率的正向影响最大,教育对生育率的负向影响最大。婴儿死亡率每增加一个单位,对数生育率会增加为原来的1.017倍;而教育每增加一个单位,对数生育率会下降为原来的0.984倍。
- 建立逐步回归模型对全模型进行选择时,剔除了变量Examination。逐步回归模型通过自变量共线性检验和模型诊断,模型拟合效果好。以80%样本进行拟合,20%样本进行预测时,均方根误差为0.089,模型预测效果非常好。
5.2 建议
受教育水平的提高,会明显降低生育率,可以考虑为高教育水平人群提供更多生育福利,以增强这群人的生育意愿;农业,也会对生育率产生抑制作用,国家应适当减缓国民经济负担,以提高生育意愿;天主教徒,对生育率具有促进作用,因而可以增强天主教的宣传,增强教会影响力,进而提高生育率。
六、R语言代码
library(faraway)
attach(swiss)
swiss[c(1:5),]
dim(swiss)
swiss$对数Fertility=log(swiss$Fertility)
#描述性统计分析
summary(swiss)
par(mfrow=c(2,3))
hist(Fertility,main="生育率",col='lightblue',xlab="组别" ,ylab = "频数")
hist(Agriculture,main="农业",col='lightblue',xlab="组别" ,ylab = "频数")
hist(Examination,main="审查",col='lightblue',xlab="组别" ,ylab = "频数")
hist(Education,main="教育",col='lightblue',xlab="组别" ,ylab = "频数")
hist(Catholic,main="天主教徒",col='lightblue',xlab="组别" ,ylab = "频数")
hist(Infant.Mortality,main="婴儿死亡率",col='lightblue',xlab="组别" ,ylab = "频数")
#绘制变量之间相关性热力图
library(corrplot)
k=cor(swiss,use='everything',method='pearson')
par(mfrow=c(1,1))
corrplot(k,addCoef.col = "black")
#模型建立
Model.A=lm(Fertility~Agriculture+Examination+Education+Catholic+Infant.Mortality,data=swiss)
summary(Model.A)
Model.B=lm(对数Fertility~Agriculture+Examination+Education+Catholic+Infant.Mortality,data=swiss)
summary(Model.B)
AIC(Model.A,Model.B)
Model.C=step(Model.B,trace=F)#根据AIC准则从全模型Model.A中选出最优子模型,逐步回归
summary(Model.C)#显示模型的各方面细节,包括参数估计值、P值等
anova(Model.B,Model.C)
#共线性检验
library(car)
vif(Model.C)
#模型诊断
par(mfrow = c(2,2))
plot(Model.C,which=1)
plot(Model.C,which = 2)
plot(Model.C,which = 3)
plot(Model.C,which = 4)
#模型预测
len=length(swiss[,1])#样本量
p=0.8#用作训练集的样本概率
ss0=round(len*p)#训练集样本量
swiss1=swiss[order(runif(len)),]
#数据集swiss的前80%作为训练集
A0=swiss1[c(1:ss0),]
#数据集swiss的后20%作为测试集
A1=swiss1[-c(1:ss0),]
Model.BB=lm(对数Fertility~Agriculture+Examination+Education+Catholic+Infant.Mortality,data=A0)
Model.CC=step(Model.BB,trace=F)#根据AIC准则从全模型Model.A中选出最优子模型,逐步回归
summary(Model.CC)#显示模型的各方面细节,包括参数估计值、P值等
pred=predict(Model.CC,A1)
data=data.frame(predict=pred,actual=A1$对数Fertility)
#计算RMSE、MSE、MAE
sqrt(mean((data$predict-data$actual)^2))
mean((data$predict-data$actual)^2)
mean(abs(data$predict-data$actual))个人见解,还请各位读者批评指正!