堆及其实现

news2024/11/19 13:37:28

目录

一：堆的概念及结构

1.概念

2.堆的性质

二：堆的实现

1.堆的构建

2.堆的销毁

3.数据的交换

4.堆的插入

5.堆的判空

6.堆的删除

7.取堆顶的数据   

8.堆的数据个数                         

9.示例

 三：完整的代码

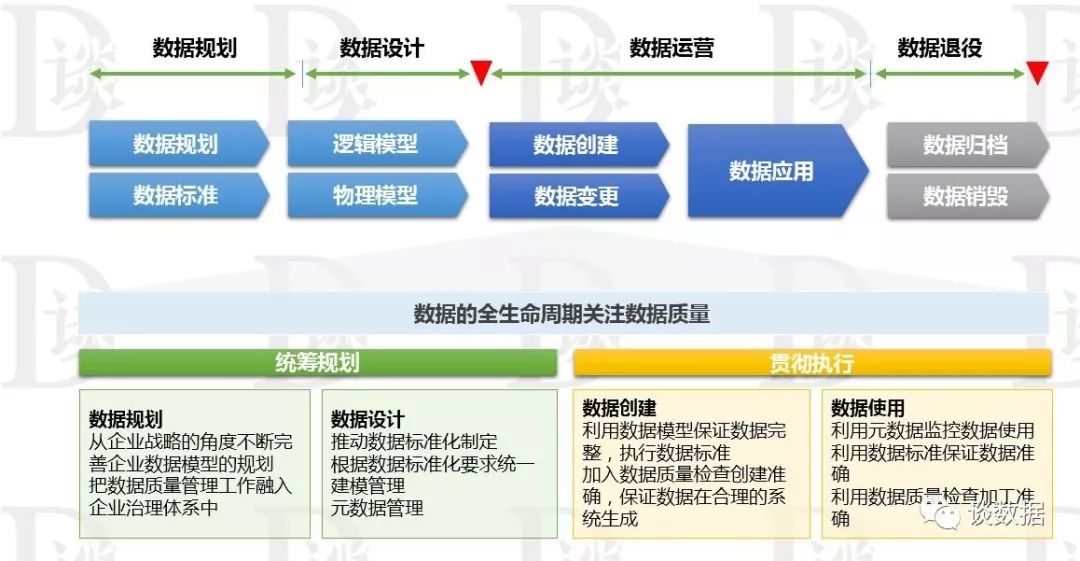
一：堆的概念及结构

1.概念

把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中。
小根堆：每个父亲结点 <= 孩子结点
大根堆：每个父亲结点 >= 孩子结点
72ec17ec1ac04116aca50f35e8b402b7.png

2.堆的性质

<1>.堆中某个节点的值总是不大于或不小于其父节点的值；
<2>.堆总是一棵完全二叉树。
（堆是在完全二叉树的基础上进行了条件限制，可分为：大堆，小堆）

二：堆的实现

 逻辑上为二叉树，但其存储模式为数组。

typedef int HPDataType;//类型重定义

typedef struct Heap
{
    HPDataType* _a;
    int _size;
    int _capacity; 
}Heap;
//逻辑结构为二叉树
//存储结构为数组

1.堆的构建

void HeapCreate(Heap* hp, HPDataType* a, int n);

将数组内容，容量元素个数置为0 --- 初始化

代码为：

// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
	assert(hp);
	hp->_capacity = 0;
	hp->_size = 0;
	hp->_a = NULL;
}

2.堆的销毁

void HeapDestory(Heap* hp);

堆本质是存储在数组中，销毁数组时（其空间是由malloc realloc 开辟而来的），需要free释放掉，free(hp->_a) 。然后将数组，容量，堆内数据个数置为NULL或者0.

代码为：

// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);

	//本质是数组
	free(hp->_a);
	hp->_a = NULL;
	hp->_capacity = 0;
	hp->_size = 0;
}

3.数据的交换

 void Swap(HPDataType* p1, HPDataType* p2)；

在进行向上调整算法，堆的删除，向下调整算法时等时，会存在数据的交换，此时，为了后续更方便使用，我们可以将其分装为一个函数。

//进行数据的交换
void Swap(HPDataType* p1, HPDataType* p2)
{
	//进行数据的交换
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

4.堆的插入

void HeapPush(Heap* hp, HPDataType x);

在插入数据时，需要考虑容量问题 --- 当 hp->_capacity == hp->_size 时，需要开辟空间，或者进行增容，当空间开好后，更新新的数据，数组的空间大小、容量都发生了变化。

进行数据的插入 --- 当数组的数据为 size 个时，其数组对应的下标为 0 - (size-1),所以插入的新的数据的下标为 hp->_size 。然后进行堆内数据 ++ 。

其逻辑结构为二叉树，插入数据后可能需要数据调整，在此处采用向上调整法 --- 需要传入相应的数组，及孩子结点的下标。 --- eg:小根堆

//调整堆 --- 向上调整法

//       数组    孩子的下标 *** 

 AdjustUp(hp->_a,hp->_size-1);

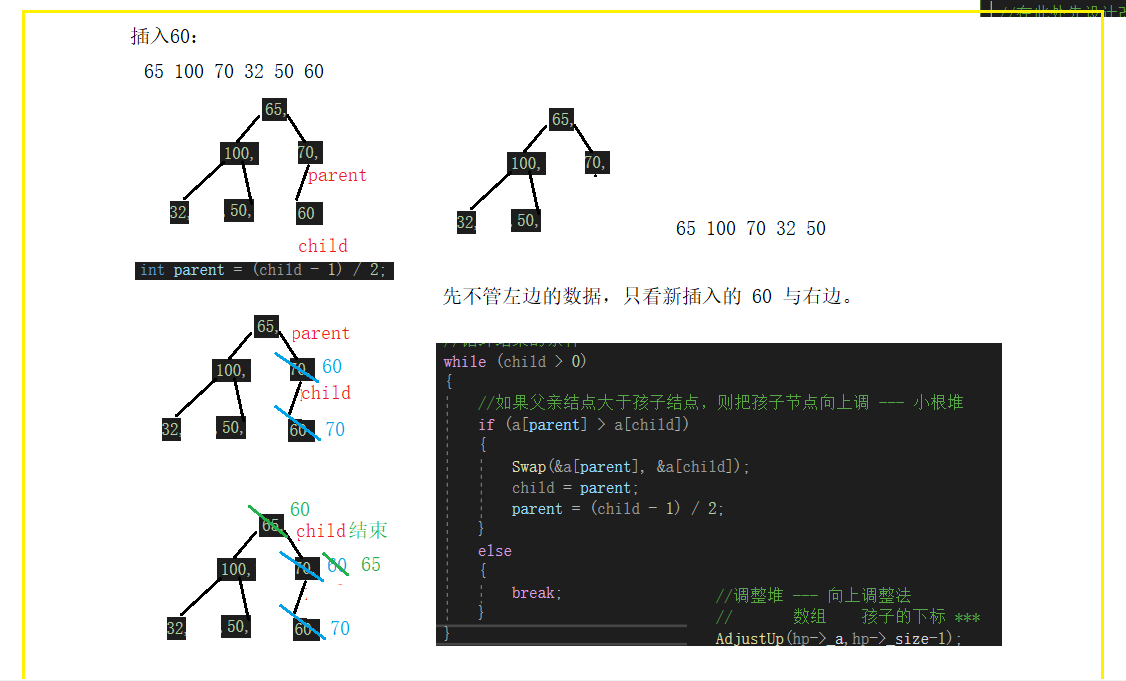
0ff4bd550da447eea99f9611d3ab973d.png

代码为：

//调整堆 --- 向上调整法
//在此处先设计改为小根堆 --- 每个父亲都 <= 孩子 
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
    //循环结束的条件
	while (child > 0)
	{
		//如果父亲结点大于孩子结点，则把孩子节点向上调 --- 小根堆
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

5.堆的判空

 int HeapEmpty(Heap* hp);

在堆删除的过程中，可能会存在，堆内已经没有数据，但是仍在删除的情况，此时肯定会出现错误。当堆内无数据时，则无法进行删除

堆判空的条件为，堆内无数据，即 hp->_size == 0。

 代码为：0

// 堆的判空
int HeapEmpty(Heap* hp)
{
	assert(hp);

	return hp->_size == 0;
}

6.堆的删除

在进行堆的删除的时候，需要进行判断堆内是否为空，若堆内为空，则无法进行删除。

 若堆内有数据，则将首尾元素进行交换，再删除 ，再调堆。 堆删除的前提是左子树和右子树为大堆 / 小堆（此过程在堆的插入时，已经被做好了）

首尾元素进行交换，可以直接使用数据的交换的函数；

在进行数据删除时，可以直接对 hp->_size-- 

再调堆的时候 --- 向下调整算法  需要传入数组，数组的大小，及起初时的父亲结点 （数组下标）。     

画图分析：

代码为：

// 堆的判空
int HeapEmpty(Heap* hp)
{
	assert(hp);

	return hp->_size == 0;
}

//向下调整算法
//在此处先设计改为小根堆 --- 每个父亲都 <= 孩子 
void AdjustDown(int* a, int* n, int parent)
{
	//对其逻辑结构进行分析，如果没有左孩子，则一定没有右孩子
	int child = parent * 2 + 1;//左孩子
	while (child < n)
	{
		//找到左右孩子中的较小孩子 --- 判断右孩子存在
		//                             有左孩子不一定有右孩子 --- 右孩子要先存在，才能与左孩子进行比较，注意写代码时的顺序
		if ( child + 1 < n && a[child] > a[child + 1])//左孩子大于右孩子，则 child 为右孩子，上述假设时，假设的为左孩子小
		{
			++child;
		}

		//找到较小的孩子，与父亲节点进行比较，若比其小，让其与其父亲节点进行交换
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);//让小的节点向上走，大节点向下走
			parent = child;
			child = parent * 2 + 1;//循环更替条件
		}
		else
		{
			break;
		}
	}
}
// 堆的删除
void HeapPop(Heap* hp)  
{
	assert(hp);
	//需要对堆进行判空，若堆为空，则无法进行删除操作
	assert(!HeapEmpty(hp));

	//首尾元素（数据）进行交换，再删除，再调堆
	//前提：左子树和右子树为大堆/小堆
	//采用向下调整法
	
	//交换首尾数据
	Swap(&hp->_a[0], &hp->_a[hp->_size-1]);

	//进行删除
	hp->_size--;

	//调整堆 -- 向下调整 
	AdjustDown(hp->_a, hp->_size, 0);

}

7.取堆顶的数据   

HPDataType HeapTop(Heap* hp);        

需要判断堆是否为空，若堆为空，则无法获取栈顶数据，

又因为在存储结构为数组，所以堆顶数据即为数组下标为0的元素。

代码为：

// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);

	//判断堆是否为空，若为空则无堆顶数据
	assert(!HeapEmpty(hp));

	return hp->_a[0];
}

8.堆的数据个数                         

int HeapSize(Heap* hp);

在插入时，进行了 hp->_size++

在删除时，进行了 hp->_size--

hp->_size 即为堆的数据个数。

代码为：

// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);
	
	return hp->_size;
}

9.示例

#include"Heap.h"

//堆使用的示例
int main()
{
	Heap hp;
	int a[] = { 65,100,70,32,50,60 };
	HeapCreate(&hp, &a, 0);
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
	{
		HeapPush(&hp, a[i]);
	}
	while (!HeapEmpty(&hp))
	{
		int top = HeapTop(&hp);
		printf("%d\n", top);
		HeapPop(&hp);
	}
	return 0;
}

效果为：

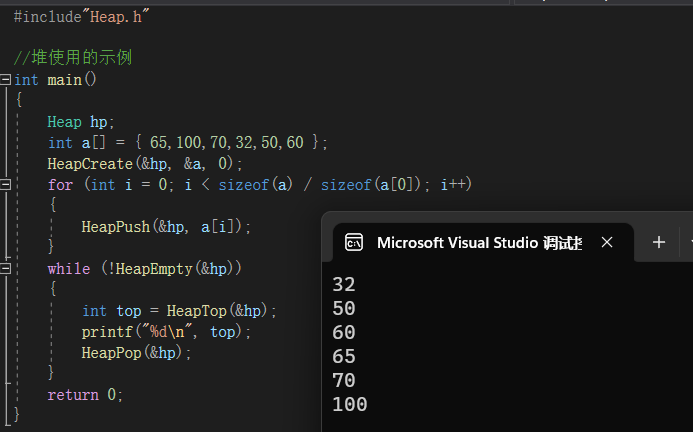
 三：完整的代码

Heap.h

#pragma once

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

typedef int HPDataType;//类型重定义

typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity; 
}Heap;
//逻辑结构为二叉树
//存储结构为数组

// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

Heap.c

#include"Heap.h"


// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
	assert(hp);
	hp->_capacity = 0;
	hp->_size = 0;
	hp->_a = NULL;
}


//进行数据的交换
void Swap(HPDataType* p1, HPDataType* p2)
{
	//进行数据的交换
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


//调整堆 --- 向上调整法
//在此处先设计改为小根堆 --- 每个父亲都 <= 孩子 
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
    //循环结束的条件
	while (child > 0)
	{
		//如果父亲结点大于孩子结点，则把孩子节点向上调 --- 小根堆
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);

	//需要插入新的数据 --- 数组实现
 	if (hp->_capacity == hp->_size)
	{
		int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
		//当空间不够时，需要进行扩容
		//realloc
		//void *realloc( void *memblock, size_t size );
		//              要调整的内存地址 调整之后新的大小
		HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail\n");
			return;
		}
		//空间开好后，更新新的数据
		hp->_a = tmp;
		hp->_capacity = newcapacity;
	}
	//数据的插入，size个元素，下标为 0 - size-1 
	//即新插入的数据的下标为 hp->_size
	hp->_a[hp->_size] = x;
	hp->_size++;

	//调整堆 --- 向上调整法
	//       数组    孩子的下标 ***
	AdjustUp(hp->_a,hp->_size-1);
}

// 堆的判空
int HeapEmpty(Heap* hp)
{
	assert(hp);

	return hp->_size == 0;
}


//向下调整算法
//在此处先设计改为小根堆 --- 每个父亲都 <= 孩子 
void AdjustDown(int* a, int* n, int parent)
{
	//对其逻辑结构进行分析，如果没有左孩子，则一定没有右孩子
	int child = parent * 2 + 1;//左孩子
	while (child < n)
	{
		//找到左右孩子中的较小孩子 --- 判断右孩子存在
		//                             有左孩子不一定有右孩子 --- 右孩子要先存在，才能与左孩子进行比较，注意写代码时的顺序
		if ( child + 1 < n && a[child] > a[child + 1])//左孩子大于右孩子，则 child 为右孩子，上述假设时，假设的为左孩子小
		{
			++child;
		}

		//找到较小的孩子，与父亲节点进行比较，若比其小，让其与其父亲节点进行交换
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);//让小的节点向上走，大节点向下走
			parent = child;
			child = parent * 2 + 1;//循环更替条件
		}
		else
		{
			break;
		}
	}
}
// 堆的删除
void HeapPop(Heap* hp)  
{
	assert(hp);
	//需要对堆进行判空，若堆为空，则无法进行删除操作
	assert(!HeapEmpty(hp));

	//首尾元素（数据）进行交换，再删除，再调堆
	//前提：左子树和右子树为大堆/小堆
	//采用向下调整法
	
	//交换首尾数据
	Swap(&hp->_a[0], &hp->_a[hp->_size-1]);

	//进行删除
	hp->_size--;

	//调整堆 -- 向下调整 
	AdjustDown(hp->_a, hp->_size, 0);

}


// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);
	
	return hp->_size;
}

// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);

	//判断堆是否为空，若为空则无堆顶数据
	assert(!HeapEmpty(hp));

	return hp->_a[0];
}

// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);

	//本质是数组
	free(hp->_a);
	hp->_a = NULL;
	hp->_capacity = 0;
	hp->_size = 0;
}

test.c

#include"Heap.h"

//堆使用的示例
int main()
{
	Heap hp;
	int a[] = { 65,100,70,32,50,60 };
	HeapCreate(&hp, &a, 0);
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
	{
		HeapPush(&hp, a[i]);
	}
	while (!HeapEmpty(&hp))
	{
		int top = HeapTop(&hp);
		printf("%d\n", top);
		HeapPop(&hp);
	}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/562832.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

十、数据仓库详细介绍（数据质量）理论与经验

十、数据仓库详细介绍（数据质量）理论与经验

数据质量管理是对数据从计划、收集、记录、存储、回收、分析和展示生命周期的每个阶段里可能引发的数据质量问题&#xff0c;进行识别、度量、监控、预警等一系列管理活动&#xff0c;并通过改善和提高组织的管理水平使得数据质量获得进一步提高。数据质量管理的终极目标是通过…
阅读更多...
会声会影2023最新完整版免费下载

会声会影2023最新完整版免费下载

会声会影2023操作简单&#xff0c;功能同样强大&#xff01;会声会影附带上百种特效、滤镜、转场、模板。同时各类专业级视频工具&#xff0c;如调色、遮罩、绿幕抠像、运动追踪、分屏创建器&#xff0c;满足更高标准的视频需求。这款软件上手操作简单易学&#xff0c;就算你在…
阅读更多...
Linux之进程管理类命令

Linux之进程管理类命令

进程管理类命令 ps&#xff1a;查看当前系统进程状态 1&#xff09;基本语法 语法说明ps aux查看系统中所有进程ps -ef可以查看父子进程之间的关系 2&#xff09;选项说明 选项说明a列出带有终端的所有用户的进程x列出当前用户的所有进程&#xff0c;包括没有终端的进程u面…
阅读更多...
C语言的一些杂记6

C语言的一些杂记6

实现矩阵序号转置的三种方式 for (i 0; i < row * col; i)t[i / row][i % row] m[i % row][i / row];for (i 0; i < row; i)for (j 0; j < col; j)t[j][i] m[i][j];for (i 0; i < row; i)for (j 0; j < col; j)*(*(t j) i) *(*(m i) j); 变相数组 …
阅读更多...
关于 arduino 中的 map(x, a, b,c,d)函数

关于 arduino 中的 map(x, a, b,c,d)函数

函数名称&#xff1a;map() 包含形参&#xff1a; value&#xff1a;需要映射的值fromLow&#xff1a;输入值的最小值fromHigh&#xff1a;输入值的最大值toLow&#xff1a;输出值的最小值toHigh&#xff1a;输出值的最大值 功能&#xff1a;将一个值从一个范围映射到另一个…
阅读更多...
【环境安装】Linux环境中docker安装redis

【环境安装】Linux环境中docker安装redis

一、找到一个合适的docker的redis的版本 可以去docker hub中去找一下 https://link.juejin.cn/?targethttps%3A%2F%2Fhub.docker.com%2F_%2Fredis%3Ftab%3Dtags 二、使用docker安装redis 我这里安装了具体的某个版本 docker pull redis // 下载最新版Redis镜像 (等同于 : d…
阅读更多...
UAS协议说明

UAS协议说明

1 概述 UAS(USB Attached SCSI)是一种位于SCSI协议框架下传输层的一种协议&#xff0c;其作用是通过基于USB的应用层协议约定&#xff0c;将SCSI的协议数据(Protocol Data Unit)用USB进行封装&#xff0c;从而实现使用USB物理连接进行SCSI协议通信的方式。 UAS实际上定义了两…
阅读更多...
wireshark网络抓包详解

wireshark网络抓包详解

一、简介 Wireshark是一款非常流行的网络封包分析软件&#xff0c;可以截取各种网络数据包&#xff0c;并显示数据包详细信息。 为了安全考虑&#xff0c;wireshark只能查看封包&#xff0c;而不能修改封包的内容&#xff0c;或者发送封包。 wireshark能获取HTTP&#xff0c;也…
阅读更多...
【Android】（最新）跑马灯文字水平滚动（79/100）

【Android】（最新）跑马灯文字水平滚动（79/100）

先上效果&#xff1a; Android系统中TextView实现跑马灯效果&#xff0c;必须具备以下几个条件&#xff1a; android:singleLine“true”android:ellipsize“marquee”android:marqueeRepeatLimit“marquee_forever”TextView必须单行显示&#xff0c;即内容必须超出TextView…
阅读更多...
Jetpack Compose 实现了一个丝滑流畅的页面展开和关闭的效果动画

Jetpack Compose 实现了一个丝滑流畅的页面展开和关闭的效果动画

Jetpack Compose 将动画实现的门槛降低了&#xff0c;不过Compose目前还不支持共享元素过渡。 (上篇文章Jetpack Compose开发的本地笔记本)的动画效果的实现 转跳前的准备工作 定义State枚举类来表示页面的三种状态: Closing(关闭状态) Closed(关闭完成状态) Opening(展开状…
阅读更多...
找不到vcruntime140.dll,无法继续执行代码？多种解决方法解析

找不到vcruntime140.dll,无法继续执行代码？多种解决方法解析

找不到vcruntime140.dll,无法继续执行代码&#xff1f;当你在尝试运行某个程序时&#xff0c;突然弹出一条错误提示框&#xff0c;告诉你无法继续执行代码&#xff0c;因为找不到vcruntime140.dll。这个问题很常见&#xff0c;但是它可能会让你感到困惑和疑惑。这篇文章将详细介…
阅读更多...
chatgpt赋能Python-python_numpy遍历

chatgpt赋能Python-python_numpy遍历

Python NumPy遍历&#xff1a;使用高效的方式为数据科学家节省时间和精力 Python语言在数据科学领域中的地位越来越重要&#xff0c;并成为了数据科学家的首选语言之一。在解决数据问题时&#xff0c;NumPy模块是Python程序员经常使用的一个重要库。NumPy提供了快速的数组操作…
阅读更多...
【大数据实训】—Hadoop开发环境搭建（一）

【大数据实训】—Hadoop开发环境搭建（一）

【大数据实训】—Hadoop开发环境搭建&#xff08;一&#xff09; 第一关、任务描述 本关任务&#xff1a;配置JavaJDK。 相关知识 配置开发环境是我们学习一门IT技术的第一步&#xff0c;Hadoop是基于Java开发的&#xff0c;所以我们学习Hadoop之前需要在Linux系统中配置Jav…
阅读更多...
Flowable钉钉对接005-完成钉钉任务

Flowable钉钉对接005-完成钉钉任务

企业中有自己的业务系统&#xff0c;审批都在业务系统中审批&#xff0c;如何结合移动办公的开放平台实现统一审批至关重要。 场景很简单&#xff0c;自己的系统中可以审批&#xff0c;钉钉上也可以审批&#xff0c;使用H5来适配&#xff0c;统一待办任务 统一待办审批 目标&am…
阅读更多...
python获取tx弹幕数据并制作词云图

python获取tx弹幕数据并制作词云图

前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 知识点介绍: 爬虫基本思路流程 requests模块的使用 pandas读取表格数据 环境介绍: 开发环境: python 3.8 运行代码 pycharm 2022.3 辅助敲代码 模块使用&#xff1a; requests >>> pip install requests pa…
阅读更多...
​年轻人的情绪，都藏在知乎的短故事里

​年轻人的情绪，都藏在知乎的短故事里

“谢邀&#xff0c;与世界分享我刚编的故事。” 这是一句在知乎被调侃的老梗。它源自于知乎上有众多隐匿的大佬&#xff0c;他们经历过各种奇闻轶事&#xff0c;也乐于分享传奇的人生经历&#xff0c;而这其间&#xff0c;很多真假难辨的事迹&#xff0c;也被很多用户笑称可以当…
阅读更多...
这几款好用的软件分享给你

这几款好用的软件分享给你

软件一&#xff1a;Handbrake Handbrake是一款免费开源的视频转码软件&#xff0c;适用于Mac、Windows和Linux系统。它可以将几乎所有视频格式转换为其他格式&#xff0c;包括MP4、MKV、AVI等等。作为一个强大的视频编码器&#xff0c;它可以压缩视频大小&#xff0c;并提供多…
阅读更多...
Android Qcom USB Driver学习(十一)

Android Qcom USB Driver学习(十一)

该系列文章总目录链接与各部分简介&#xff1a; Android Qcom USB Driver学习(零) 基于TI的Firmware Update固件升级的流程分析usb appliction layers的数据 USB Protocol Package ①/② map to check password correct Package Format: Byte[0] Report Id Byte[1] Valid L…
阅读更多...
玩转SpringCloud Alibaba，看阿里大佬的笔记是真香

玩转SpringCloud Alibaba，看阿里大佬的笔记是真香

大家都知道&#xff0c;SpringCloudAlibaba 风靡 Java 开发行业&#xff0c;各个公司都在用这套技术&#xff0c;所以咱们 Java 工程师不管是日常工作或是出去面试&#xff0c;都会用到或者被问到关于SpringCloudAlibaba的应用以及底层原理 所以说&#xff0c;小编下面带来一份…
阅读更多...
用于视频编辑和渲染的最佳GPU是什么？

用于视频编辑和渲染的最佳GPU是什么？

购买新的图形卡&#xff08;GPU&#xff09;可能很困难&#xff0c;尤其是如果涉及您所不熟悉的所有技术问题。 显卡市场上的大多数消费者只需要了解显卡在自己喜欢的游戏中的性能&#xff0c;并确定购买决定即可。但是&#xff0c;如果您想购买GPU进行视频编辑或3D渲染&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023