每日一题

三数之和

题目链接

在这里插入图片描述

思路

解析函数原型

首先我们来看一下题目给的函数原型：
int** threeSum(int* nums, int numsSize, int* returnSize, int**returnColumnSizes)
题目要求我们返回一个二维数组，数组的行数代表着存在多少个满足条件的三元组，而在本题中，列数规定为3，即每行存储3个元素
在螺旋矩阵中我们已经做过分析，nums就是题目给的整数数组，numsSize就是这个数组的大小，returnSize就是我们返回的二维数组的行数，returnColumnSizes是一个一维数组，它储存的就是我们返回的二维数组的每一行的列数。

整体框架

这一题其实就是昨天两数之和拓展部分的进阶版，在《两数之和》中我们提到，如果题目要求我们返回的是满足条件的三个元素的数值，那我们就可以采用双指针的办法来解决问题

而使用双指针的前提条件，就是要确保数组是有序的，因为只有这样，才能保证left右移时，sum变大，right左移时sum变小，因此我们第一步就是要对数组进行排序
那么具体的，我们怎么使用双指针这一方法呢？
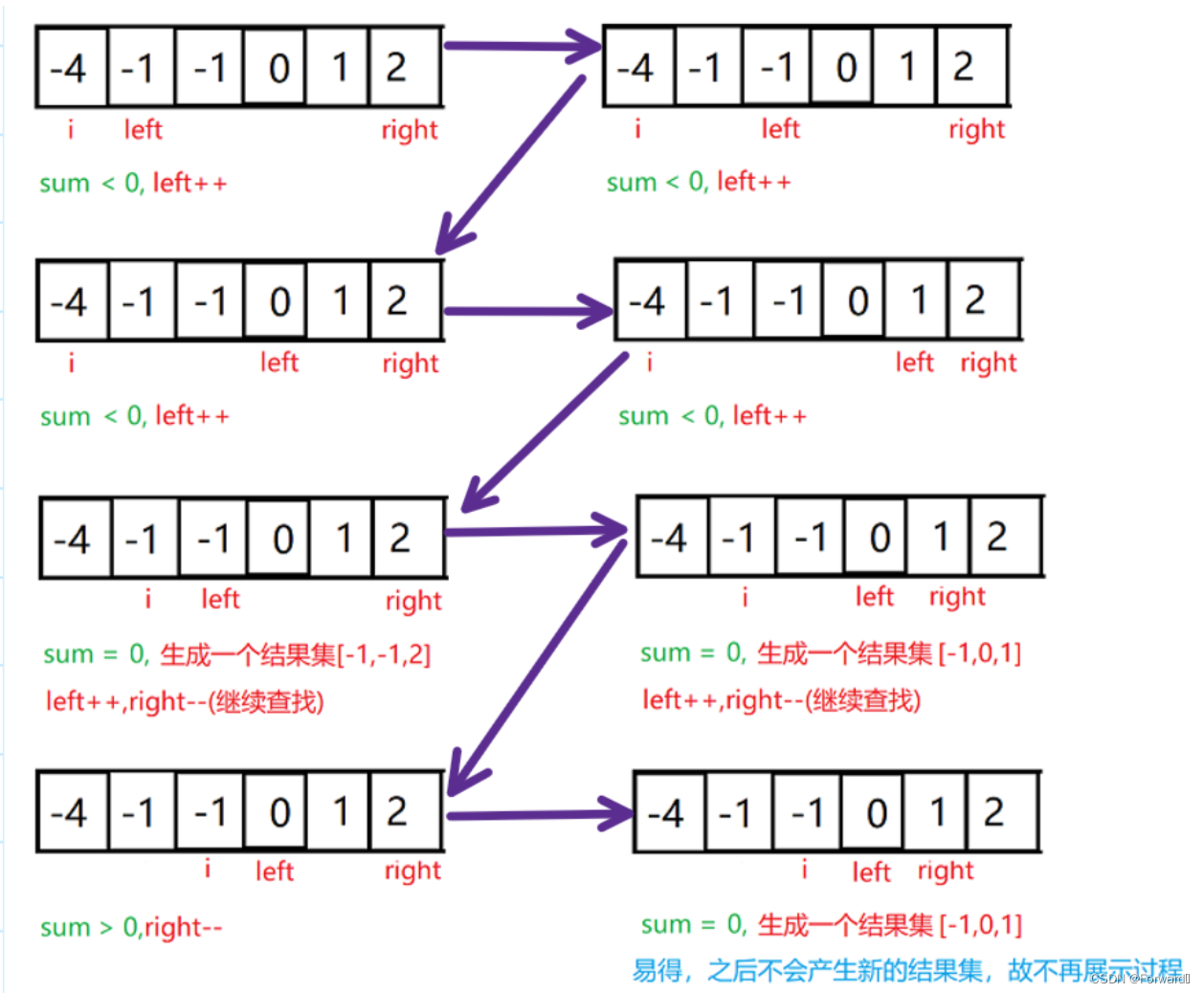
首先利用一层循环，来遍历整个数组
for(int i = 0; i < numsSize; i++)
{
    ………………;
}
然后我们用left指向i的后一个元素，right指向数组nums的最后一个元素，这里我们令nums[i] = a, nums[left] = b, nums[right] = c, sum = a + b + c
接下来，就和《两数之和》里的方法类似了，如果sum > 0，那么right–，如果sum < 0，那么lerft++，如果sum == 0，那么就将a，b，c这三个数存入结果数组中
for(i = 0; i < numsSize; i++)
{
    int left = i + 1;
    int right = numsSize - 1;
    while(left < right)
    {
        int sum = nums[i] + nums[left] + nums[right];
        if(sum > 0)
            right--;
        else if(sum < 0)
            left++;
        else
        {
			//存入数据
        }
    }
}
过程如图：

去重

可以看到，这一个例子的结果集为{{-1,-1,2},{-1,0,1},{-1,0,1}}，但是题目要求，答案中不能包含重复的三元组，因此我们还要考虑去重的问题
a（nums[i]）的去重：
由于数组有序，且a是遍历数组的值，因此a便不允许重复出现

那么我们是要判断nums[i] == nums[i + 1]还是判断nums[i] == nums[i - 1]呢？

假设给定的数组为{-1,-1,2}，如果我们用if(nums[i] == nums[i + 1])进行判断，那么第一个-1就会被跳过，这个三元组就不会被计入到结果集中，显然这是不合理的

而用if(nums[i] == nums[i - 1)进行判断就不会出现这种情况
为什么会出现这种情况？我们要清楚题目要求的是不能出现重复的三元组，而不是三元组中不能出现重复的元素，如果用第ifif(nums[i] == nums[i + 1])判断，那么就会将三元组中出现重复元素这一情况给排除，不合题意
if(i > 0 && nums[i] == nums[i - 1])		//加上i > 0是为了防止数组越界访问
    continue;
b（nums[left]），c（nums[right]）的去重
当我们执行left++，right- -操作的时候，如果nums[left] == nums[++left]，或nums[right] == nums[- -right]，那么显然也会出现重复的情况，因此当出现相等时，我们就要继续++left，或- -right
while(left < right && nums[right] == nums[--right]);
while(left < right && nums[left] == nums[++left]);

//也可以写为
/*
while(left < right && nums[right] == nums[right - 1])
	right--;
while(left < right && nums[left] == nums[left + 1])
	left++;
*/

实现代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 //将数组从小到大排序
void Sort(int *nums, int numsSize)
{
    for(int i = 0; i < numsSize - 1; i++)
    {
        for(int j = i + 1; j < numsSize; j++)
        {
            if(nums[i] > nums[j])
            {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
            }
        }
    }
}
int** threeSum(int* nums, int numsSize, int* returnSize, int**returnColumnSizes){
    int base = 100;     //假设有100组数
    
    //申请内存
    int **arr = (int **)malloc(sizeof(int *) * base);	
    *returnColumnSizes = (int *)malloc(sizeof(int) * base);	
    
    //三元组的个数初始化为0
    *returnSize = 0;
    
    Sort(nums,numsSize);    //将数组从小到大排序
    
    //如果最小的数都大于0，那么直接返回空数组
    if(nums[0] > 0)
        return NULL;
    
    //开始寻找符合条件的三元组
    int i = 0;
    for(i = 0; i < numsSize; i++)
    {
        //a的去重
        if(i > 0 && nums[i] == nums[i - 1])
            continue;
        
        int left = i + 1;
        int right = numsSize - 1;
        
        //双指针查找
        while(left < right)
        {
            int sum = nums[i] + nums[left] + nums[right];
            if(sum > 0)
                right--;
            else if(sum < 0)
                left++;
            //如果找到符合条件的三个数
            else
            {
                (*returnColumnSizes)[(*returnSize)] = 3;	//将存储第(*returnSize)组三元组的数组的行数确定为3
                //申请存储第(*returnSize)组三元组的数组的内存
                arr[(*returnSize)] = (int *)malloc(sizeof(int) * 3);	
                
                //将数据存入数组
                arr[(*returnSize)][0] = nums[i];
                arr[(*returnSize)][1] = nums[left];
                arr[(*returnSize)][2] = nums[right];
                
                //三元组个数加一
                (*returnSize)++;
                
                //实现b，c去重
                while(left < right && nums[right] == nums[--right]);
                while(left < right && nums[left] == nums[++left]);
                //也可以写成这样
                /*
                while(left < right && nums[right] == nums[right - 1])
                    right--;
                while(left < right && nums[left] == nums[left + 1])
                    left++;
                right--;
                left++;
                */
            }
            
            //如果三元组个数等于初始值base，那么就要进行扩容
            if((*returnSize) == base)
            {
                base *= 2; 
                arr = (int **)realloc(arr,sizeof(int *) * base);
                *returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * base);
            }
        }
    }
    
    //返回最终的结果集
    return arr;
}